28.1锐角三角函数-九年级数学人教版（下）（解析版）.doc

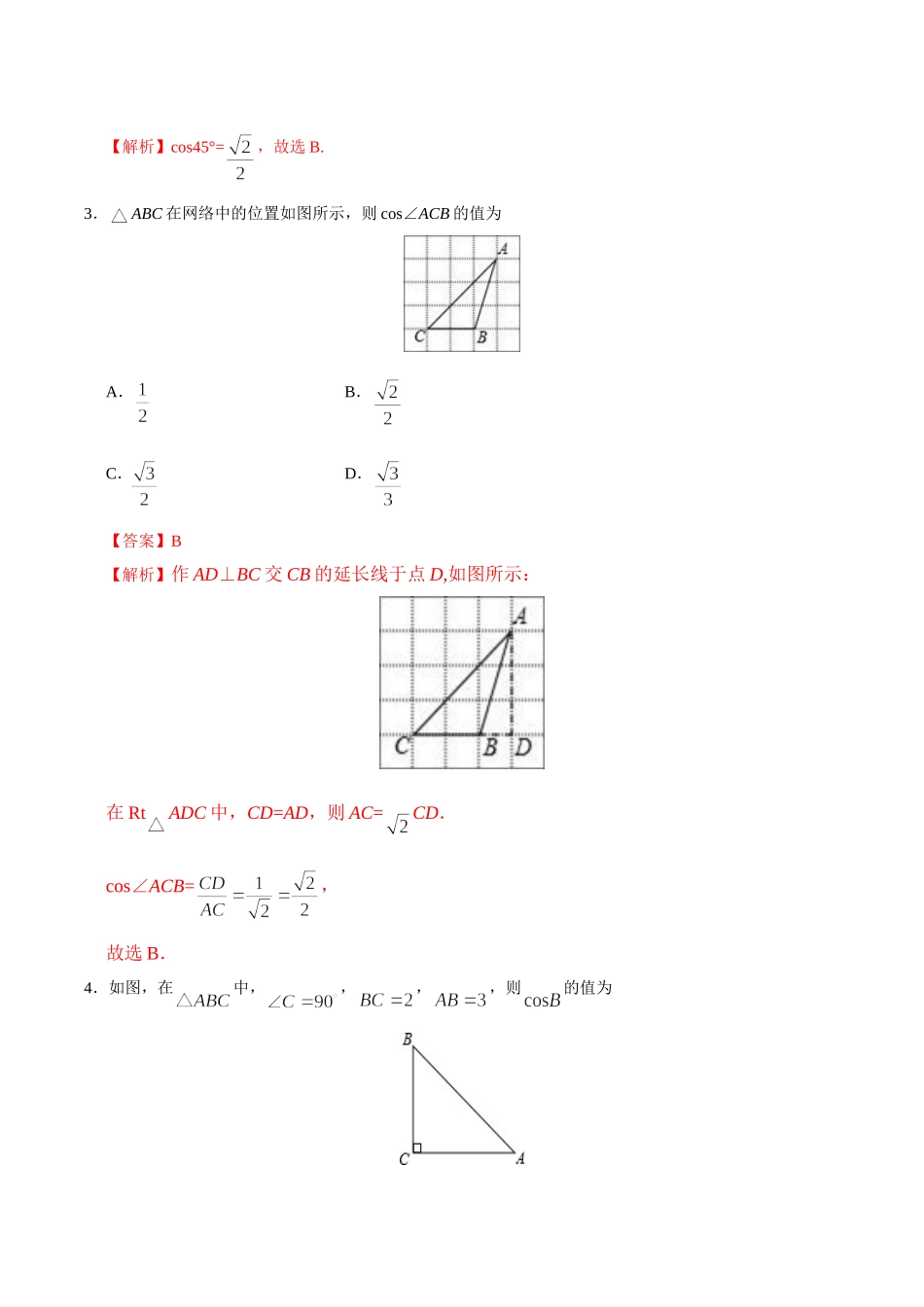
第二十八章 锐角三角函数 28.1 锐角三角函数 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．如图，在6×4的正方形网格中，ABC的顶点均为格点，则sin∠ACB= A． B．2 C． D． 【答案】C 【解析】如图所示， ∵BD=2，CD=1， ∴BC===， 则sin∠BCA===， 故选：C． 2．cos45°的值等于 A． B． C． D．1 【答案】B 【解析】cos45°=，故选B. 3．ABC在网络中的位置如图所示，则cos∠ACB的值为 A． B． C． D． 【答案】B 【解析】作AD⊥BC交CB的延长线于点D,如图所示： 在RtADC中，CD=AD，则AC=CD． cos∠ACB=， 故选B． 4．如图，在中，，，，则的值为 A． B． C． D． 【答案】A 【解析】cosB= ,故选A． 5．在中，，若，则的值是 A． B． C． D． 【答案】D 6．在RtABC中，∠C＝90°，AC＝12，BC＝5，那么tanA等于 A． B． C． D． 【答案】C 【解析】∵在RtABC中，∠C=90°，AC=12，BC=5，∴tanA==． 故选：C． 7．在RtABC中，∠C=90°， AB=10， AC=8，则∠A的正弦值等于 A． B． C． D． 【答案】A 【解析】∵AB=10， AC=8， ∴BC=， ∴sinA=. 故选A. 【名师点睛】本题考查了勾股定理和锐角三角函数的概念，熟练掌握锐角三角函数的定义是解答本题的关键.在RtABC中， ， ，. 8．把ABC的各边长都增加两倍，则锐角A的正弦值 A．增加2倍 B．增加4倍 C．不变 D．不能确定 【答案】C 9．如图，在平面直角坐标系中，点A的坐标为（3,4），那么sin的值是 A． B． C． D． 【答案】C 【解析】作AB⊥x轴交x轴于点B， ∵A（3，4）， ∴AB=4，BO=3， ∴AO===5， ∴sin==. 故选C. 【名师点睛】要求一个角的三角函数值，如果图中没有现成的直角三角形，我们一般通过构造垂线将要求的角放入直角三角形中求解. 10．如图，ABC的三个顶点分别在正方形网格的格点上，则tanC的值是 A． B． C． D． 【答案】A 【解析】如图，tanC==． 故选A． 【名师点睛】本题考查了锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边． 二、填空题：请将答案填在题中横线上． 11．如图，P为∠α的边OA上一点，且P点的坐标为（3，4），则sinα+cosα=________． 【答案】 【解析】∵P是∠α的边OA上一点，且P点坐标为（3，4）， ∴PB=4，OB=3，OP= =5, 故sinα= = , cosα= , ∴sinα+cosα=, 故答案为：. 【名师点睛】此题考查的是锐角三角函数的定义，解答此类题目的关键是找出所求角的对应边． 12．计算：sin30°﹣（﹣3）0=________． 【答案】− 【解析】原式=−1=−，故答案为：−. 【名师点睛】本题考查了30°的角的正弦值和非零数的零次幂.熟记是关键. 13．在中，，，，则________，________． 【答案】 【解析】如图： ∵RtABC中，∠C=90°，AC=12，AB=13， ∴BC==5， ∴cosB=， tanB=． 故答案为：；． 【名师点睛】本题考查锐角三角函数的定义：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边． 14．在ABC中，若+，则∠C的度数为___________. 【答案】105° 【名师点睛】本题考查了特殊角的三角函数值，难度一般，解答本题的关键是根据题意得出tanA=1，cosB=，求出∠A、∠B的值． 三、解答题：解答应写出文字说明、证明过程或演算步骤． 15．计算：÷+8×2﹣1﹣（+1）0+2•sin60°． 【解析】原式=+8×﹣1+2×=3+4﹣1+=6+． 【名师点睛】本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍． 16．先化简，再求代数式（）÷的值，其中x=sin60°，y=tan30°． 【解析】原式 ∴原式 17．定义概念：如图，在直角三角形ABC中，锐角α的对边与斜边的比叫做角α的正弦，记作sinα，即sinα=，根据上述角的正弦的概念，解答下列问题：在RtABC中， （1）当AC=12，AB=13时，求sinα的值； （2）当α=30°，AB=20时，则BC=　 　． 【解析】（1）∵AC=12，AB=13，∠BCA=90°， ∴BC=5， ∴sinα （2）∵AB=20，∠BCA=90°，α=30°， ∴BC=10； 故答案为：10．