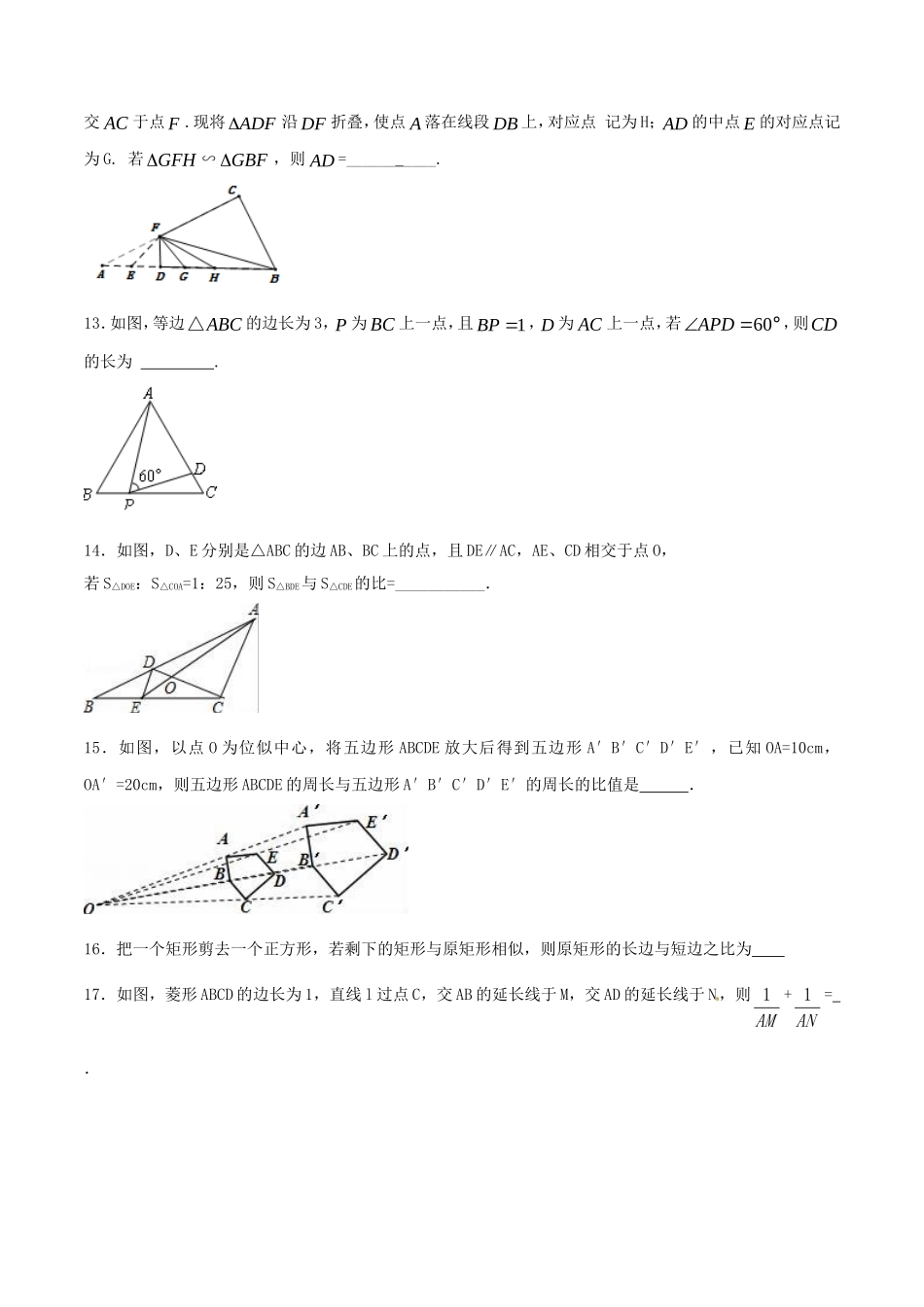
《第二十七章相似》测试卷(A卷)(测试时间:120分钟满分:120分)一、选择题(每小题3分,共30分)1.已知:线段a、b,且,则下列说法错误的是()A.a=2cm,b=3cmB.a=2k,b=3k(k≠0)C.3a=2bD.2.下列命题正确的是()A.有一个角对应相等的平行四边形都相似B.对应边成比例的两个平行四边形相似C.有一个角对应相等的两个等腰梯形相似D.有一个角对应相等的菱形是相似多边形3.如果(其中顶点、、依次与顶点、、对应),那么下列等式中不一定成立的是()A.B.∠B=∠EC.D.4.在比例尺为1∶8000的某学校地图上,矩形运动场的图上尺寸是1cm×2cm,那么矩形运动场的实际尺寸应为()A.80m×160mB.8m×16mC.800m×160mD.80m×800m5.如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是()A.(-1,2)B.(-9,18)C.(-9,18)或(9,-18)D.(-1,2)或(1,-2)6.如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有()A.1对B.2对C.3对D.4对7.已知:如图,在中,,则下列等式成立的是()A.B.C.D.8.如图,在平行四边形中,是上的一点,直线与的延长线交于点,并与交于点,下列式子中错误的是()[来源:Zxxk.Com]A.B.C.D.9.如图,在中,是边上一点,连接,给出下列条件:①;②;③;④.其中单独能够判定的个数是()A.1个B.2个C.3个D.4个10.点是线段的黄金分割点,且,下列命题:,中正确的有()A.1个B.2个C.3个D.4个[来源:学+科+网]二、填空题(每小题3分,共30分)11.如图,在△ABC中,DE∥BC,23ADDB,则DEBC=.12.如图,直角三角形ABC中,90ACB,10AB,6BC,在线段AB上取一点D,作ABDF交AC于点F.现将ADF沿DF折叠,使点A落在线段DB上,对应点记为H;AD的中点E的对应点记为G.若GFH∽GBF,则AD=__________.13.如图,等边ABC△的边长为3,P为BC上一点,且1BP,D为AC上一点,若60APD°,则CD的长为.14.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比=___________.15.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是.16.把一个矩形剪去一个正方形,若剩下的矩形与原矩形相似,则原矩形的长边与短边之比为17.如图,菱形ABCD的边...