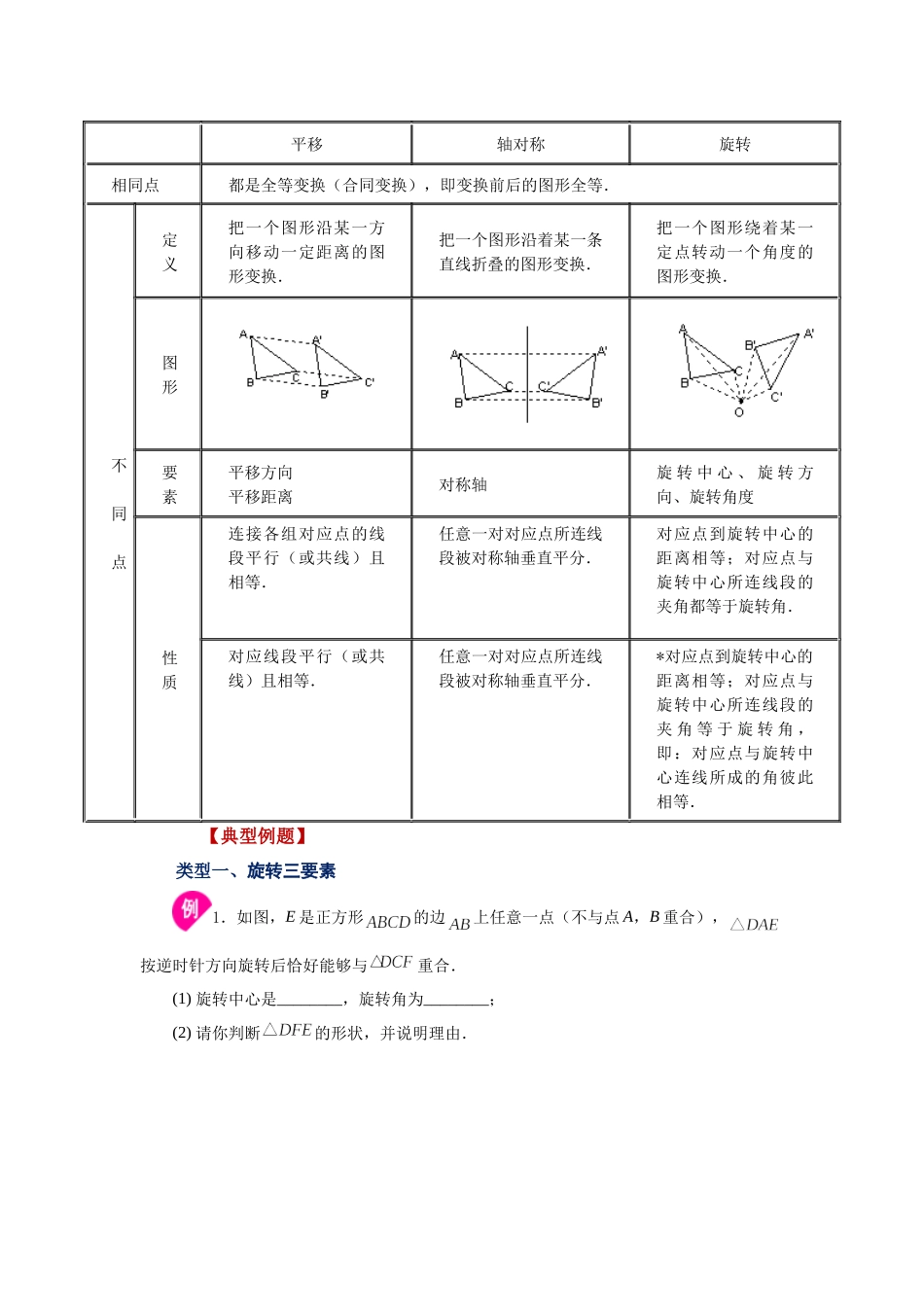
专题23.7《旋转》全章复习与巩固(知识讲解)【学习目标】1、通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质;2、通过具体实例认识中心对称,探索它的基本性质,理解对应点所连线段被对称中心平分的性质,了解平行四边形、圆是中心对称图形;3、能够按要求作出简单平面图形旋转后的图形,欣赏旋转在现实生活中的应用;4、探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用轴对称、平移和旋转的组合进行图案设计.【要点梳理】要点一、旋转1.旋转的概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转..点O叫做旋转中心,转动的角叫做旋转角(如∠AOA′),如果图形上的点A经过旋转变为点A′,那么,这两个点叫做这个旋转的对应点.特别说明:旋转的三个要素:旋转中心、旋转方向和旋转角度.2.旋转的性质:(1)对应点到旋转中心的距离相等(OA=OA′);(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前、后的图形全等(△ABC≌△).特别说明:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.3.旋转的作图:在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.作图的步骤:(1)连接图形中的每一个关键点与旋转中心;(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;(4)连接所得到的各对应点.要点二、特殊的旋转—中心对称1.中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.特别说明:(1)有两个图形,能够完全重合,即形状大小都相同;(2)位置必须满足一个条件:将其中一个图形绕着某一个点旋转180°能够与另一个图形重合(全等图形不一定是中心对称的,而中心对称的两个图形一定是全等的).2.中心对称图形:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.特别说明:(1)中心对称图形指的是一个图形;(2)线段,平行四边形,圆等等都是中心对称图形.要点三、平移、轴对称、旋转平移、轴对称、旋转之间的对比平移轴对称旋转相同点都是...