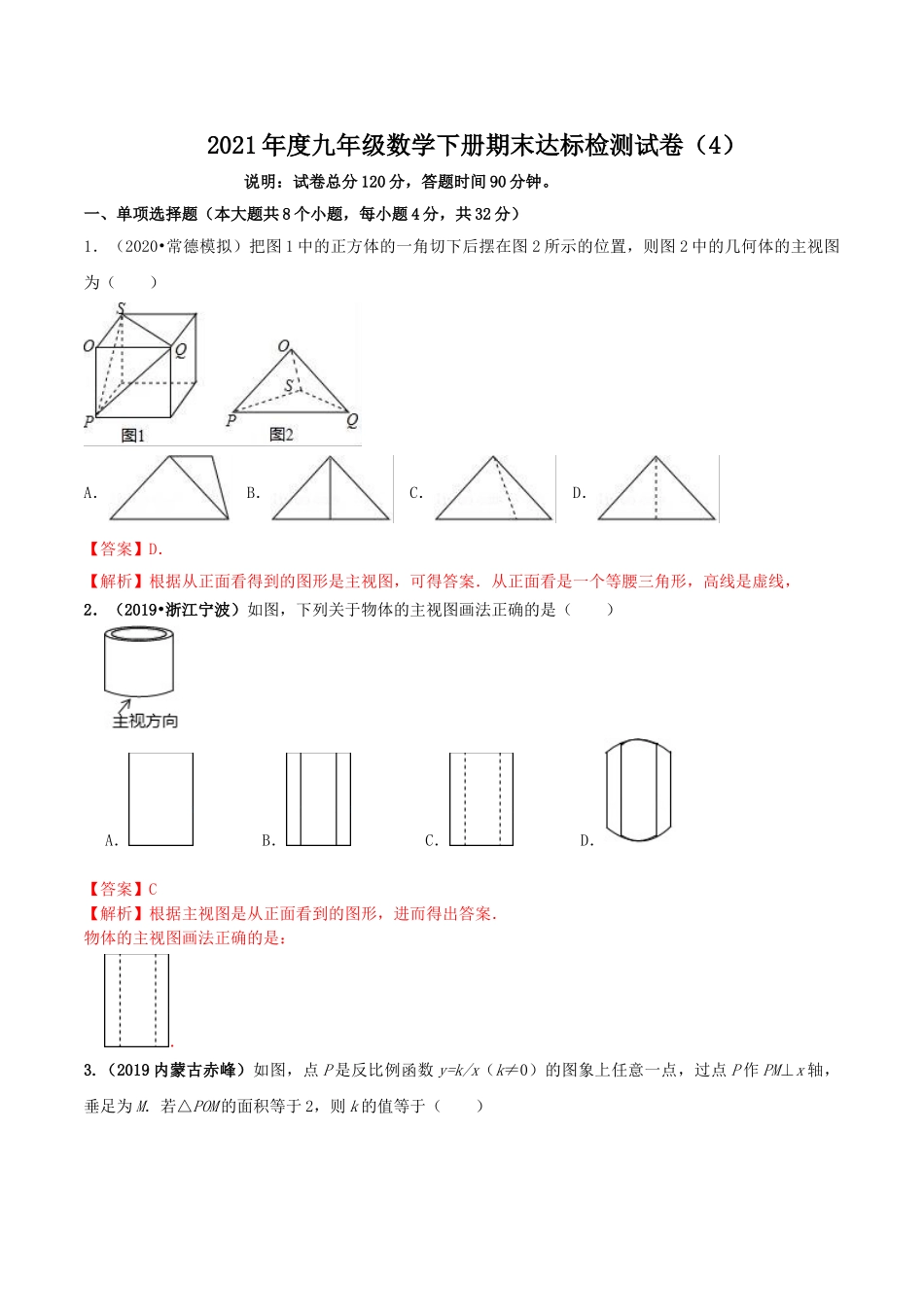
2021年度九年级数学下册期末达标检测试卷(4)说明:试卷总分120分,答题时间90分钟。一、单项选择题(本大题共8个小题,每小题4分,共32分)1.(2020•常德模拟)把图1中的正方体的一角切下后摆在图2所示的位置,则图2中的几何体的主视图为()A.B.C.D.【答案】D.【解析】根据从正面看得到的图形是主视图,可得答案.从正面看是一个等腰三角形,高线是虚线,2.(2019•浙江宁波)如图,下列关于物体的主视图画法正确的是()A.B.C.D.【答案】C【解析】根据主视图是从正面看到的图形,进而得出答案.物体的主视图画法正确的是:.3.(2019内蒙古赤峰)如图,点P是反比例函数y=k/x(k≠0)的图象上任意一点,过点P作PM⊥x轴,垂足为M.若△POM的面积等于2,则k的值等于()A.﹣4B.4C.﹣2D.2【答案】A【解析】 △POM的面积等于2,∴|k|=2,而k<0,∴k=﹣4.4.(2019四川泸州)如图,一次函数y1=ax+b和反比例函数y2=k/x的图象相交于A,B两点,则使y1>y2成立的x取值范围是()A.﹣2<x<0或0<x<4B.x<﹣2或0<x<4C.x<﹣2或x>4D.﹣2<x<0或x>4【答案】B【解析】观察函数图象可发现:当x<﹣2或0<x<4时,一次函数图象在反比例函数图象上方,∴使y1>y2成立的x取值范围是x<﹣2或0<x<4.故选:B.5.(2019湖北十堰)如图,平面直角坐标系中,A(﹣8,0),B(﹣8,4),C(0,4),反比例函数y=k/x的图象分别与线段AB,BC交于点D,E,连接DE.若点B关于DE的对称点恰好在OA上,则k=()A.﹣20B.﹣16C.﹣12D.﹣8【答案】C【解析】根据点的坐标可得矩形的长和宽,易知点D的横坐标,E的纵坐标,由反比例函数的关系式,可用含有k的代数式表示另外一个坐标,由三角形相似和对称,可求出AF的长,然后把问题转化到三角形ADF中,由勾股定理建立方程求出k的值.解:过点E作EG⊥OA,垂足为G,设点B关于DE的对称点为F,连接DF、EF、BF,如图所示:则△BDE≌△FDE,∴BD=FD,BE=FE,∠DFE=∠DBE=90°易证△ADF∽△GFE∴, A(﹣8,0),B(﹣8,4),C(0,4),∴AB=OC=EG=4,OA=BC=8, D、E在反比例函数y=k/x的图象上,∴E(k/4,4)、D(﹣8,-k/8)∴OG=EC=-k/4,AD=-k/8,∴BD=4+k/8,BE=8+k/8∴,∴AF=EG/2=2,在Rt△ADF中,由勾股定理:AD2+AF2=DF2即:(-k/8)2+22=(4+k/8)2解得:k=﹣126.(2020•重庆模拟)已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为()A.1:4B.4:1C.1...