28.2 解直角三角形同步练习4 新人教版.docVIP免费

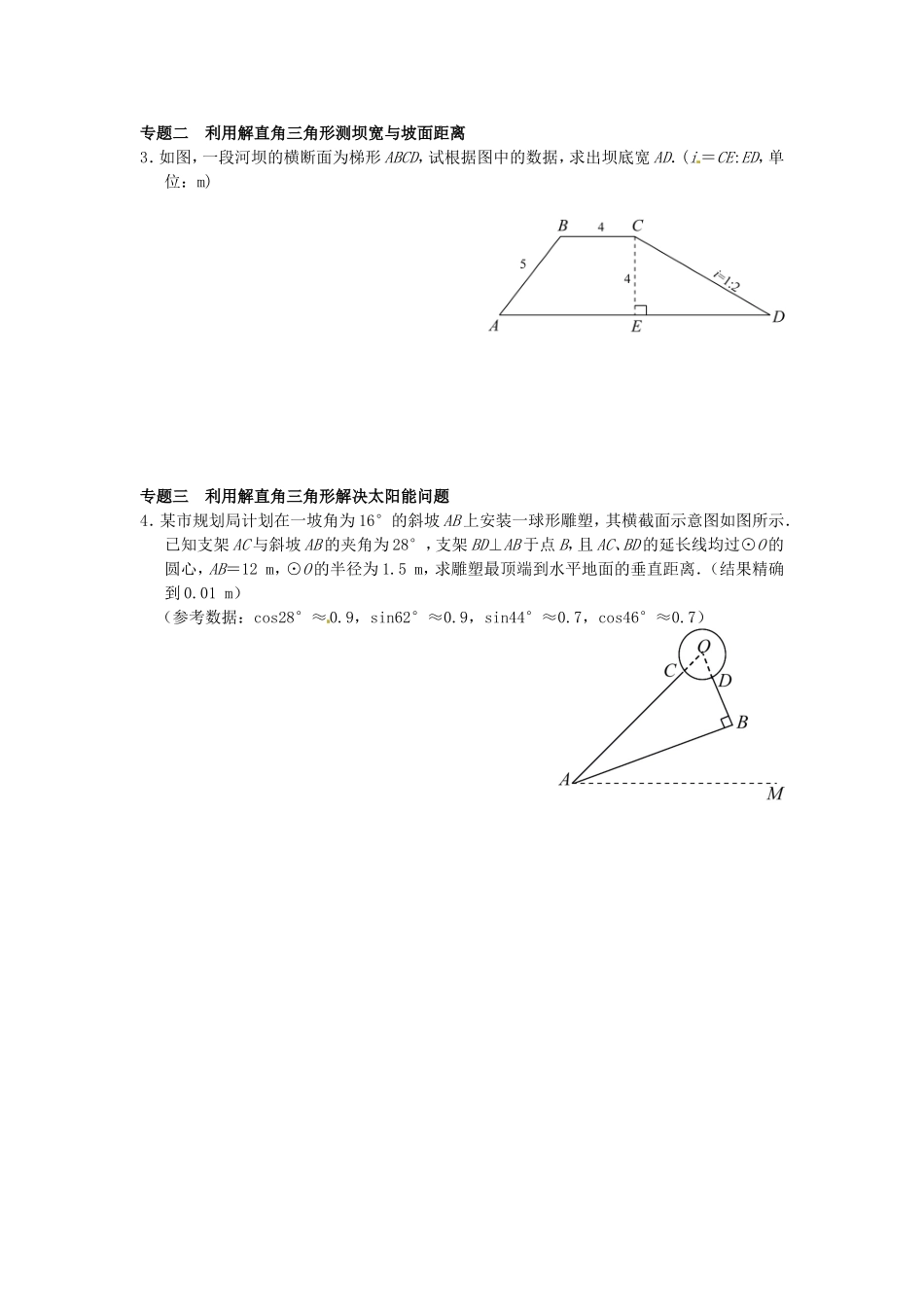
28.2解直角三角形专题一利用解直角三角形测河宽与山高1．如图，小丽想知道自家门前小河的宽度，于是她按以下办法测出了如下数据：小丽在河岸边选取点A，在点A的对岸选取一个参照点C，测得∠CAD＝30°；小丽沿河岸向前走30m选取点B,并测得∠CBD＝60°.请根据以上数据,用你所学的数学知识,帮助小丽计算小河的宽度.2．在一次暑假旅游中，小亮在仙岛湖的游船上（A处），测得湖西岸的山峰太婆尖（C处）和湖东岸的山峰老君岭（D处）的仰角都是45°，游船向东航行100米后（B处），测得太婆尖、老君岭的仰角分别为30°、60°．试问太婆尖、老君岭的高度为多少米？（3≈1.732，结果精确到1米）专题二利用解直角三角形测坝宽与坡面距离3．如图，一段河坝的横断面为梯形ABCD，试根据图中的数据，求出坝底宽AD．(i＝CE:ED，单位：m)专题三利用解直角三角形解决太阳能问题4．某市规划局计划在一坡角为16°的斜坡AB上安装一球形雕塑，其横截面示意图如图所示．已知支架AC与斜坡AB的夹角为28°，支架BD⊥AB于点B，且AC、BD的延长线均过⊙O的圆心，AB＝12m，⊙O的半径为1.5m，求雕塑最顶端到水平地面的垂直距离．（结果精确到0.01m）（参考数据：cos28°≈0.9，sin62°≈0.9，sin44°≈0.7，cos46°≈0.7）【知识要点】１.解直角三角形的几种基本图形：图形1：tan30°＝33axx，∠ABD＝∠A，BD＝AD＝a，tan60°＝xxa，xax333，2360sinax，xax3，213xa．ax23.aax21313.图形2：tan30°＝33xax，tan60°＝3xax，aax21313．aax233133.图形3：AC＝CD＝a＋x，AC＝BE＝DE＝x,∠BAD＝∠BDA＝30°,tan30°＝33axx，tan60°＝3xxa,AB＝BD＝a，aax21313.aax21313.x＝21BD＝21a.【温馨提示】１.解直角三角形的基本思想是“化斜为直”，在转化过程中，尽量保证已知度数的角的完整性.２.当一个三角形是钝角三角形，且其钝角的补角是30、45、60度时，常常从该钝角顶点向对边作垂线构造“双直角三角形”.【方法技巧】１.双直角三角形中，公共直角边是“桥梁”，通过它建立起两直角三角形的联系.２.如果条件中给出参考数据，结合原始数据，构造直角三角形.当计算过程中用到了参考数据，你的思路一定是正确的.参考答案1．解：示意图如下：连接AC，BC，过点C作CE⊥AD于E.由题意得，∠ACB＝∠CBE－∠CAD=60°－30°＝30°，∴∠CAD＝∠ACB，∴BC＝AB＝30.在Rt△BEC中，CE＝BCsin60°＝30×23＝153（m...