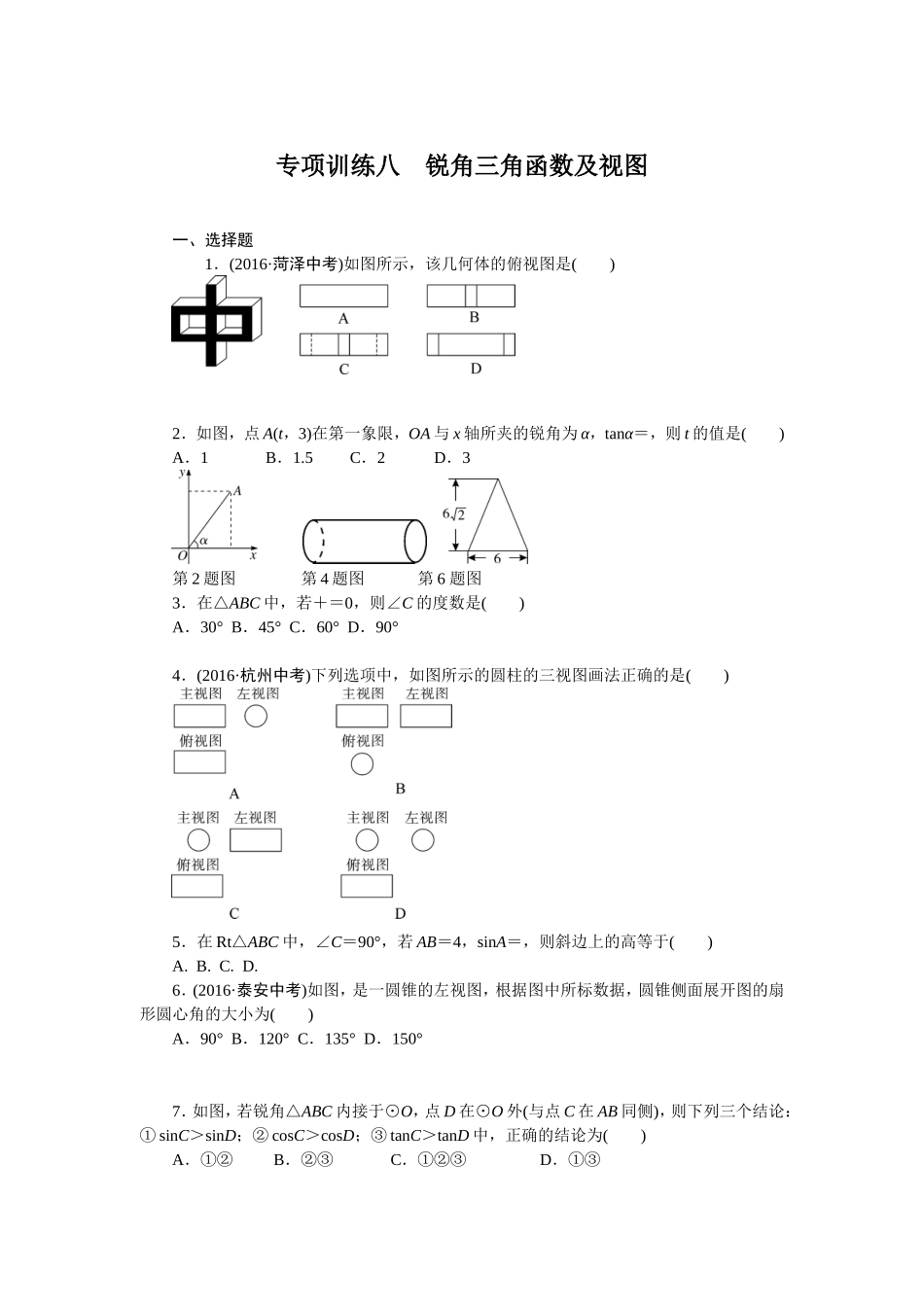
专项训练八　锐角三角函数及视图.doc

专项训练八　锐角三角函数及视图 一、选择题 　　1．(2016·菏泽中考)如图所示，该几何体的俯视图是(　　) 2．如图，点A(t，3)在第一象限，OA与x轴所夹的锐角为α，tanα＝，则t的值是(　　) A．1 B．1.5 C．2 D．3 第2题图 第4题图 第6 题图 3．在△ABC中，若＋＝0，则∠C的度数是(　　) A．30° B．45° C．60° D．90° 4．(2016·杭州中考)下列选项中，如图所示的圆柱的三视图画法正确的是(　　) 5．在Rt△ABC中，∠C＝90°，若AB＝4，sinA＝，则斜边上的高等于(　　) A. B. C. D. 6．(2016·泰安中考)如图，是一圆锥的左视图，根据图中所标数据，圆锥侧面展开图的扇形圆心角的大小为(　　) A．90° B．120° C．135° D．150° 　　　 7．如图，若锐角△ABC内接于⊙O，点D在⊙O外(与点C在AB同侧)，则下列三个结论：①sinC＞sinD；②cosC＞cosD；③tanC＞tanD中，正确的结论为(　　) A．①② B．②③ C．①②③ D．①③ 第7题图 第8 题图 8．如图①，某超市从一楼到二楼有一自动扶梯，图②是侧面示意图．已知自动扶梯AB的坡度为1∶2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，则二楼的层高BC约为(精确到0.1米，sin42°≈0.67，tan42°≈0.90)(　　) A．10.8米 B．8.9米 C．8.0米 D．5.8米 二、填空题 9． 如图，Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，则AB的长为________． 第9 题图 第11题图 　第12题图 10．在△ABC中，∠A，∠B都是锐角，若sinA＝，cosB＝，则∠C＝________． 11．如图，已知AB是⊙O的直径，弦CD⊥AB，AC＝2，BC＝1，那么cos∠ABD的值是________． 12．(2016·昆山市二模)如图，在菱形ABCD中，DE⊥AB，cosA＝，BE＝2，则tan∠DBE＝________. 13．某校研究性学习小组测量学校旗杆AB的高度，如图，在教学楼一楼C处测得旗杆顶部的仰角为60°，在教学楼三楼D处测得旗杆顶部的仰角为30°，旗杆底部与教学楼一楼在同一水平线上，已知每层楼的高度为3米，则旗杆AB的高度为______米． 第13 题图 第14 题图 14．(2016·大庆中考)由若干棱长相等的小正方体构成的几何体的主视图、左视图、俯视图如图所示，则构成这个几何体的小正方体有________个． 三、解答题 15．在△ABC中，AD是BC边上的高，∠C＝45°，sinB＝，AD＝1.求BC的长． 16．(2016·荆门中考)如图，天星山山脚下西端A处与东端B处相距800(1＋)米，小军和小明同时分别从A处和B处向山顶C匀速行走．已知山的西端的坡角是45°，东端的坡角是30°，小军的行走速度为米/秒．若小明与小军同时到达山顶C处，则小明的行走速度是多少？ 17．有一个几何体的形状为直三棱柱，右图是它的主视图和左视图． (1)请补画出它的俯视图，并标出相关数据； (2)根据图中所标的尺寸(单位：厘米)，计算这个几何体的全面积． 18．(2016·达州中考)如图，在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C，灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行，上午10：00在A处测得灯塔C位于轮船的北偏西30°方向，上午10：40在B处测得灯塔C位于轮船的北偏东60°方向，且与灯塔C相距12km. (1)若轮船照此速度与航向航向，何时到达海岸线？ (2)若轮船不改变航向，该轮船能否停靠在码头？请说明理由(参考数据：≈1.4，≈1.7)． 参考答案与解析 1．C　2.C　3.D　4.A　5.B　6.B 7．D　解析：根据圆周角定理，可得∠C＞∠D，根据锐角三角形函数的增减性，可得sinC＞sinD，故①正确；cosC＜cosD，故②错误；tanC＞tanD，故③正确． 8．D　解析：延长CB交PQ于点D.∵MN∥PQ，BC⊥MN，∴BC⊥PQ.∵自动扶梯AB的坡度为1∶2.4，∴＝＝.设BD＝5k米，AD＝12k米，则AB＝13k米．∵AB＝13米，∴k＝1，∴BD＝5米，AD＝12米．在Rt△CDA中，∠CDA＝90°，∠CAD＝42°，∴CD＝AD·tan∠CAD≈12×0.90＝10.8(米)，∴BC＝CD－BD≈10.8－5＝5.8(米)． 9．4　10.60°　11.　12.3　13.9 14．6　解析：综合三视图可知，这个几何体的底层有2＋1＋1＋1＝5个小正方体，第二层有1个小正方体，因此搭成这个几何体所用小正方体的个数是5＋1＝6个． 15．解：在Rt△ABD中，∵AD＝1，sinB＝，∴AB＝3，∴BD＝＝2.在Rt△ACD中，∵∠C＝45°，∴CD＝AD＝1.∴BC＝CD＋BD＝1＋2. 16．解：过点C作CD⊥AB于点D.设AD＝x米，小明的行走速度是a米/秒．∵∠A＝45°，CD⊥AB，∴AD＝CD＝x米，∴AC＝x(米)．在Rt△BCD中，∵∠B＝30°，∴BC＝＝2x(米)．∵小军的行走速度为米/秒，若小明与小军同时到达山顶C处，∴＝，解得a＝1. 答：小明的行走速度是1米/秒． 17．解：(1)如图所示； (2)由勾股定理得斜边长为10厘米，S底＝×8×6＝24(平方厘米)，S侧＝(8＋6＋10)×3＝72(平方厘米)，S全＝72＋24×2＝120(平方厘米)． 答：这个几何体的全面积是120平方厘米． 18．解：(1)延长AB交海岸线l于点D，过点B作BE⊥海岸线l于点E，过点A作AF⊥l于F，如图所示．∵∠BEC＝∠AFC＝90°，∠EBC＝60°，∠CAF＝30°，∴∠ECB＝30°，∠ACF＝60°，∴∠BCA＝90°.∵BC＝12km，AB＝36×＝24(km)，∴AB＝2BC，∴∠BAC＝30°，∠ABC＝60°.∵∠ABC＝∠BDC＋∠BCD＝60°，∴∠BDC＝∠BCD＝30°，∴BD＝BC＝12，∴所需时间t为＝(小时)＝20(分钟)，∴轮船照此速度与航向航行，上午11：00能到达海岸线； (2)∵BD＝BC，BE⊥CD，∴DE＝EC.在Rt△BEC中，∵BC＝12km，∠BCE＝30°，∴BE＝6km，EC＝6km，∴CD＝2EC＝12≈20.4(km)．∵20＜20.4＜21.5，∴不改变航向，轮船可以停靠在码头．