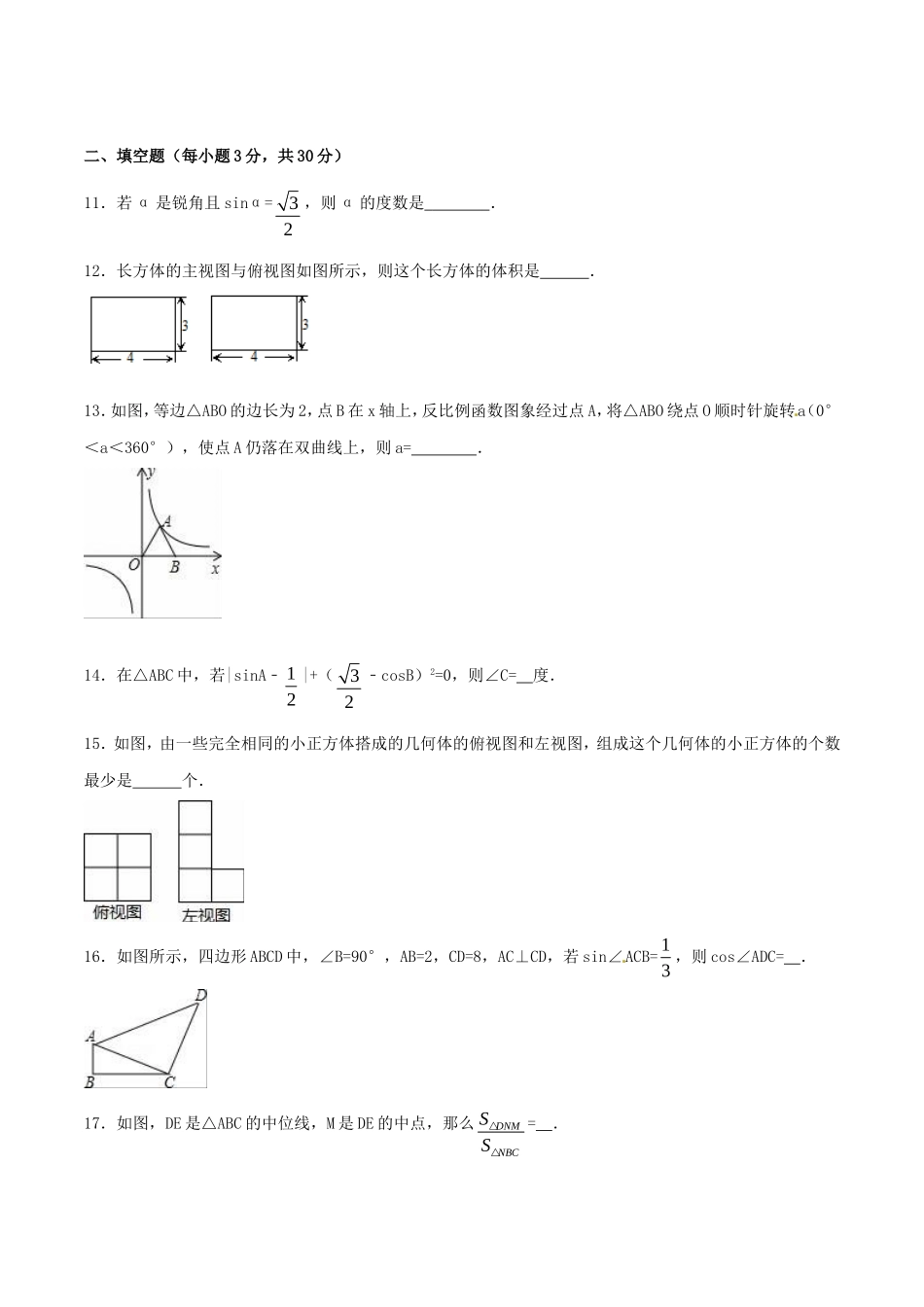
《九年下册期末》测试卷(A卷)(测试时间:120分钟满分:120分)一、选择题(每小题3分,共30分)1.当锐角A的cosA>22时,∠A的值为()A.小于45°B.小于30°C.大于45°D.大于30°2.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:体积x(mL)10080604020压强y(kPa)6075100150300则可以反映y与x之间的关系的式子是()A.y=3000xB.y=6000xC.y=D.y=3.已知线段a=3cm,b=12cm,若线段c是a,b的比例中项,则c的值为()A.2cmB.4cmC.6cmD.±6cm4.如图是一个由若干正方体组成的组合体的俯视图,数字表示所在位置正方体的个数,则这个组合体的侧视图是().A.B.C.D.5.如图,D,E分别为△ABC的边AB,AC的中点,则△ADE的面积与四边形BCED的面积比为()A.1∶2B.1∶3C.1∶4D.1∶16.坡度等于1:的斜坡的坡角等于()A.B.C.D.7.已知反比例函1yx的图像上有两点11,Axy、22,Bxy,且12xx,那么1y、2y的大小关系是().A.12yyB.12yyC.12yyD.不能确定8.如图所示,平地上一棵树高为6米,两次观察地面上的影子,第一次是当阳光与地面成60时,第二次是阳光与地面成30时,第二次观察到的影子比第一次长()A.633B.43C.63D.3239.如图是边长为1的六个小正方形组成的平面图形,经过折叠能围成一个正方体,那么点A,B在围成的正方体上相距()A.0B.1C.2D.310.如图所示,已知:(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2,此时P点的坐标为()A.(3,2)B.(,3)C.()D.(,)二、填空题(每小题3分,共30分)11.若α是锐角且sinα=32,则α的度数是.12.长方体的主视图与俯视图如图所示,则这个长方体的体积是.13.如图,等边△ABO的边长为2,点B在x轴上,反比例函数图象经过点A,将△ABO绕点O顺时针旋转a(0°<a<360°),使点A仍落在双曲线上,则a=.14.在△ABC中,若|sinA﹣12|+(32﹣cosB)2=0,则∠C=度.15.如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数最少是个.[来源:Zxxk.Com]16.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=13,则c...