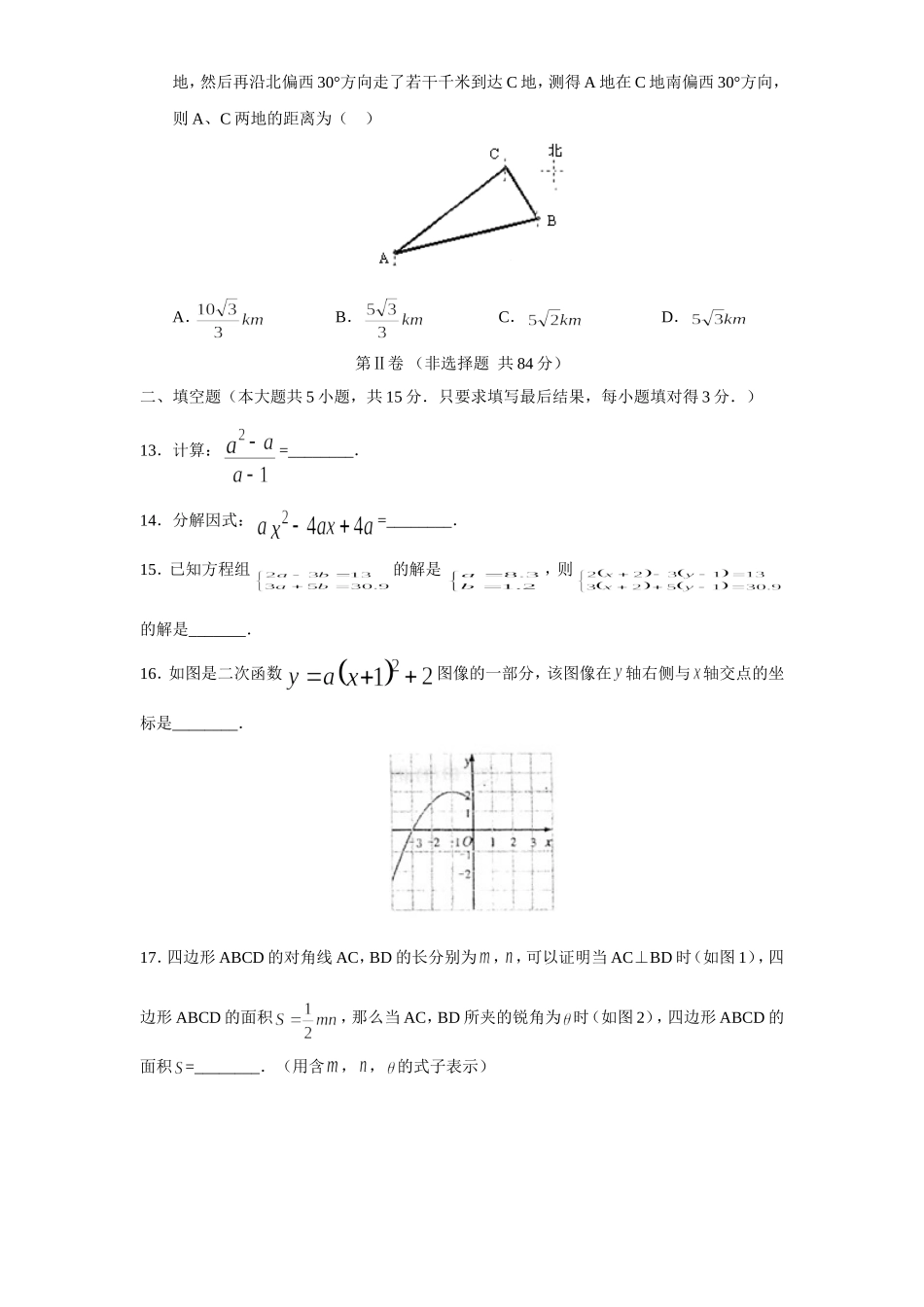
人教版九年级数学下册期中检测1附答案第Ⅰ卷选择题(共36分)一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记0分.)1.下列计算中正确的是()来源:www.bcjy123.com/tiku/A.B.C.D.2.通过世界各国卫生组织的协作和努力,甲型H1N1流感疫情得到了有效的控制,到目前为止,全球感染人数约为20000人左右,占全球人口的百分比约为0.0000031,将数字0.0000031用科学记数法表示为()A.B.C.D.3.若,则的平方根是()A.16B.±16C.2D.±24.关于的一元二次方程有一个根是0,则值为()A.1B.C.1或D.5.P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO等于().A.B.C.D.6.若,则不等式组的解集为()A.B.C.D.无解7.在拼图游戏中,从甲图的四张纸中,任取两张纸片拼成“小房子”(如乙图)的概率等于()A.1B.C.D.8.因为,所以,因为,所以,由此猜想、推理知:一般地当为锐角时有,由此可知:=()A.B.C.D.9.如图,直线与双曲线交于A、B两点,过点A作AM⊥轴,垂足为M,连结BM,若,则的值是()A.2B.C.D.410.如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为()米.A.B.1C.D.11.若为二次函数的图象上的三点,则的大小关系是()A.B.C.D.12.在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为()A.B.C.D.第Ⅱ卷(非选择题共84分)二、填空题(本大题共5小题,共15分.只要求填写最后结果,每小题填对得3分.)13.计算:=________.14.分解因式:=________.15.已知方程组的解是,则的解是_______.16.如图是二次函数图像的一部分,该图像在轴右侧与轴交点的坐标是________.17.四边形ABCD的对角线AC,BD的长分别为,,可以证明当AC⊥BD时(如图1),四边形ABCD的面积,那么当AC,BD所夹的锐角为时(如图2),四边形ABCD的面积=________.(用含,,的式子表示)三、解答题(本题共6小题,共69分.解答应写出文字说明、证明过程或推演步骤)18.(6分)一个布袋中有8个红球和16个白球,它们除颜色外都相同.(1)求从袋中摸出一个球是红球的概率;(2)现从袋中取走若干个白球,并放入相同数量的红球.搅...