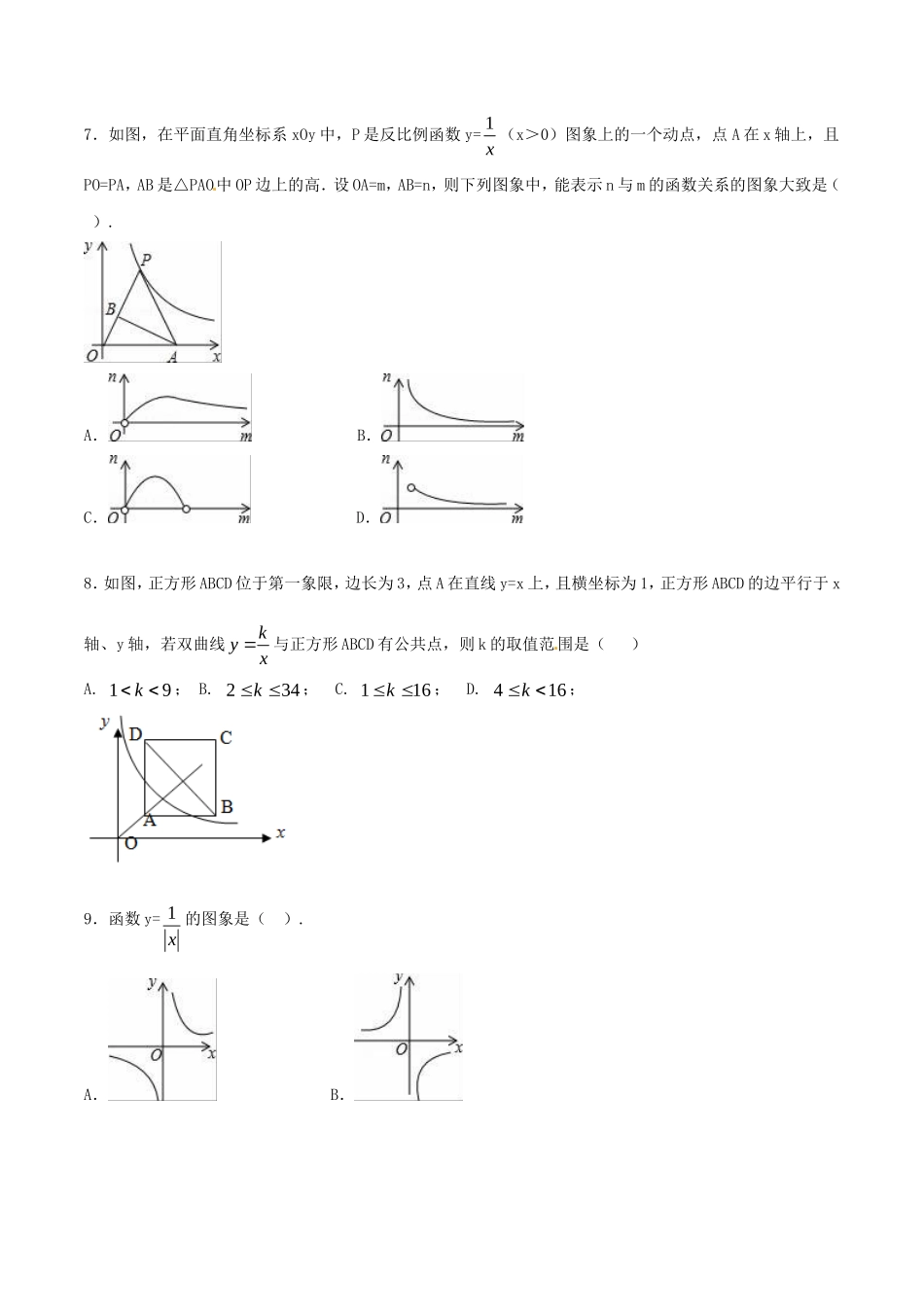
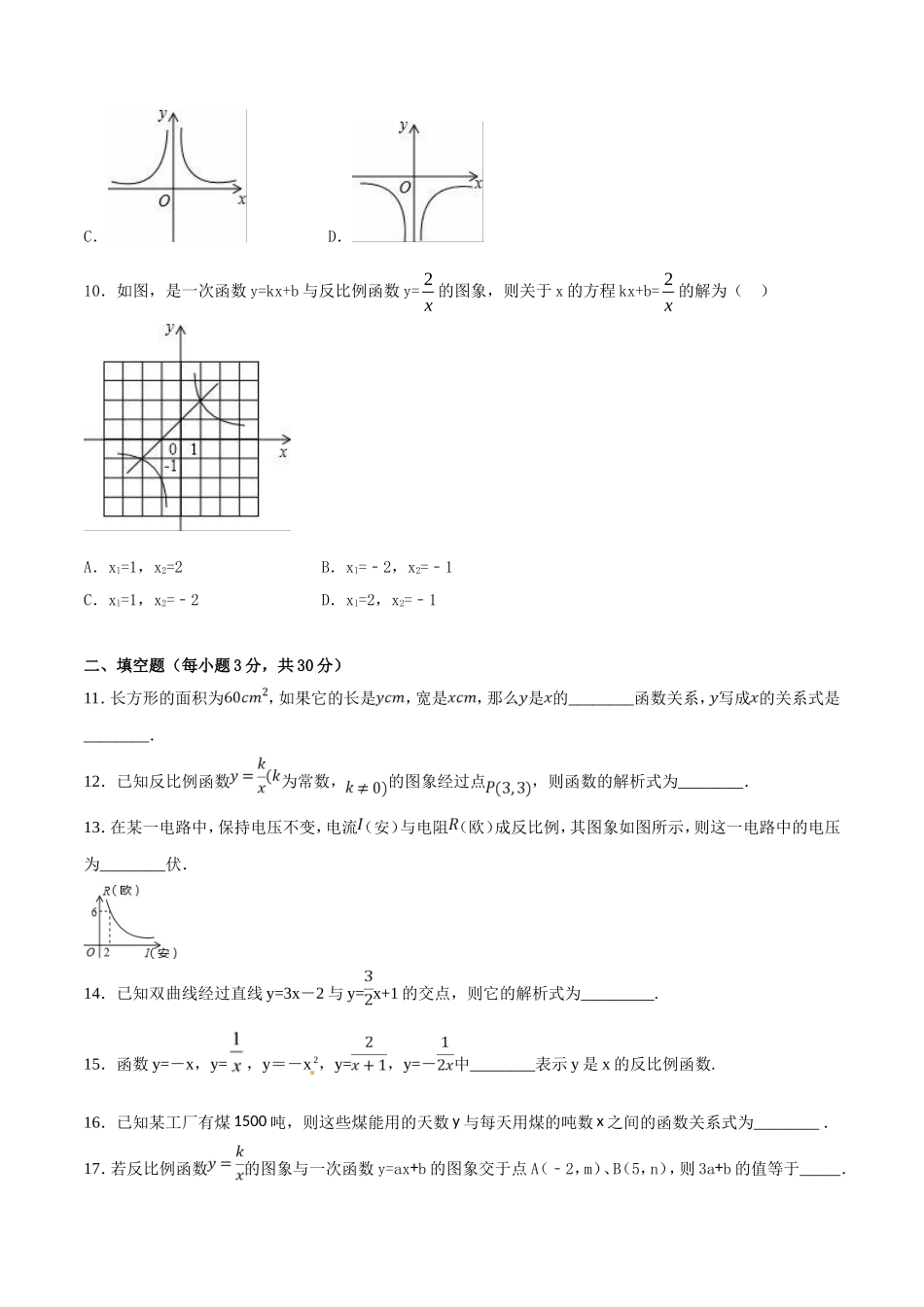
《第二十六章反比例函数》测试卷(B卷)(测试时间:120分钟满分:120分)[来源:学+科+网Z+X+X+K]一、选择题(每小题3分,共30分)1.反比例函数y=kx的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为().A.2B.﹣2C.4D.﹣42.反比例函数x2y的图象位于()A.第一、二象限B.第三、四象限C.第一、象限D.第二、四象限3.已知点(1,﹣2)在反比例函数kyx的图象上,那么这个函数图象一定经过点()A.(﹣1,2)B.(﹣2,﹣1)C.(﹣1,﹣2)D.(2,1)4.若点P(2,m)是反比例函数x4y图象上一点,则m的值是()A.1B.2C.3D.45.下列函数中,当x>0时,y随x的增大而减小的是()A.y=2xB.y=-4xC.y=3x+2D.y=x2-36.已知),(111yxP,),(222yxP,),(333yxP是反比例函数xy2的图象上的三点,且3210xxx,则321yyy、、的大小关系是()A.123yyyB.321yyyC.312yyyD.132yyy7.如图,在平面直角坐标系xOy中,P是反比例函数y=1x(x>0)图象上的一个动点,点A在x轴上,且PO=PA,AB是△PAO中OP边上的高.设OA=m,AB=n,则下列图象中,能表示n与m的函数关系的图象大致是().A.B.C.D.8.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,且横坐标为1,正方形ABCD的边平行于x轴、y轴,若双曲线kyx与正方形ABCD有公共点,则k的取值范围是()[来源:Z.xx.k.Com]A.19k;B.234k;C.116k;D.416k;9.函数y=1x的图象是().A.B.C.D.10.如图,是一次函数y=kx+b与反比例函数y=2x的图象,则关于x的方程kx+b=2x的解为()[来源:学§科§网]A.xl=1,x2=2B.xl=﹣2,x2=﹣1C.xl=1,x2=﹣2D.xl=2,x2=﹣1二、填空题(每小题3分,共30分)11.长方形的面积为,如果它的长是,宽是,那么是的________函数关系,写成的关系式是________.12.已知反比例函数为常数,的图象经过点,则函数的解析式为________.13.在某一电路中,保持电压不变,电流(安)与电阻(欧)成反比例,其图象如图所示,则这一电路中的电压为________伏.14.已知双曲线经过直线y=3x-2与y=x+1的交点,则它的解析式为_________.15.函数y=-x,y=,y=-x2,y=,y=-中________表示y是x的反比例函数.16.已知某工厂有煤1500吨,则这些煤能用的天数y与每天用煤的吨数x之间的函数关系式为________.17.若反比例函数的图象与一次函数y=ax+b的图象交于点A(﹣2,m)、B(5,n)...