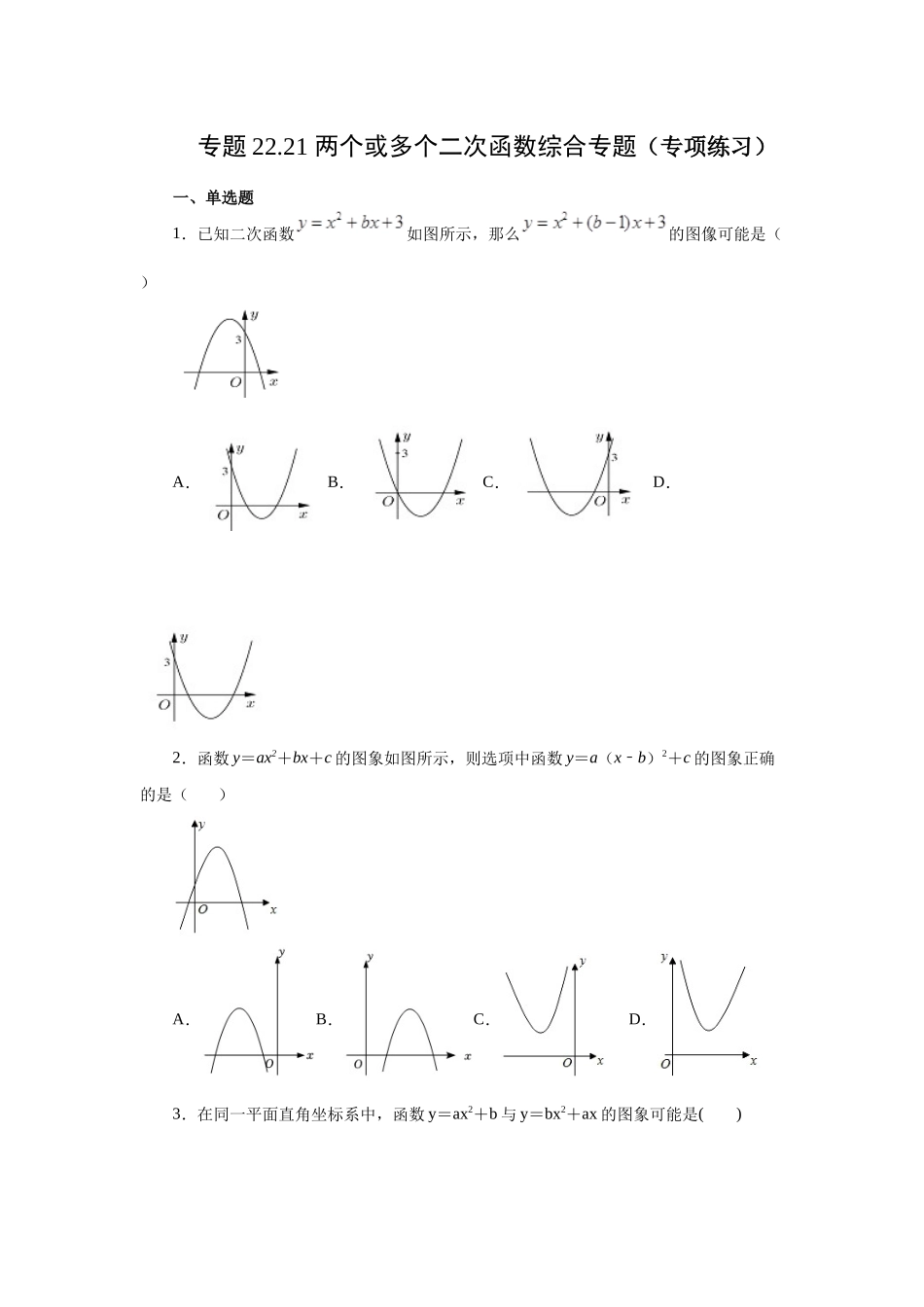
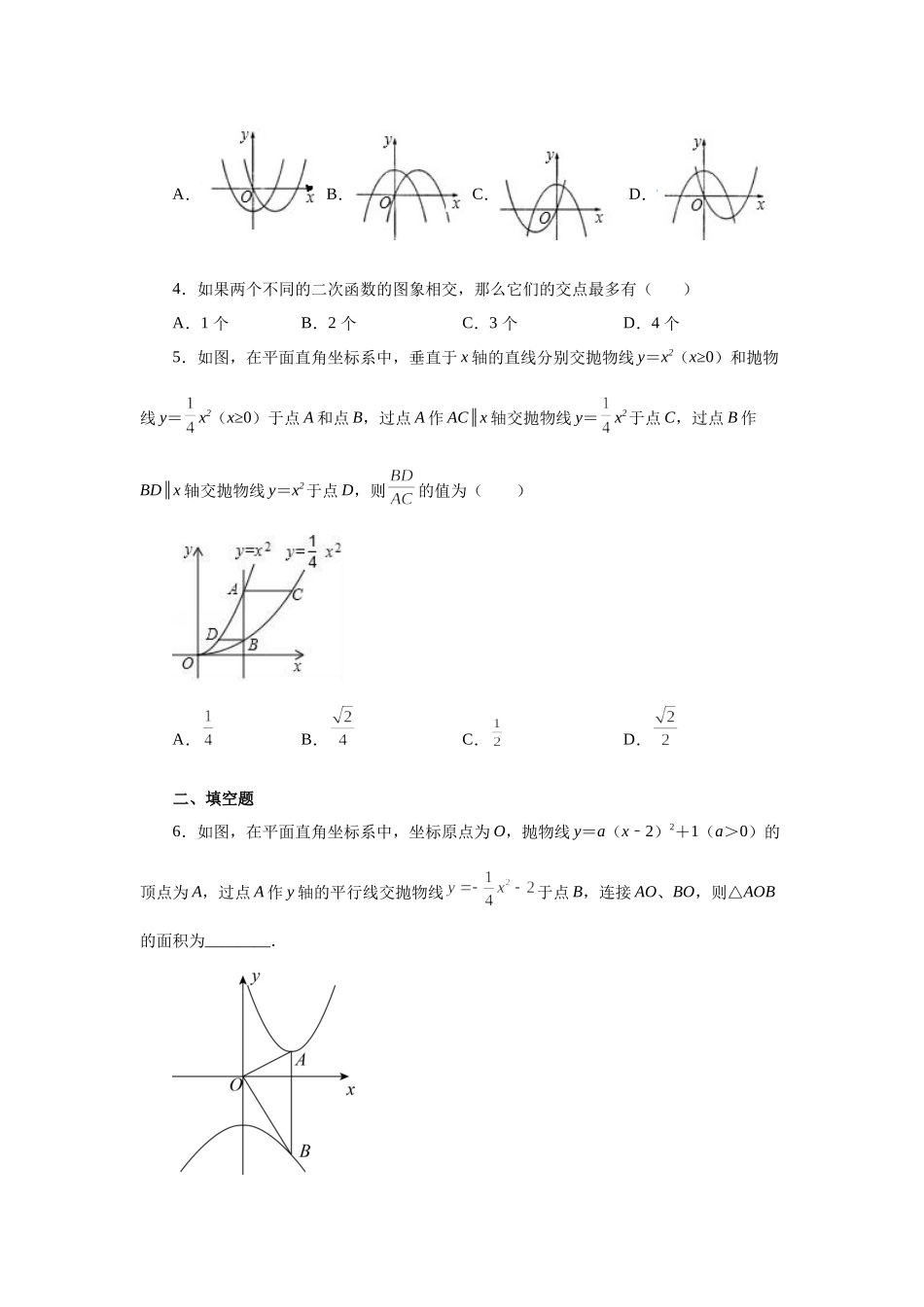
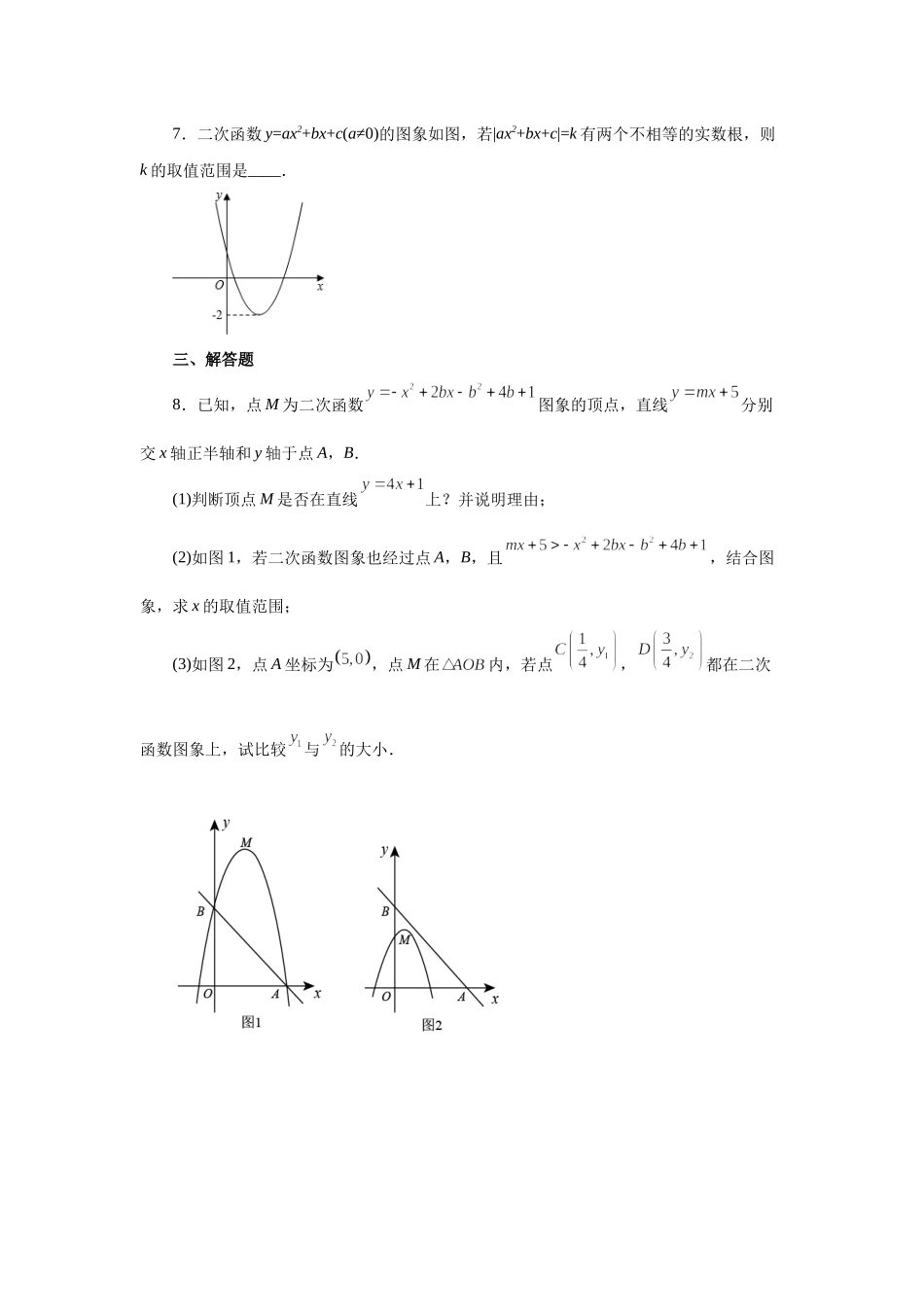
专题22.21两个或多个二次函数综合专题(专项练习)一、单选题1.已知二次函数如图所示,那么的图像可能是()A.B.C.D.2.函数y=ax2+bx+c的图象如图所示,则选项中函数y=a(x﹣b)2+c的图象正确的是()A.B.C.D.3.在同一平面直角坐标系中,函数y=ax2+b与y=bx2+ax的图象可能是()A.B.C.D.4.如果两个不同的二次函数的图象相交,那么它们的交点最多有()A.1个B.2个C.3个D.4个5.如图,在平面直角坐标系中,垂直于x轴的直线分别交抛物线y=x2(x≥0)和抛物线y=x2(x≥0)于点A和点B,过点A作AC∥x轴交抛物线y=x2于点C,过点B作BD∥x轴交抛物线y=x2于点D,则的值为()A.B.C.D.二、填空题6.如图,在平面直角坐标系中,坐标原点为O,抛物线y=a(x2﹣)2+1(a>0)的顶点为A,过点A作y轴的平行线交抛物线于点B,连接AO、BO,则△AOB的面积为________.7.二次函数y=ax2+bx+c(a≠0)的图象如图,若|ax2+bx+c|=k有两个不相等的实数根,则k的取值范围是____.三、解答题8.已知,点M为二次函数图象的顶点,直线分别交x轴正半轴和y轴于点A,B.(1)判断顶点M是否在直线上?并说明理由;(2)如图1,若二次函数图象也经过点A,B,且,结合图象,求x的取值范围;(3)如图2,点A坐标为,点M在内,若点,都在二次函数图象上,试比较与的大小.9.定义:若二次函数的图象记为,其顶点为,二次函数的图象记为,其顶点为,我们称这样的两个二次函数互为“反顶二次函数”.分类一:若二次函数经过的顶点B,且经过的顶点A,我们就称它们互为“反顶伴侣二次函数”.(1)所有二次函数都有“反顶伴侣二次函数”是______命题.(填“真”或“假”)(2)试求出的“反顶伴侣二次函数”.(3)若二次函数与互为“反顶伴侣二次函数”,试探究与的关系,并说明理由.(4)分类二:若二次函数可以绕点M旋转180°得到二次函数;,我们就称它们互为“反顶旋转二次函数”.①任意二次函数都有“反顶旋转二次函数”是______命题.(填“真”或“假”)②互为“反顶旋转二次函数”的对称中心点M有什么特点?③如图,,互为“反顶旋转二次函数”,点E,F的对称点分别是点Q,G,且轴,当四边形EFQG为矩形时,试探究二次函数,的顶点有什么关系.并说明理由.10.已知抛物线与轴交于点,其关于轴对称的抛物线为:,且经过点和点.(1)求抛物线的解析式;(2)将抛物线沿轴向右平移得到抛物线,抛物线与轴的交点记为点和点(在的右侧),与轴交于点,如果满足与...