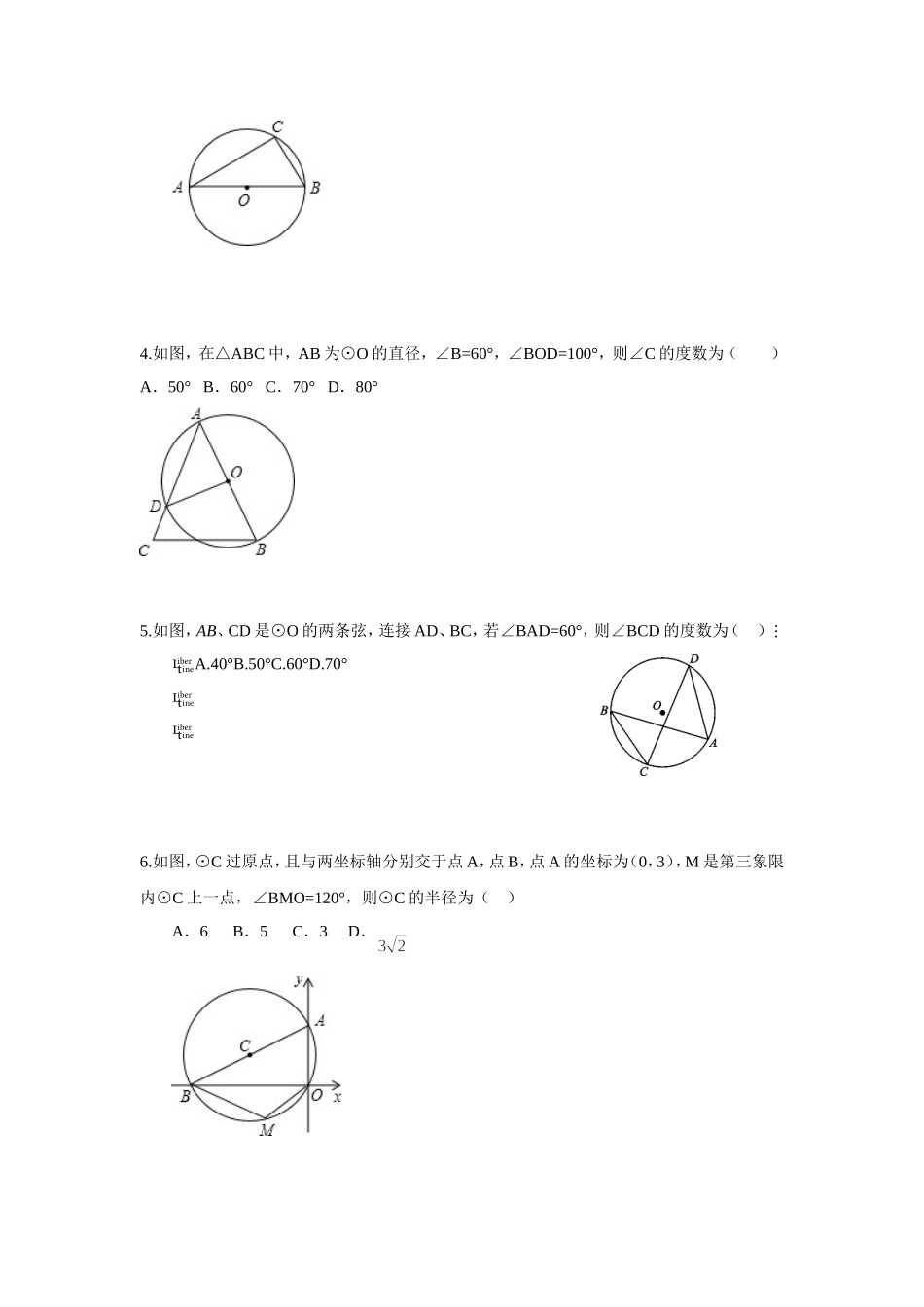
24.1圆(第四课时)--------圆周角知识点1、圆周角定义:顶点在,并且两边都和圆的角叫圆周角。2、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角,都等于这条弧所对的圆心角的。推论1、在同圆或等圆中,如果两个圆周角,那么它们所对的弧。推论2、半圆(或直径)所对的圆周角是;900的圆周角所对的弦是。3、圆内接四边形:定义:如果一个多边形的所有顶点都在圆上,这个多边形叫做,这个圆叫做。性质:圆内接四边形的对角一、选择题1.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有()A.1个B.2个C.3个D.4个2.如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为()A.20°B.40°C.60°D.80°3.如图,AB是⊙O的直径,点C在⊙O上,若∠A=40º,则∠B的度数为()A.80ºB.60ºC.50ºD.40ºC·BDOAACBO4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为()A.50°B.60°C.70°D.80°5.如图,AB、CD是⊙O的两条弦,连接AD、BC,若∠BAD=60°,则∠BCD的度数为()A.40°B.50°C.60°D.70°6.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为()A.6B.5C.3D.7、如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=23,则⊙O的半径为()A.43B.63C.8D.128、如图,DC是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()B.AF=BFC.OF=CFD.∠DBC=90°二、填空题1.如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是.2.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB=度.3.已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE=.4.如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD=..5、如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB=.6、如图,若AB是⊙O的直径,AB=10cm,∠CAB=30°,则BC=cm.7、如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为.8、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC=.ABCDO9、如图,圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD=.10、如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是度.三、解答题1、如图,⊙O的直径AB为...