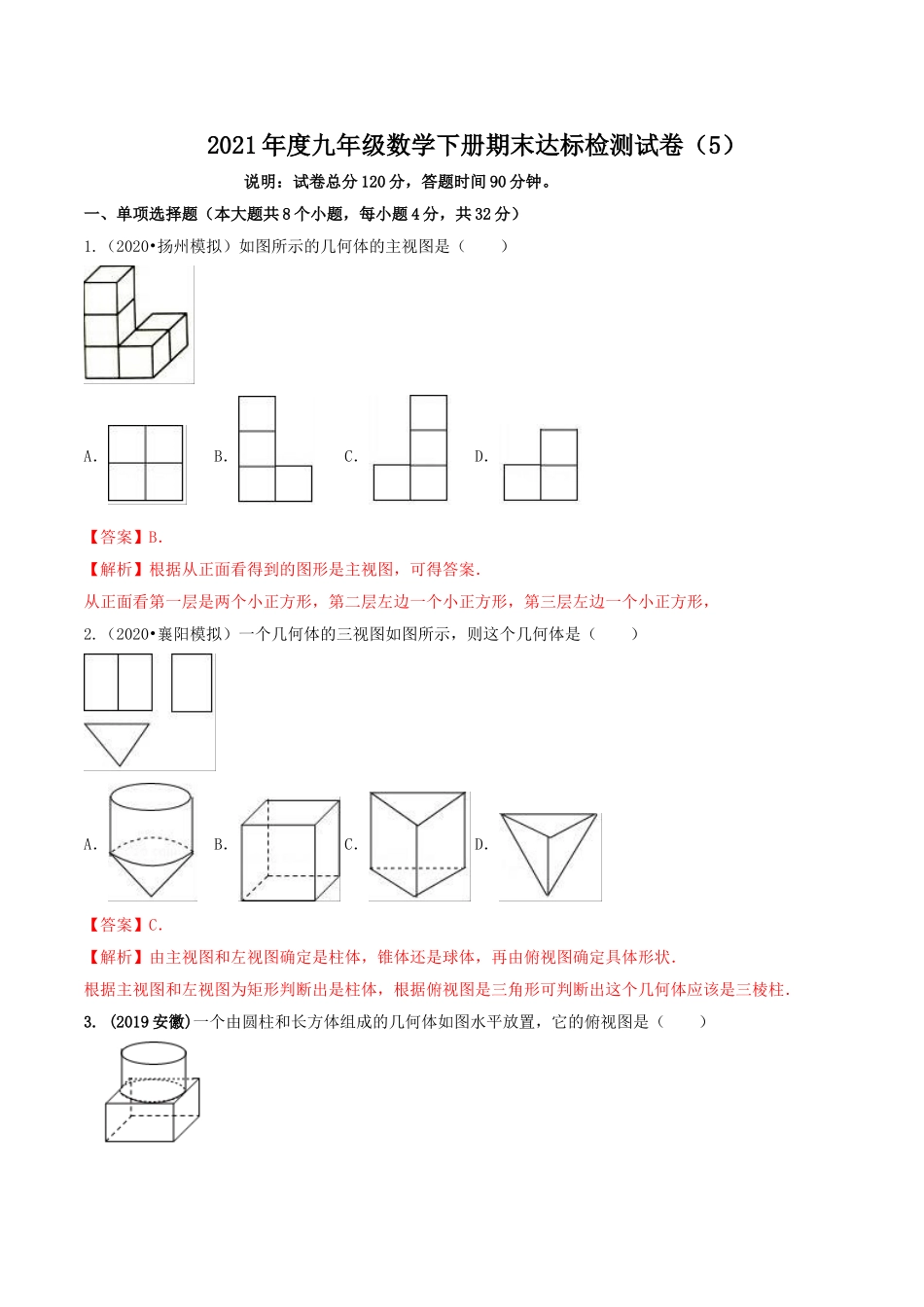
2021年度九年级数学下册期末达标检测试卷(5)说明:试卷总分120分,答题时间90分钟。一、单项选择题(本大题共8个小题,每小题4分,共32分)1.(2020•扬州模拟)如图所示的几何体的主视图是()A.B.C.D.【答案】B.【解析】根据从正面看得到的图形是主视图,可得答案.从正面看第一层是两个小正方形,第二层左边一个小正方形,第三层左边一个小正方形,2.(2020•襄阳模拟)一个几何体的三视图如图所示,则这个几何体是()A.B.C.D.【答案】C.【解析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.3.(2019安徽)一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是()A.B.C.D.【答案】C【解析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.几何体的俯视图是:4.(2019湖北仙桃)反比例函数y=-3/x,下列说法不正确的是()A.图象经过点(1,﹣3)B.图象位于第二、四象限C.图象关于直线y=x对称D.y随x的增大而增大【答案】D【解析】由点(1,﹣3)的坐标满足反比例函数y=-3/x,故A是正确的;由k=﹣3<0,双曲线位于二、四象限,故B也是正确的;由反比例函数的对称性,可知反比例函数y=-3/x关于y=x对称是正确的,故C也是正确的,由反比例函数的性质,k<0,在每个象限内,y随x的增大而增大,不在同一象限,不具有此性质,故D是不正确的。5.(2019黑龙江省龙东地区)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数的图象上,顶点B在反比例函数的图象上,点C在x轴的正半轴上,则平行四边形OABC的面积是()A.B.C.4D.6xyCBAO【答案】C【解析】反比例函数的图象和性质;平行四边形的面积。设A(a,b),B(a+m,b),依题意得,,∴,化简得m=4a. ,∴ab=1,∴S平行四边形OABC=mb=4ab=4×1=4,故选C.6.在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的面积之比为()A.B.C.D.【答案】C.【解析】由点D、E分别为边AB、AC的中点,可得出DE为△ABC的中位线,进而可得出DE∥BC及△ADE∽△ABC,再利用相似三角形的性质即可求出△ADE与△ABC的面积之比. 点D、E分别为边AB、AC的中点,∴DE为△ABC的中位线,∴DE∥BC,∴△ADE∽△ABC,∴=()2=.故选:C.7.(2019年广西玉林市)如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则是相似...