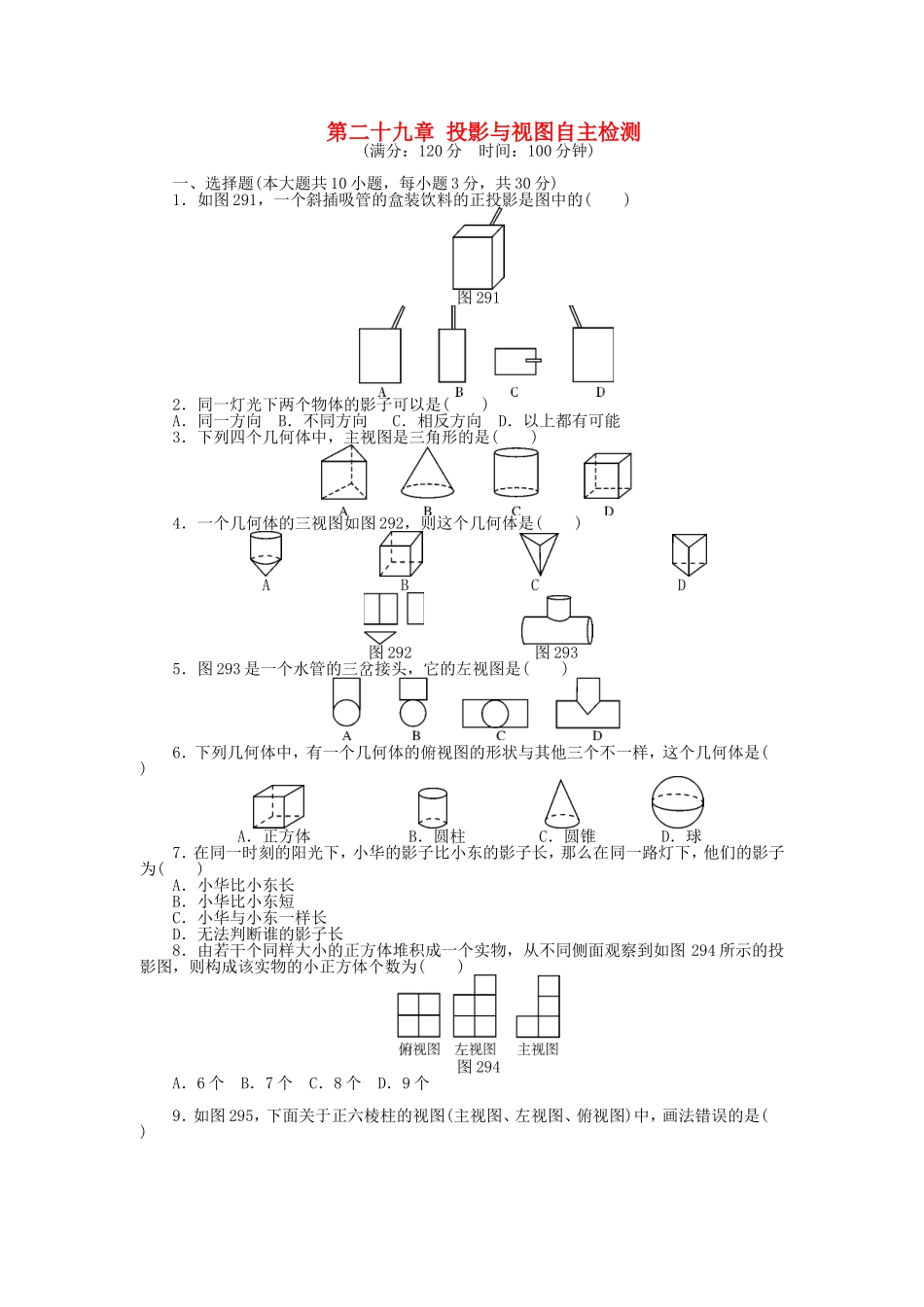
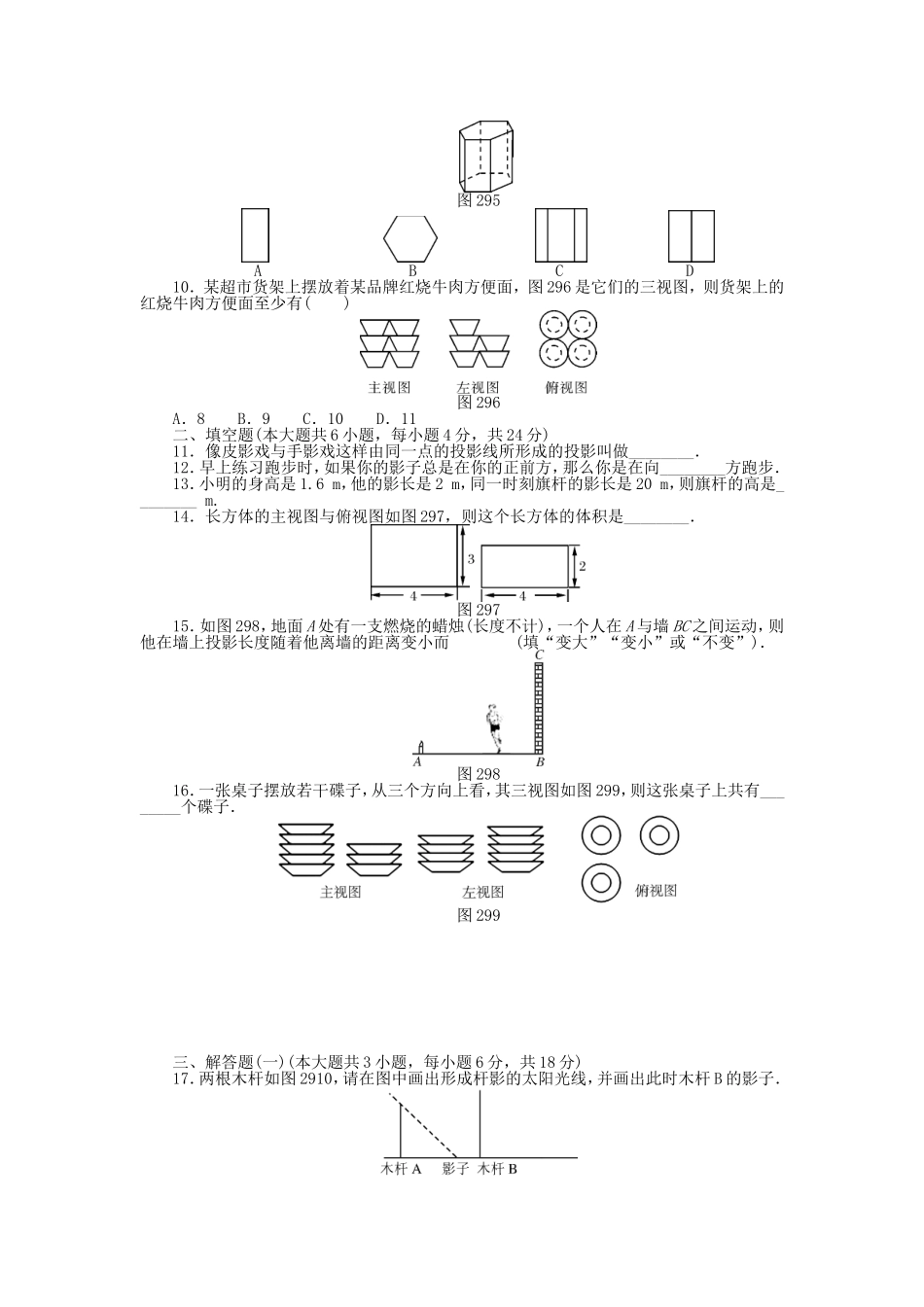
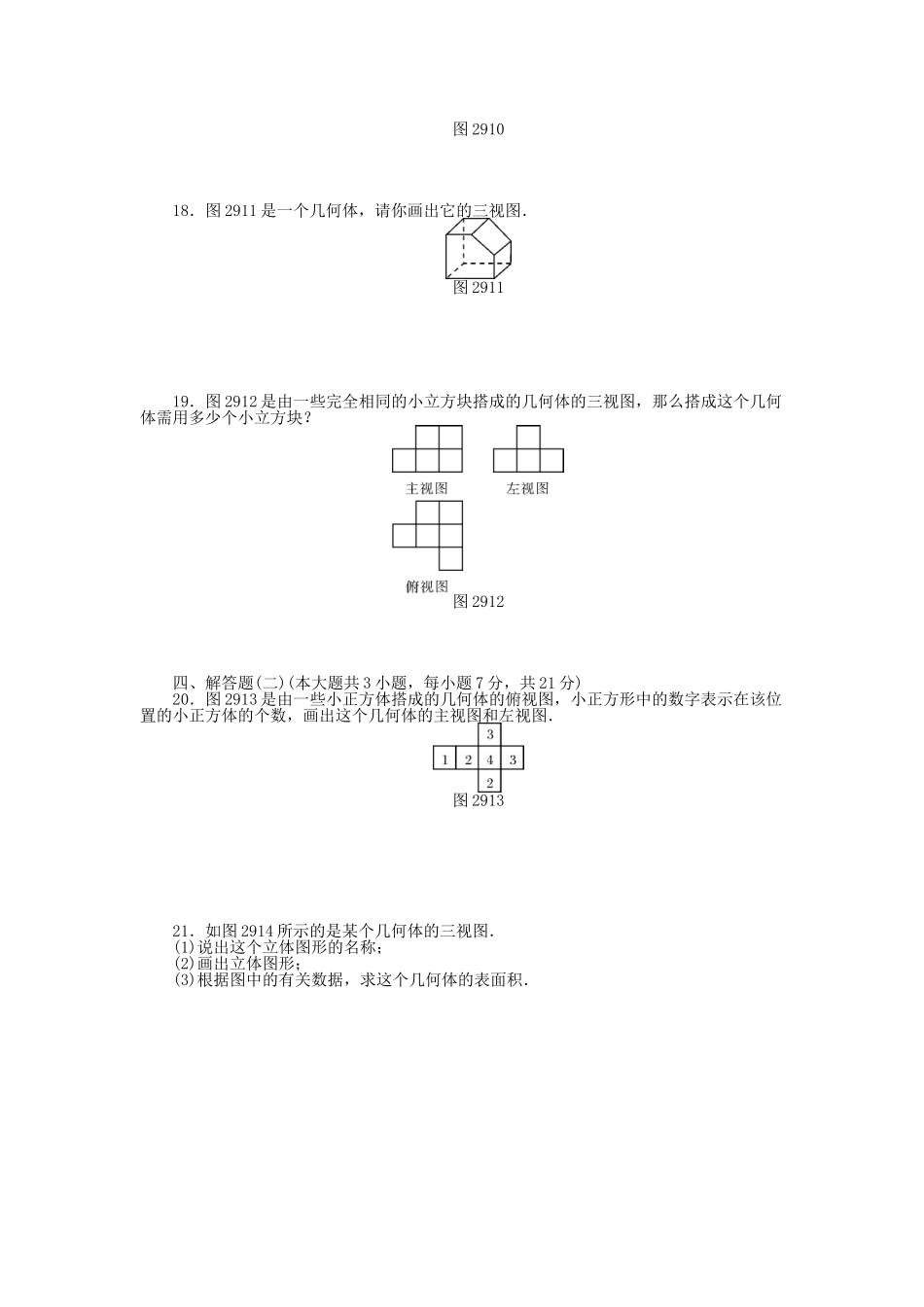
第二十九章投影与视图自主检测(满分:120分时间:100分钟)一、选择题(本大题共10小题,每小题3分,共30分)1.如图291,一个斜插吸管的盒装饮料的正投影是图中的()图2912.同一灯光下两个物体的影子可以是()A.同一方向B.不同方向C.相反方向D.以上都有可能3.下列四个几何体中,主视图是三角形的是()4.一个几何体的三视图如图292,则这个几何体是()ABCD图292图2935.图293是一个水管的三岔接头,它的左视图是()6.下列几何体中,有一个几何体的俯视图的形状与其他三个不一样,这个几何体是()A.正方体B.圆柱C.圆锥D.球7.在同一时刻的阳光下,小华的影子比小东的影子长,那么在同一路灯下,他们的影子为()A.小华比小东长B.小华比小东短C.小华与小东一样长D.无法判断谁的影子长8.由若干个同样大小的正方体堆积成一个实物,从不同侧面观察到如图294所示的投影图,则构成该实物的小正方体个数为()图294A.6个B.7个C.8个D.9个9.如图295,下面关于正六棱柱的视图(主视图、左视图、俯视图)中,画法错误的是()图295ABCD10.某超市货架上摆放着某品牌红烧牛肉方便面,图296是它们的三视图,则货架上的红烧牛肉方便面至少有()图296A.8B.9C.10D.11二、填空题(本大题共6小题,每小题4分,共24分)11.像皮影戏与手影戏这样由同一点的投影线所形成的投影叫做________.12.早上练习跑步时,如果你的影子总是在你的正前方,那么你是在向________方跑步.13.小明的身高是1.6m,他的影长是2m,同一时刻旗杆的影长是20m,则旗杆的高是________m.14.长方体的主视图与俯视图如图297,则这个长方体的体积是________.图29715.如图298,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上投影长度随着他离墙的距离变小而________(填“变大”“变小”或“不变”).图29816.一张桌子摆放若干碟子,从三个方向上看,其三视图如图299,则这张桌子上共有________个碟子.图299三、解答题(一)(本大题共3小题,每小题6分,共18分)17.两根木杆如图2910,请在图中画出形成杆影的太阳光线,并画出此时木杆B的影子.图291018.图2911是一个几何体,请你画出它的三视图.图291119.图2912是由一些完全相同的小立方块搭成的几何体的三视图,那么搭成这个几何体需用多少个小立方块?图2912四、解答题(二)(本大题共3小题,每小题7分,共21分)20.图2913是由一些小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的...