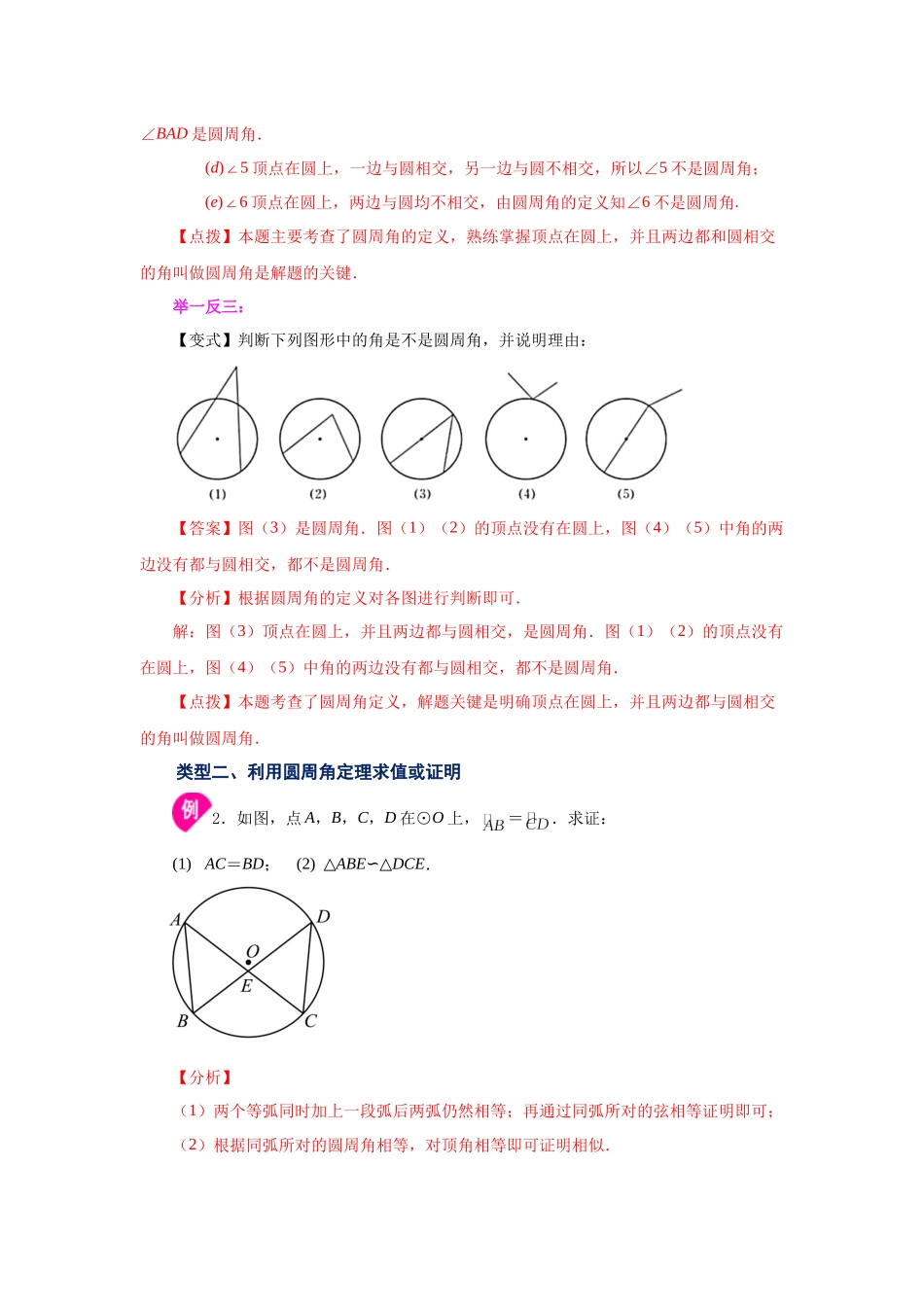
专题24.10圆周角(知识讲解)【学习目标】1.了解并圆周角的概念,识别圆周角;2.理解圆周角定理及其推论,能灵活运用圆周角的定理及其推理解决有关问题;【要点梳理】【知识点一】定义:顶点在圆上,角的两边都与圆相交的角。(两条件缺一不可);【知识点二】圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。【知识点三】圆周角定理推论:推论1:在同圆或等圆中,相等的圆周角所对的弧相等;推论2:直径(半圆)所对的圆周角是直角;90度的圆周角所对的弦为直径。【知识点四】常见的辅助线作法:①常见辅助线:有直径可构成直角,有90度圆周角可构成直径;②找圆心的方法:作两个90度圆周角所对两弦交点)。【知识点五】圆内接四边形性质:1、圆内接四边形的性质定理:圆内接四边形的对角互补。(任意一个外角等于它的内对角)【知识点六】补充知识点:补充1:两条平行弦所夹的弧相等;补充2:圆的两条弦1在圆外相交时,所夹角等于它所对的两条弧度数差的一半;(2)在圆内相交时,所夹的角等于它所夹两条弧度数和的一半;补充3:同弧所对的(在弧的同侧)圆内部角最大其次是圆周角,最小的是圆外角。【典型例题】类型一、圆周角概念1.观察下图中角的顶点与两边有何特征?指出哪些角是圆周角?【答案】特征见分析,(c)图中∠3、∠4、∠BAD是圆周角解:(a)1∠顶点在⊙O内,两边与圆相交,所以∠1不是圆周角;(b)2∠顶点在圆外,两边与圆相交,所以∠2不是圆周角;(c)图中∠3、∠4、∠BAD的顶点在圆周上,两边均与圆相交,所以∠3、∠4、∠BAD是圆周角.(d)5∠顶点在圆上,一边与圆相交,另一边与圆不相交,所以∠5不是圆周角;(e)6∠顶点在圆上,两边与圆均不相交,由圆周角的定义知∠6不是圆周角.【点拨】本题主要考查了圆周角的定义,熟练掌握顶点在圆上,并且两边都和圆相交的角叫做圆周角是解题的关键.举一反三:【变式】判断下列图形中的角是不是圆周角,并说明理由:【答案】图(3)是圆周角.图(1)(2)的顶点没有在圆上,图(4)(5)中角的两边没有都与圆相交,都不是圆周角.【分析】根据圆周角的定义对各图进行判断即可.解:图(3)顶点在圆上,并且两边都与圆相交,是圆周角.图(1)(2)的顶点没有在圆上,图(4)(5)中角的两边没有都与圆相交,都不是圆周角.【点拨】本题考查了圆周角定义,解题关键是明确顶点在圆上,并且两边都与圆相交的角叫做圆周角.类型二、利用圆周角定理求值或证明2.如图,...