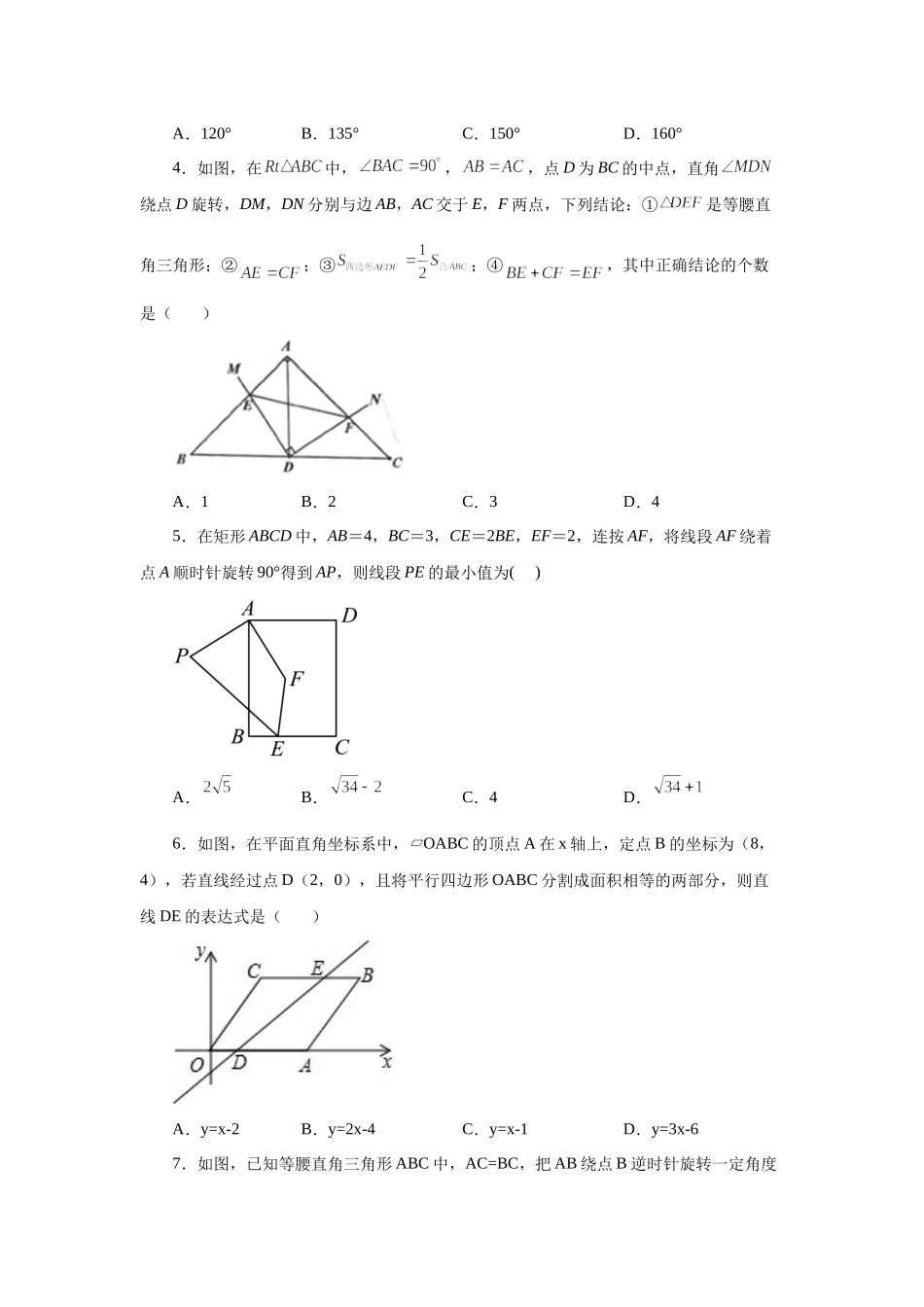
专题23.10《旋转》全章复习与巩固(培优篇)(专项练习)一、单选题1.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形.若点A的坐标是(1,3),则点M和点N的坐标分别是()A.M(1,﹣3),N(﹣1,﹣3)B.M(﹣1,﹣3),N(﹣1,3)C.M(﹣1,﹣3),N(1,﹣3)D.M(﹣1,3),N(1,﹣3)2.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则的值为()A.B.C.D.3.如图,是正三角形内的一点,且,,.若将绕点逆时针旋转后,得到,则等于().A.120°B.135°C.150°D.160°4.如图,在中,,,点D为BC的中点,直角绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①是等腰直角三角形;②;③;④,其中正确结论的个数是()A.1B.2C.3D.45.在矩形ABCD中,AB=4,BC=3,CE=2BE,EF=2,连按AF,将线段AF绕着点A顺时针旋转90°得到AP,则线段PE的最小值为()A.B.C.4D.6.如图,在平面直角坐标系中,OABC的顶点A在x轴上,定点B的坐标为(8,4),若直线经过点D(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线DE的表达式是()A.y=x-2B.y=2x-4C.y=x-1D.y=3x-67.如图,已知等腰直角三角形ABC中,AC=BC,把AB绕点B逆时针旋转一定角度到点D,连接AD、DC,使得∠DAC=BDC∠,当DC=时,线段AC的长()A.3B.C.D.8.对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是()A.12B.14C.16D.189.在平面直角坐标系中,抛物线与轴交于点,则该抛物线关于点成中心对称的抛物线的表达式为()A.B.C.D.10.如图,在平面直角坐标系中,点,,的坐标分别为,,.一个电动玩具从原点出发,第一次跳跃到点,使得点与点关于点成中心对称;第二次跳跃到点,使得点与点关于点成中心对称;第三次跳跃到点,使得点与点关于点成中心对称;第四次跳跃到点,使得点与点关于点成中心对称;….电动玩具照此规律跳下去,则点的坐标是().A.B.C.D.二、填空题11.如图,已知△ABC中,∠C=90°,AC=BC,将△ABC绕点A逆时针反向旋转60°到△AB′C′的位置,连...