【人教版】九年级上期末数学试卷6.doc

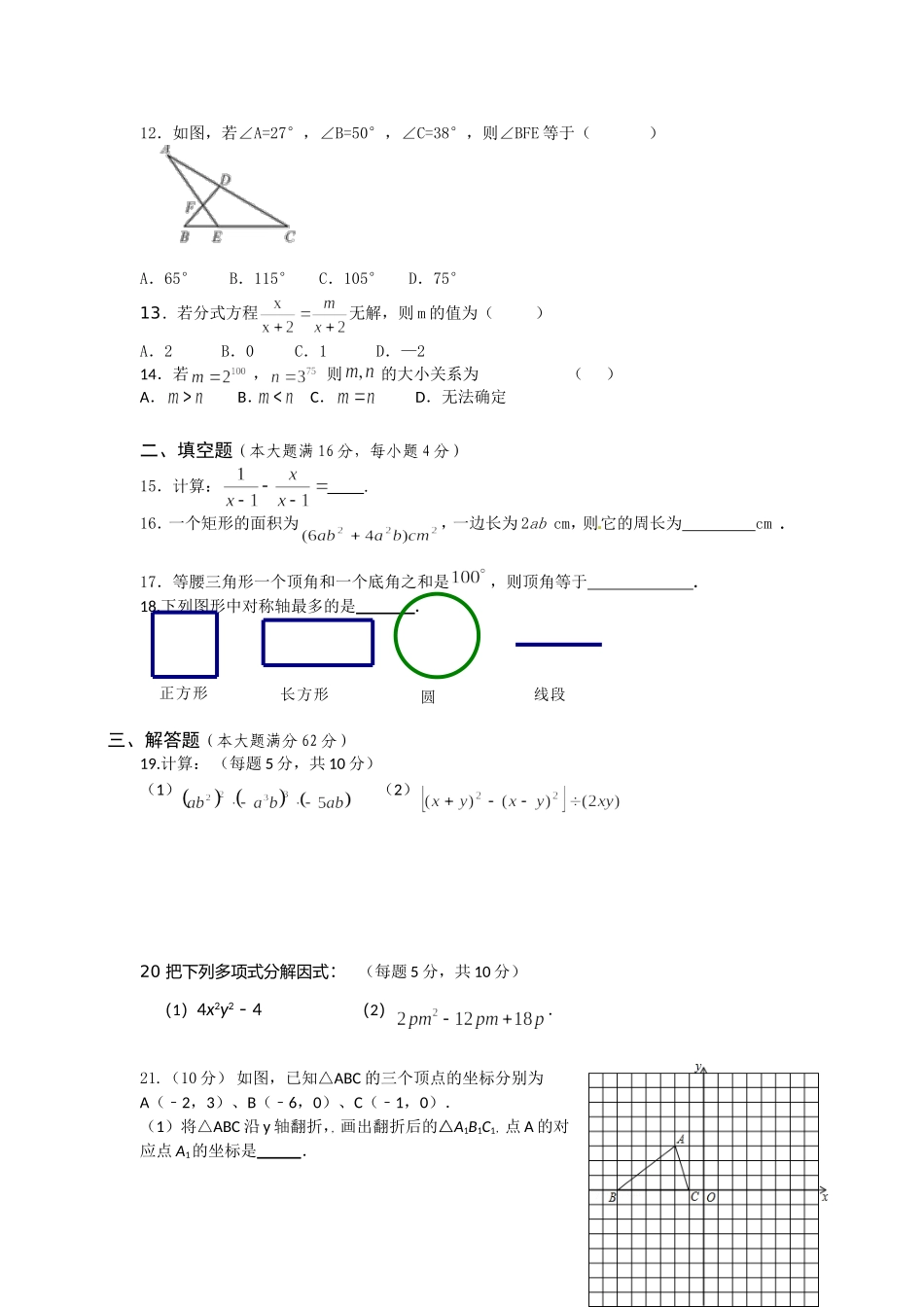
第一学期九年级期末考试数学试题 一、选择题 （每小题3分，共42分） 1．计算a7•（）2的结果是（ ） A．a B．a5 C．a6 D．a8 2．要使分式有意义，则x的取值范围是（ ） A、x≠1 B、x＞1 C、x＜1 D、x≠ 3．下列手机屏幕解锁图案中不是轴对称图形的是（ ） A． B． C． D． 4.根据下列已知条件，能唯一画出△ABC的是( ) A．AB=2，BC=4，AC=7 B．AB=5，BC=3，∠A=30° C．∠A=60°，∠B=45°，AC=4 D．∠C=90°，AB=6 5．下列各式，，，，中，是分式的共有（ ） A.1个 B.2个 C.3个 D.4个 6．若（x+3）（x-4）=x2+px+q，那么p、q的值是（ ） A．p=1，q=－12 B．p=－1，q=－12 C．p=7，q=12 D．p=7，q=－12 7．下列能判定△ABC为等腰三角形的是（ ） A．AB=AC=3，BC=6 B．∠A=40º、∠B=70º C．AB=3、BC=8，周长为16 D．∠A=40º、∠B=50º 8．若一个多边形的每一个外角都是45°，则这个多边形是（ ） A．六边形 B．八边形 C．九边形 D．十边形 9．如图，AB∥CD， BC∥AD，AB=CD，BE=DF，图中全等的三角形的对数是 A．1 B.2 C.3 D.4 10．如图，直线a∥b，点B在直线b上，且AB⊥BC，∠2=55°，则∠1的度数为（ ） A．65° B．25° C．35° D．45° 11．已知是完全平方式，则m的值是 （ ） A． B．25 C．5 D． 12．如图，若∠A=27°，∠B=50°，∠C=38°，则∠BFE等于（ ） A．65° B．115° C．105° D．75° 13．若分式方程无解，则m的值为（ ） A．2 B．0 C．1 D．—2 14．若 ， 则 的大小关系为 （ ） A． B． C． D．无法确定 二、填空题（本大题满16分，每小题4分） 15．计算： . 16．一个矩形的面积为，一边长为2ab cm，则它的周长为 cm . 17．等腰三角形一个顶角和一个底角之和是，则顶角等于 . 18.下列图形中对称轴最多的是 . 三、解答题（本大题满分62分） 19.计算： （每题5分，共10分） （1） （2） 20 把下列多项式分解因式： （每题5分，共10分） （1）4x2y2－4 （2）． 21.（10分） 如图，已知△ABC的三个顶点的坐标分别为 A（﹣2，3）、B（﹣6，0）、C（﹣1，0）． （1）将△ABC沿y轴翻折，，画出翻折后的△A1B1C1，点A的对应点A1的坐标是 ． (2) △ABC关于x轴对称的图形△A2B2C2， 直接写出点A2的坐标 ． （3）若△DBC与△ABC全等（点D与点A重合除外），请直接写出满足条件点D的坐标． 22.（10分）如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE． 求证：（1）△AEF≌△CEB； （2）AF=2CD． [来源:学+科+网Z+X+X+K] 23 （10分）．有两块面积相同的试验田，分别收获蔬菜900kg和1500kg，已知第一块试验田每亩收获蔬菜比第二块少300kg，求第一块试验田每亩收获蔬菜多少千克？ 24．（12分）（1）如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得线段BE、EF、FD之间的数量关系为 ． （2）如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF=∠BAD，线段BE、EF、FD之间存在什么数量关系，为什么？ （3）如图3，点A在点O的北偏西30°处，点B在点O的南偏东70°处，且AO=BO，点A沿正东方向移动249米到达E处，点B沿北偏东50°方向移动334米到达点F处，从点O观测到E、F之间的夹角为70°，则根据（2）的结论E、F之间的距离是多少？并说明理由． 选择题 BADCC BDBCC AADB 15 -1 16 3b+2a 17 20° 18 圆 19、计算：（每题5分，共10分） （1）解：原式=（3分） = （3分） （2）解：原式= （3分） =2 （3分） 20 （1） 4（xy+1）（xy-1） （2） 21、 （1）∵AD⊥BC，CE⊥AB ∴∠AEF=∠CEB=90° 即∠AFE+∠EAF=∠CFD+∠ECB=90° 又∵∠AEF=∠CFD ∴∠EAF=∠ECB 在△AEF和△CEB中，∠AEF=∠CEB，AE=CE，∠EAF=∠ECB ∴△AEF≌△CEB （6分） （2） 由△AEF≌△CEB得：AF=BC 在△ABC中，AB=AC，AD⊥BC ∴CD=BD，BC=2CD ∴AF=2CD. （4分） 22 （1） 画图 3分 A1（2,3） （2分） （2） （-2，-3） （2分） （3） （-5,3） （-5，-3） （-2，-3） （3分） 23 解：设第一块试验田每亩收获蔬菜x千克，由题意得：（1分） ， （4分） 解得：x=450， （2分） 经检验：x=450是原分式方程的解， （2分） 答：第一块试验田每亩收获蔬菜450千克． （1分） 24 （1）EF=BE+DF；（2分） （2）EF=BE+DF仍然成立．（1分） 证明：如图2，延长FD到G，使DG=BE，连接AG， ∵∠B+∠ADC=180°，∠ADC+∠ADG=180°， ∴∠B=∠ADG，在△ABE和△ADG中， ， ∴△ABE≌△ADG（SAS）， （2分） ∴AE=AG，∠BAE=∠DAG， ∵∠EAF=∠BAD， ∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF， ∴∠EAF=∠GAF， 在△AEF和△GAF中， ， ∴△AEF≌△GAF（SAS）， （2分） ∴EF=FG， ∵FG=DG+DF=BE+DF， ∴EF=BE+DF； （1分） （3）E、F之间的距离是583米。 （1分） 如图3，连接EF，延长AE、BF相交于点C， ∵∠AOB=（90°﹣70°）°+90°+（90°﹣60°）=140°，∠EOF=70°， ∴∠EOF=∠AOB， 又∵OA=OB， ∠OAC+∠OBC=（90°﹣20°+50°）+60°=180°， ∴符合探索延伸中的条件， ∴结论EF=AE+BF成立， 即EF=583米． （3分）