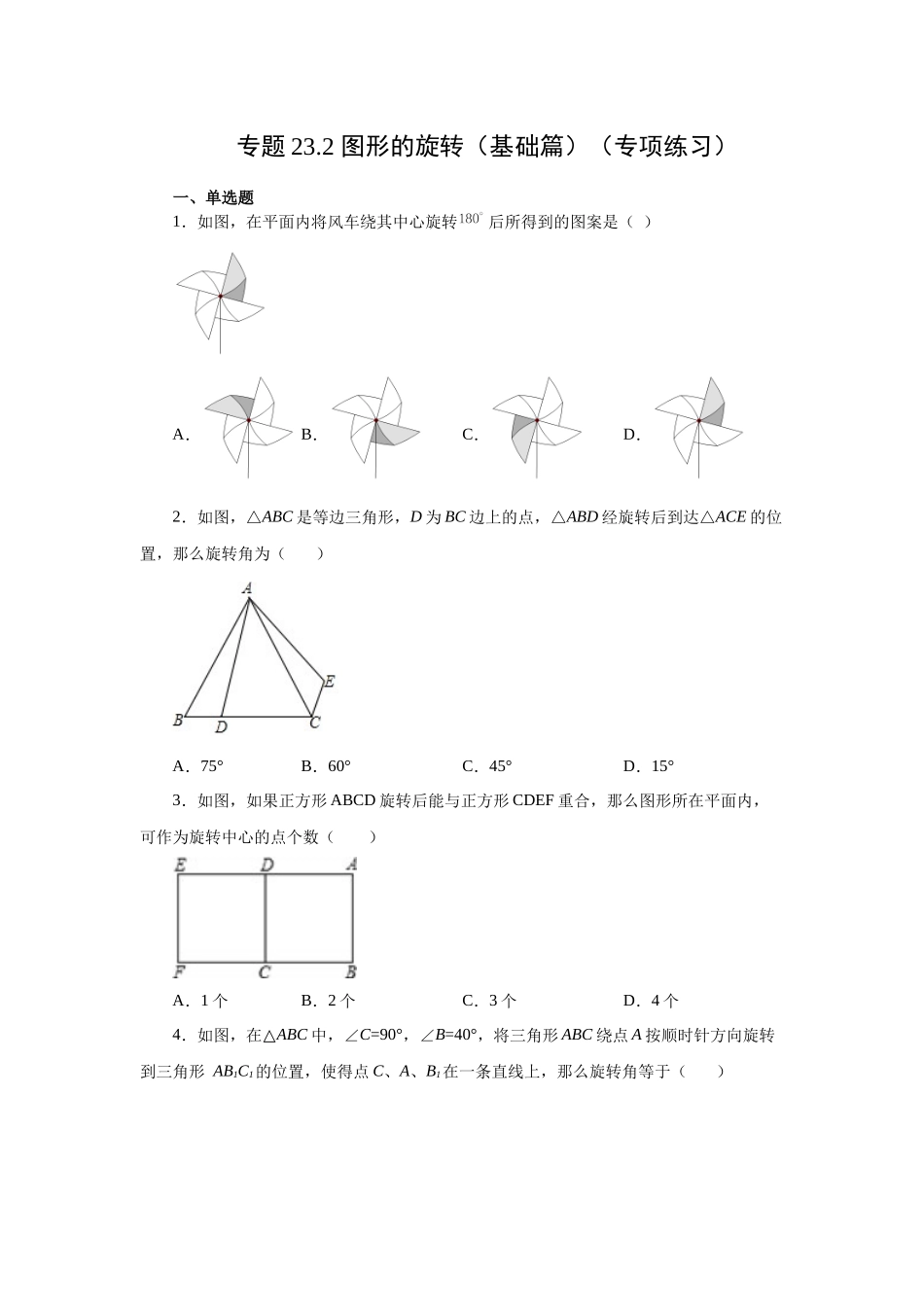
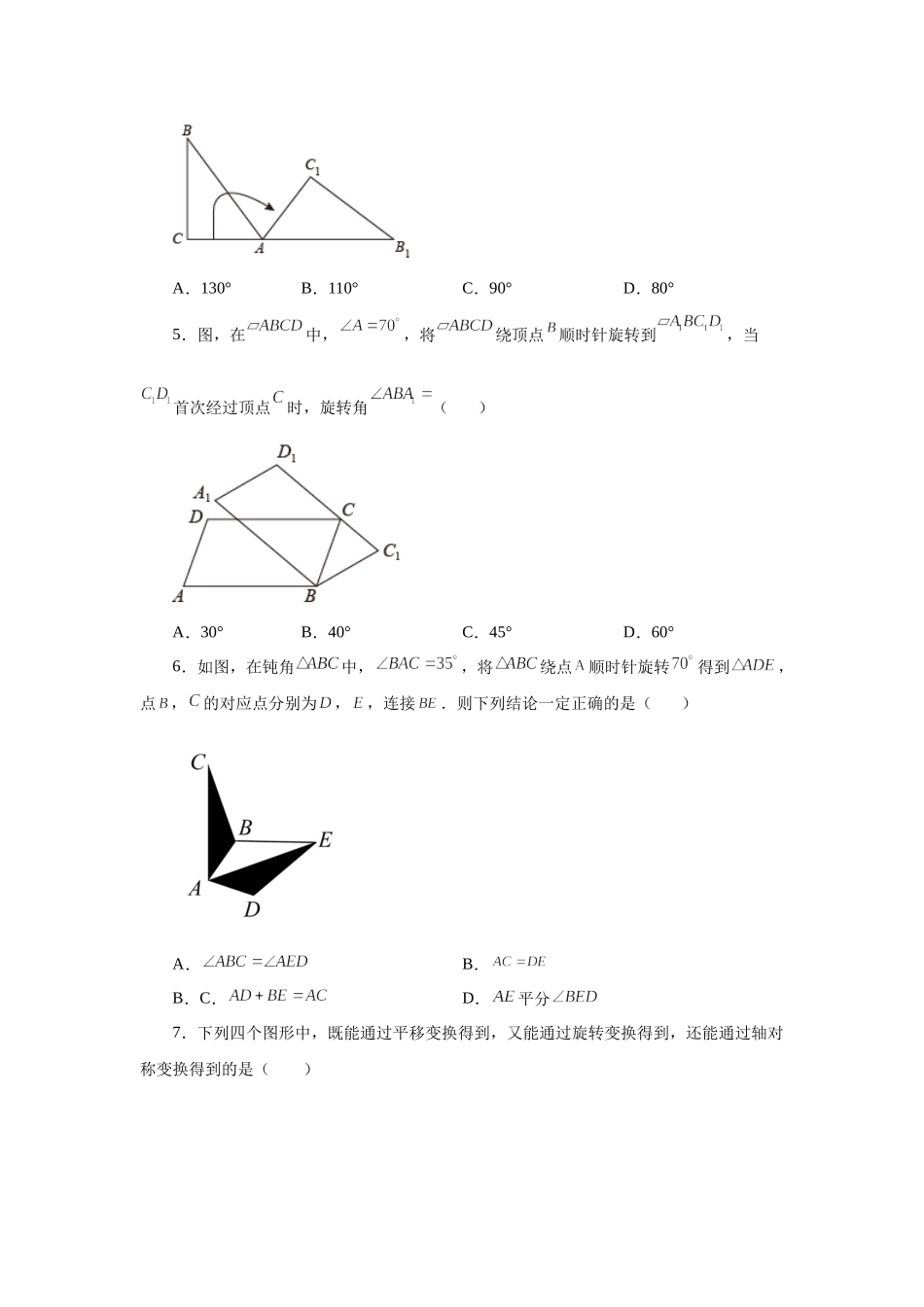
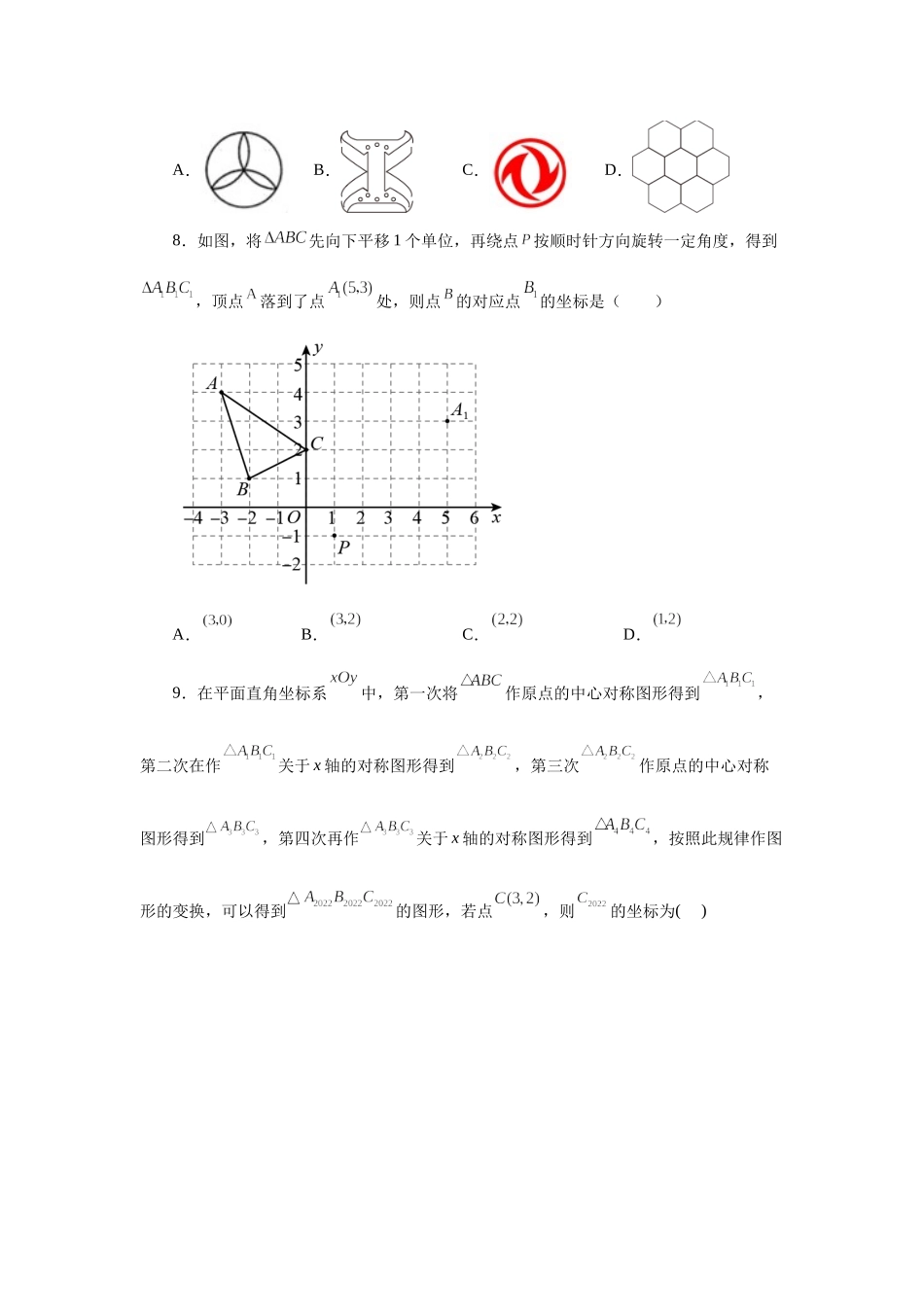
专题23.2图形的旋转(基础篇)(专项练习)一、单选题1.如图,在平面内将风车绕其中心旋转后所得到的图案是()A.B.C.D.2.如图,△ABC是等边三角形,D为BC边上的点,△ABD经旋转后到达△ACE的位置,那么旋转角为()A.75°B.60°C.45°D.15°3.如图,如果正方形ABCD旋转后能与正方形CDEF重合,那么图形所在平面内,可作为旋转中心的点个数()A.1个B.2个C.3个D.4个4.如图,在△ABC中,∠C=90°,∠B=40°,将三角形ABC绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在一条直线上,那么旋转角等于()A.130°B.110°C.90°D.80°5.图,在中,,将绕顶点顺时针旋转到,当首次经过顶点时,旋转角()A.30°B.40°C.45°D.60°6.如图,在钝角中,,将绕点顺时针旋转得到,点,的对应点分别为,,连接.则下列结论一定正确的是()A.B.B.C.D.平分7.下列四个图形中,既能通过平移变换得到,又能通过旋转变换得到,还能通过轴对称变换得到的是()A.B.C.D.8.如图,将先向下平移1个单位,再绕点按顺时针方向旋转一定角度,得到,顶点落到了点处,则点的对应点的坐标是()A.B.C.D.9.在平面直角坐标系中,第一次将作原点的中心对称图形得到,第二次在作关于x轴的对称图形得到,第三次作原点的中心对称图形得到,第四次再作关于x轴的对称图形得到,按照此规律作图形的变换,可以得到的图形,若点,则的坐标为()A.B.C.D.10.将抛物线绕坐标原点O旋转180°,所得抛物线的解析式为()A.B.C.D.11.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形,则它们的公共部分的面积等于()A.1﹣B.1﹣C.D.二、填空题12.正六边形可以看成由基本图形________经过________次旋转而成.13.如图,已知点A(3,0),B(1,4),C(3,﹣2),D(7,0),连接AB,CD,将线段AB绕着某一点旋转一定角度,使A,B分别与C,D重合,则旋转中心的坐标为_________.14.如图,将绕点O逆时针旋转后得到,若恰好经过点A,且,则的度数为_____________.15.如图,在Rt△ABC中,∠ACB=90°,,点D为AB的中点,点P在AC上,且CP=1,将CP绕点C在平面内旋转,点P的对应点为点Q,连接AQ,DQ.当∠ADQ=90°时,AQ的长为______.16.如图,在中,,,,将绕顶点,按顺时针方向旋转到处,此时线段与的交点恰好为的中点,,则线段的长度为______.17.如图,在正方形网格中,线段AB绕某点顺时针旋转角α(0<α<180...