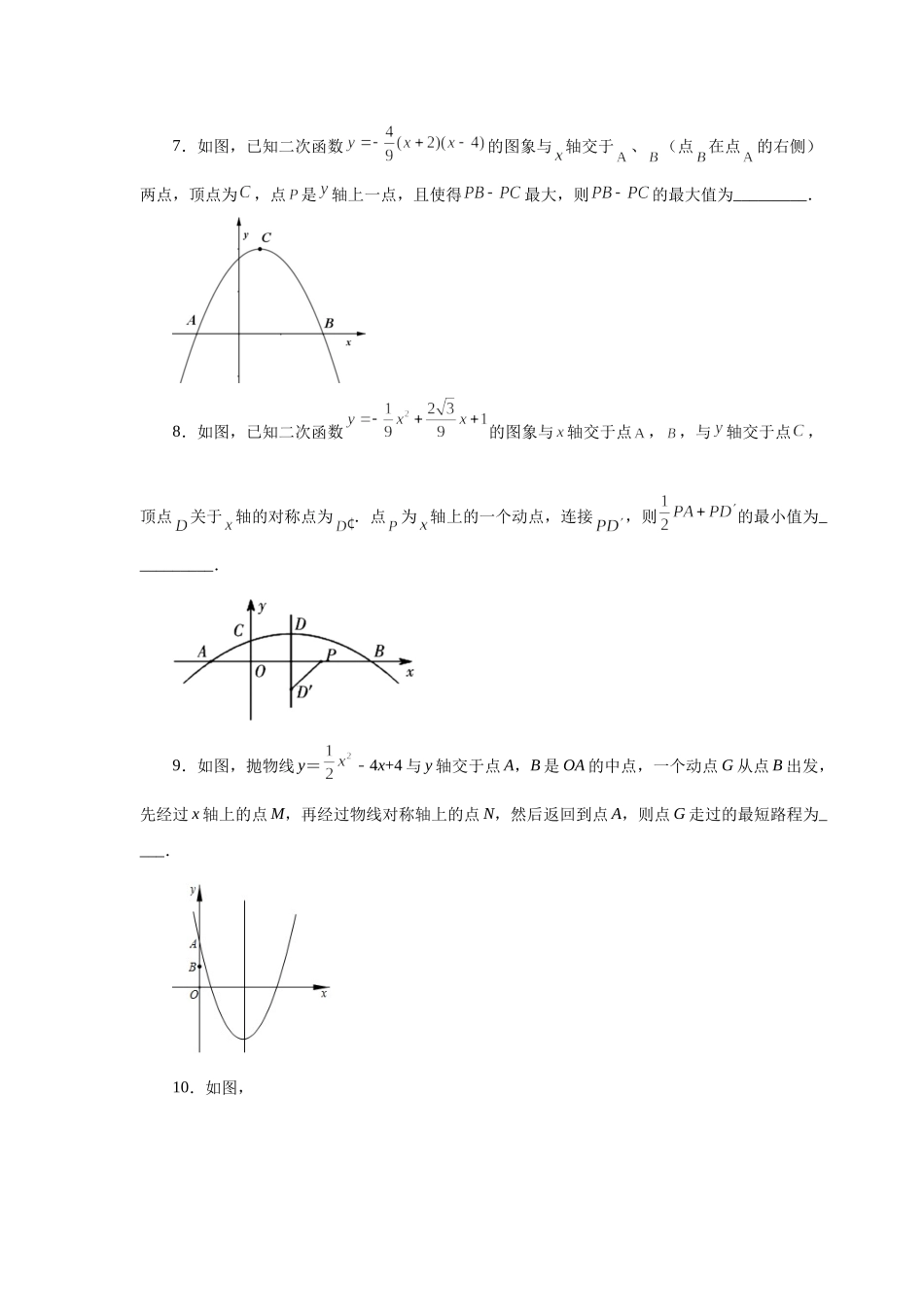
专题22.27二次函数“将军饮马”问题(巩固篇)(专项练习)一、单选题1.如图,抛物线与直线交于两点,点为轴上点,当周长最短时;周长的值为()A.B.C.D.二、填空题2.已知二次函数的图象与轴分别交于、两点,如图所示,与轴交于点,点是其对称轴上一动点,当取得最小值时,点的纵坐标与横坐标之和为______.3.已知抛物线y=ax2+bx+c的图象与x轴交于点A(m4﹣,0)和B(m,0),与直线y=﹣x+p相交于点A和C(2m4﹣,m6)﹣,抛物线y=ax2+bx+c与y轴交于点D,点P在抛物线的对称轴上,连PA,PD,当PA+PD的长最短时,点P的坐标为_____.4.如图抛物线与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为______.5.如图,已知点B(3,3)、C(0,6)是抛物线()上两点,A是抛物线的顶点,P点是轴上一动点,当PA+PB最小时,P点的坐标是_____.6.如图,抛物线y=x﹣2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:①当x>0时,y>0;②若a=1﹣,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6.其中真命题的序号是____________.7.如图,已知二次函数的图象与轴交于、(点在点的右侧)两点,顶点为,点是轴上一点,且使得最大,则的最大值为_________.8.如图,已知二次函数的图象与轴交于点,,与轴交于点,顶点关于轴的对称点为.点为轴上的一个动点,连接,则的最小值为__________.9.如图,抛物线y=﹣4x+4与y轴交于点A,B是OA的中点,一个动点G从点B出发,先经过x轴上的点M,再经过物线对称轴上的点N,然后返回到点A,则点G走过的最短路程为____.10.如图,过抛物线上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣1,在AB上任取一点P,连结OP,作点C关于直线OP的对称点D,连结BD,则线段BD的最小值为______.11.已知中,边的长与边上的高的和为,当面积最大时,则其周长的最小值为________(用含的代数式表示).三、解答题12.已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.(1)求抛物线的解析式;(2)抛物线的对称轴上有一动点P,求△PAD周长的最小值.13.如图,抛物线与x轴交...