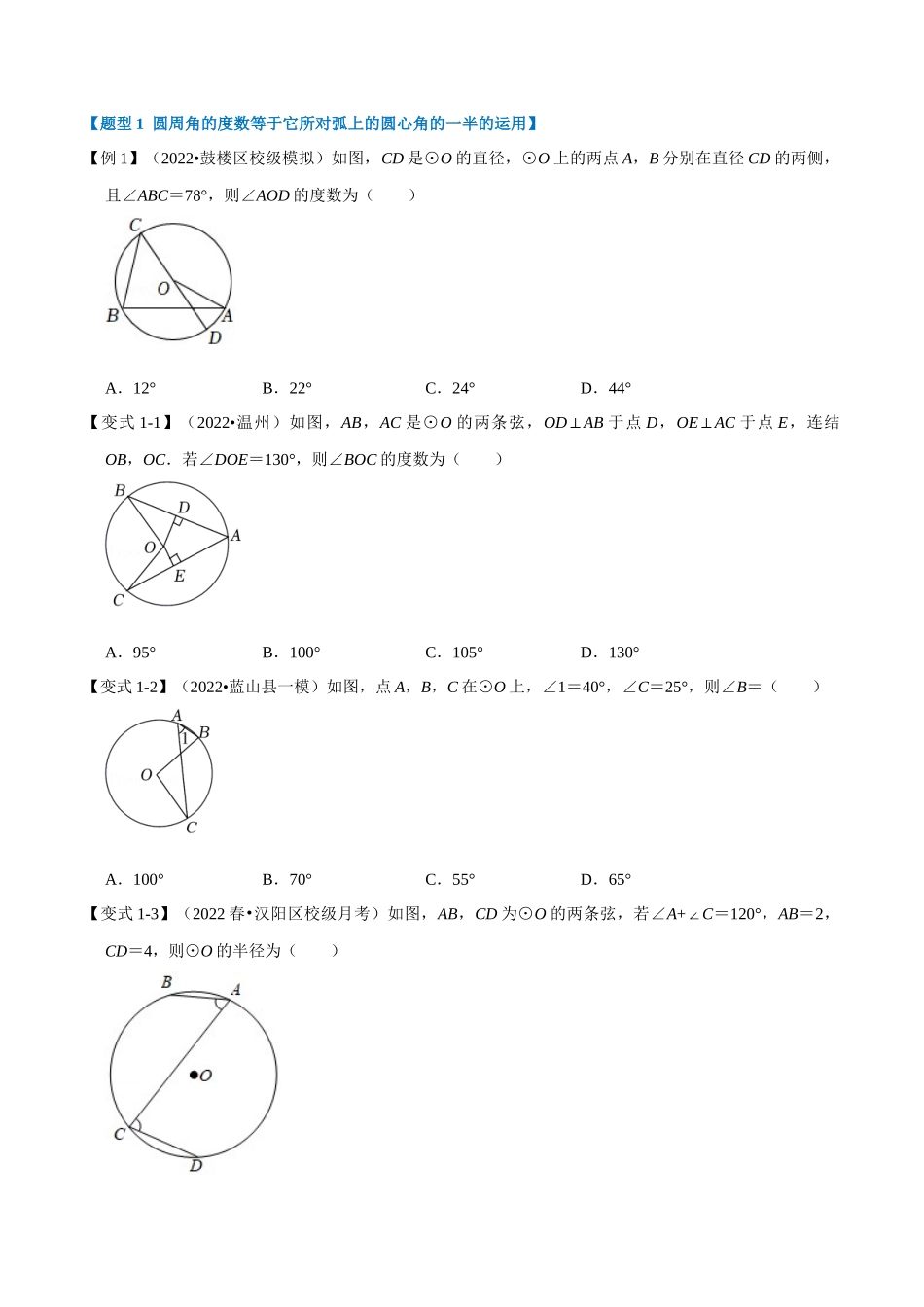
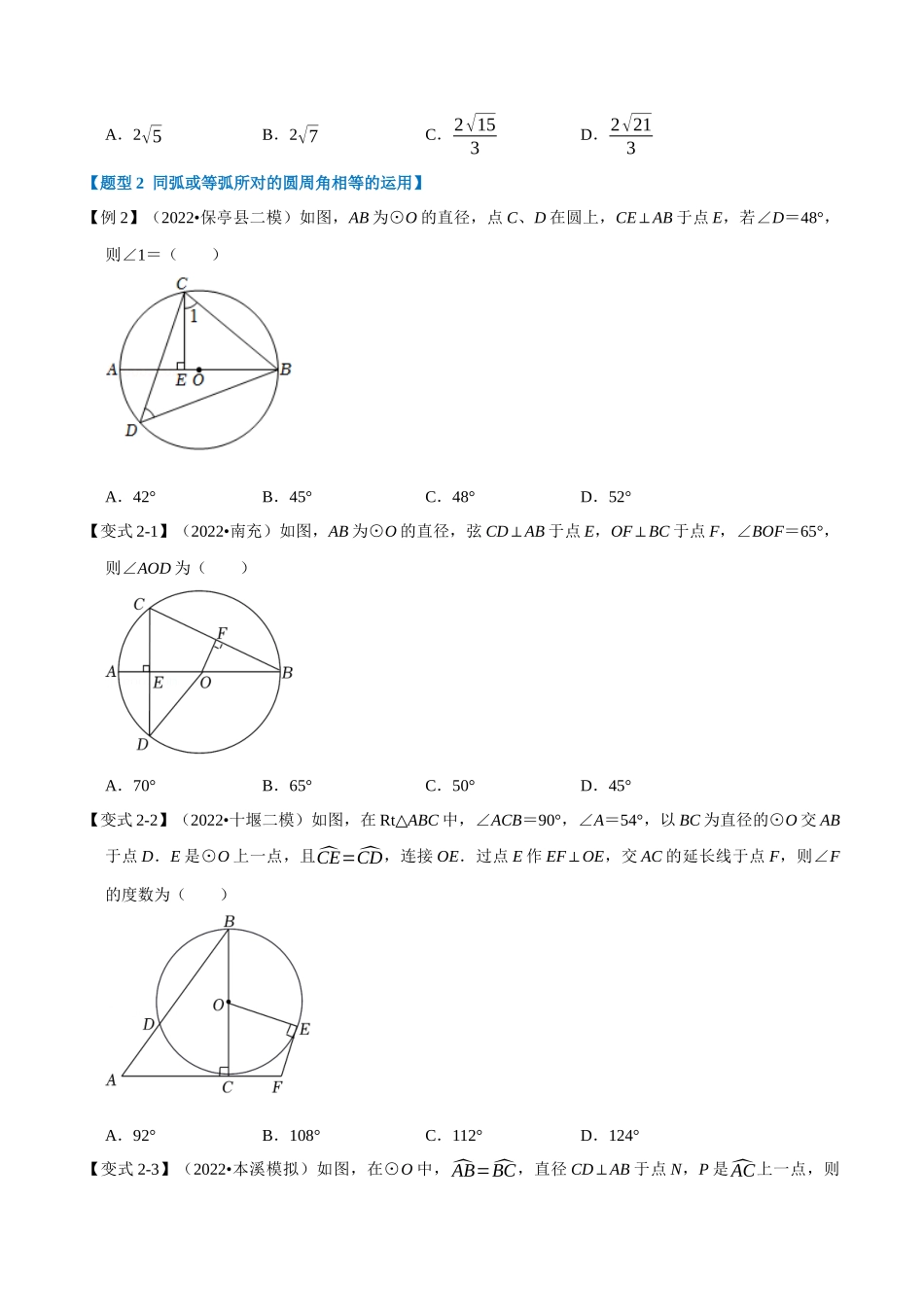
专题24.4 圆周角定理【十大题型】（人教版）（原卷版）.docx

专题24.4 圆周角定理【十大题型】 【人教版】 【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】 2 【题型2 同弧或等弧所对的圆周角相等的运用】 5 【题型3 直径所对的圆周角是90°的运用】 9 【题型4 翻折中的圆周角的运用】 13 【题型5 利用圆周角求最值】 18 【题型6 圆周角中的证明】 22 【题型7 圆周角中的多结论问题】 28 【题型8 构造圆利用圆周角解决三角形或四边形中的问题】 32 【题型9 圆周角与量角器的综合运用】 37 【题型10 利用圆周角求取值范围】 40 【知识点1 圆周角定理及其推论】 圆周角定理 定理：圆周角的度数等于它所对的弧的圆心角度数的一半 是所对的圆心角， 是所对的圆周角， 推论1：同弧或等弧所对的圆周角相等 和都是所对的圆周角 推论2：直径所对的圆周角是直角，的圆周角所对的弦是直径 是的直径 是所对的圆周角 是所对的圆周角 是的直径 【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】 【例1】（2022•鼓楼区校级模拟）如图，CD是⊙O的直径，⊙O上的两点A，B分别在直径CD的两侧，且∠ABC＝78°，则∠AOD的度数为（　　） A．12° B．22° C．24° D．44° 【变式1-1】（2022•温州）如图，AB，AC是⊙O的两条弦，OD⊥AB于点D，OE⊥AC于点E，连结OB，OC．若∠DOE＝130°，则∠BOC的度数为（　　） A．95° B．100° C．105° D．130° 【变式1-2】（2022•蓝山县一模）如图，点A，B，C在⊙O上，∠1＝40°，∠C＝25°，则∠B＝（　　） A．100° B．70° C．55° D．65° 【变式1-3】（2022春•汉阳区校级月考）如图，AB，CD为⊙O的两条弦，若∠A+∠C＝120°，AB＝2，CD＝4，则⊙O的半径为（　　） A．25 B．27 C．2153 D．2213 【题型2 同弧或等弧所对的圆周角相等的运用】 【例2】（2022•保亭县二模）如图，AB为⊙O的直径，点C、D在圆上，CE⊥AB于点E，若∠D＝48°，则∠1＝（　　） A．42° B．45° C．48° D．52° 【变式2-1】（2022•南充）如图，AB为⊙O的直径，弦CD⊥AB于点E，OF⊥BC于点F，∠BOF＝65°，则∠AOD为（　　） A．70° B．65° C．50° D．45° 【变式2-2】（2022•十堰二模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝54°，以BC为直径的⊙O交AB于点D．E是⊙O上一点，且CE=CD，连接OE．过点E作EF⊥OE，交AC的延长线于点F，则∠F的度数为（　　） A．92° B．108° C．112° D．124° 【变式2-3】（2022•本溪模拟）如图，在⊙O中，AB=BC，直径CD⊥AB于点N，P是AC上一点，则∠BPD的度数是 　 　． 【题型3 直径所对的圆周角是90°的运用】 【例3】（2022•中山市三模）如图，AB是⊙O的直径，若AC＝2，∠D＝60°，则BC长等于（　　） A．4 B．5 C．3 D．23 【变式3-1】（2022•潍坊二模）如图，已知以△ABC的边AB为直径的⊙O经过点C，OD⊥AC交⊙O于点D，连接BD．若∠BAC＝36°，则∠ODB的度数为（　　） A．32° B．27° C．24° D．18° 【变式3-2】（2022•江夏区校级开学）如图，⊙O的直径AB为8，D为AC上的一点，DE⊥AC于点E，若CE＝3AE，∠BAC＝30°，则DE的长是（　　） A．85 B．13−2 C．3 D．32 【变式3-3】（2022秋•如皋市校级期中）在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连接CD． （1）如图1，若点D与圆心O重合，AC＝2，求⊙O的半径r； （2）如图2，若点D与圆心O不重合，∠BAC＝25°，求∠DCA的度数． 【题型4 翻折中的圆周角的运用】 【例4】（2022春•福田区校级月考）如图，AB是⊙O的直径，BC是⊙O的弦，先将BC沿BC翻折交AB于点D，再将BD沿AB翻折交BC于点E．若BE=DE，则∠BCD的度数是（　　） A．22.5° B．30° C．45° D．60° 【变式4-1】（2022秋•萧山区期中）如图，在⊙O中，AB为直径，点C为圆上一点，将劣弧AC沿弦AC翻折交AB于点D，连结CD，若∠BAC＝25°，则∠BDC的度数为（　　） A．45° B．55° C．65° D．70° 【变式4-2】（2022秋•硚口区期末）如图，AB为⊙O的一条弦，C为⊙O上一点，OC∥AB．将劣弧AB沿弦AB翻折，交翻折后的弧AB交AC于点D．若D为翻折后弧AB的中点，则∠ABC＝（　　） A．110° B．112.5° C．115° D．117.5° 【变式4-3】（2022秋•丹江口市期中）已知⊙O的直径AB长为10，弦CD⊥AB，将⊙O沿CD翻折，翻折后点B的对应点为点B′，若AB′＝6，CB′的长为（　　） A．45 B．25或45 C．25 D．25或43 【题型5 利用圆周角求最值】 【例5】（2022•瑶海区三模）如图，AB是⊙O的直径，AB＝8，点M在⊙O上，∠MAB＝20°，N是弧MB的中点，P是直径AB上的一动点，若MN＝2，则△PMN周长的最小值为（　　） A．4 B．5 C．6 D．7 【变式5-1】（2022•陈仓区一模）如图，△ABC中，∠ABC＝45°，∠ACB＝75°，AB＝4，D是边BC上的一个动点，以AD为直径画⊙O，分别交AB、AC于点E、F，连接EF，则线段EF长度的最小值为 　 　． 【变式5-2】（2022秋•大连期末）如图，AB是⊙O的直径，AB＝2，点C在⊙O上，∠CAB＝30°，D为BC的中点，E是直径AB上一动点，则CE+DE最小值为（　　） A．1 B．2 C．3 D．2 【变式5-3】（2022•杏花岭区校级三模）如图，矩形ABCD中，AB=32，BC＝AB2，E为射线BA上一动点，连接CE交以BE为直径的圆于点H，则线段DH长度的最小值为　 ． 【题型6 圆周角中的证明】 【例6】（2022秋•定陶区期末）如图1．在⊙O中AB＝AC，∠ACB＝70°，点E在劣弧AC上运动，连接EC，BE，交AC于点F． （1）求∠E的度数； （2）当点E运动到使BE⊥AC时，连接AO并延长，交BE于点D，交BC于点G，交⊙O于点M，依据题意在备用图中画出图形．并证明：G为DM的中点． 【变式6-1】（2022春•金山区校级月考）已知CD为⊙O的直径，A、B为⊙O上两点，点C为劣弧AB中点，连接DA、BA、AC，且∠B＝30°． （1）求证：∠D＝30°； （2）F、G分别为线段CD、AC上两点，满足DF＝AG，连接AF、OG，取OG中点H，连接CH，请猜测AF与CH之间的数量关系，并证明． 【变式6-2】（2022•武汉）如图，以AB为直径的⊙O经过△ABC的顶点C，AE，BE分别平分∠BAC和∠ABC，AE的延长线交⊙O于点D，连接BD． （1）判断△BDE的形状，并证明你的结论； （2）若AB＝10，BE＝210，求BC的长． 【变式6-3】（2022•南召县四模）阅读下面材料，完成相应的任务： 阿基米德是有史以来最伟大的数学家之一、《阿基米德全集》收集了已发现的阿基米德著作，它对于了解古希腊数学，研究古希腊数学思想以及整个科技史都是十分宝贵的．其中论述了阿基米德折弦定理：从圆周上任一点出发的两条弦，所组成的折线，称之为该圆的一条折弦．一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影，就是折弦的中点． 如图1，AB和BC是⊙O的两条弦（即ABC是圆的一条折弦），BC＞AB．M是弧ABC的中点，则从M向BC所作垂线之垂足D是折弦ABC的中点，即CD＝AB+BD． 小明认为可以利用“截长法”，如图2：在线段CB上从C点截取一段线段CN＝AB，连接MA，MB，MC，MN． 小丽认为可以利用“垂线法”，如图3：过点M作MH⊥AB于点H，连接MA，MB，MC． 任务：（1）请你从小明和小丽的方法中任选一种证明思路，继续书写出证明过程． （2）就图3证明：MC2﹣MB2＝BC•AB． 【题型7 圆周角中的多结论问题】 【例7】（2022•兰陵县二模）如图，在⊙O中，AB是⊙O的直径，AB＝10，AC=CD=DB，点E是点D关于AB的对称点，M是AB上的一动点，下列结论： ①∠BOE＝30°；②∠DOB＝2∠CED；③DM⊥CE；④CM+DM的最小值是10，上述结论中正确的个数是（　　） A．1 B．2 C．3 D．4 【变式7-1】（2022秋•淅川县期末）如图，已知：点A、B、C、D在⊙O上，AB＝CD，下列结论：①∠AOC＝∠BOD；②∠BOD＝2∠BAD；③AC＝BD；④∠CAB＝∠BDC；⑤∠CAO+∠CDO＝180°．其中正确的个数为（　　） A．2 B．3 C．4 D．5 【变式7-2】（2022秋•厦门期末）在△ABC中，AB＝AC，以AB为直径的⊙O交BC边于点D．要使得⊙O与AC边的交点E关于直线AD的对称点在线段OA上（不与端点重合），需满足的条件可以是 　 ．（写出所有正确答案的序号） ①∠BAC＞60°；②45°＜∠ABC＜60°；③BD＞12AB；④12AB＜DE＜22AB． 【变式7-3】（2022秋•东台市月考）如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD与BC，OC分别相交于点E，F，则下列结论：①AD⊥BD；②∠AOC＝∠AEC；③CB平分∠ABD；④AF＝DF；⑤△CEF≌△BED．其中一定成立的结论是　 　．（填序号） 【题型8 构造圆利用圆周角解决三角形或四边形中的问题】 【例8】（2022春•杏花岭区校级月考）如图，A，B两点的坐标分别为（﹣2，0），（3，0），点C在y轴正半轴上，且∠ACB＝45°，则点C的坐标为（　　） A．（0，7） B．（0，210） C．（0，6） D．（0，35） 【变式8-1】（2022秋•秦淮区期末）如图，在四边形ABCD中，AB＝BC＝BD．若∠ABC＝112°，则∠ADC＝　 　°． 【变式8-2】（2022•北京模拟）已知三角形ABC是锐角三角形，其中∠A＝30°，BC＝4，设BC边上的高为h，则h的取值范围是 　 ． 【变式8-3】（2022春•西湖区校级月考）已知：如图，四边形ABCD中，AD∥BC，AB＝BC＝4，∠B＝60°，∠C＝105°，点E为BC的中点，以CE为弦作圆，设该圆与四边形ABCD的一边的交点为P，若∠CPE＝30°，则EP的长为　 　． 【题型9 圆周角与量角器的综合运用】 【例9】（2022•南召县模拟）以O为中心点的量角器与直角三角板ABC按如图方式摆放，量角器的0刻度线与斜边AB重合．点D为斜边AB上一点，作射线CD交弧AB于点E，如果点E所对应的读数为50°，那么∠BDE的大小为（　　） A．100° B．110° C．115° D．130° 【变式9-1】（2022秋•南京期中）将量角器按如图所示的方式放置在三角形纸片上，使点O在半圆圆心上，点B在半圆上，边AB，AO分别交半圆于点C，D，点B，C，D对应的读数分别为160°、72°、50°，则∠A＝　 　． 【变式9-2】（2022秋•高港区期中）如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应的刻度值为50°，则∠BCD的度数为 　 ． 【变式9-3】（2022秋•北京期末）如图，量角器的直径与直角三角尺ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转，CP与量角器的半圆弧交于点E，则第20秒点E在量角器上对应的读数是　 °． 【题型10 利用圆周角求取值范围】 【例10】（2022•观山湖区模拟）如图，OB是⊙O的半径，弦AB＝OB，直径CD⊥AB．若点P是线段OD上的动点，点P不与O，D重合，连接PA．设∠PAB＝β，则β的取值范围是　 　． 【变式10-1】（2022•河南三模）如图，点O是以AC为直径的半圆的圆心，点B在AC上，∠ACB＝30°，AC＝2．点D是直径AC上一动点（与点A，C不重合），记OD的长为m．连接BD，点A关于BD的对称点为点A′，当点A′落在由直径AC，弦AB，BC围成的封闭图形内部时（不包含边界），m的取值范围是 　 　． 【变式10-2】（2022秋•台州期中）如图，已知AB是⊙O的一条弦，点C是⊙O的优弧ACB上的一个动点（不与A，B不重合）， （1）设∠ACB的平分线与劣弧AB交于点P，试猜想点P劣弧AB上的位置是否会随点C的运动而变化？请说明理由 （2）如图②，设AB＝8，⊙O的半径为5，在（1）的条件下，四边形ACBP的面积是否为定值？若是定值，请求出这个定值；若不是定值，请求出ACBP的面积的取值范围． 【变式10-3】（2022秋•高新区校级期末）如图，A、B为⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合），我们称∠APB是⊙O上关于A、B的滑动角．若⊙O的半径是1，2≤AB≤3，则∠APB的取值范围为　 　．