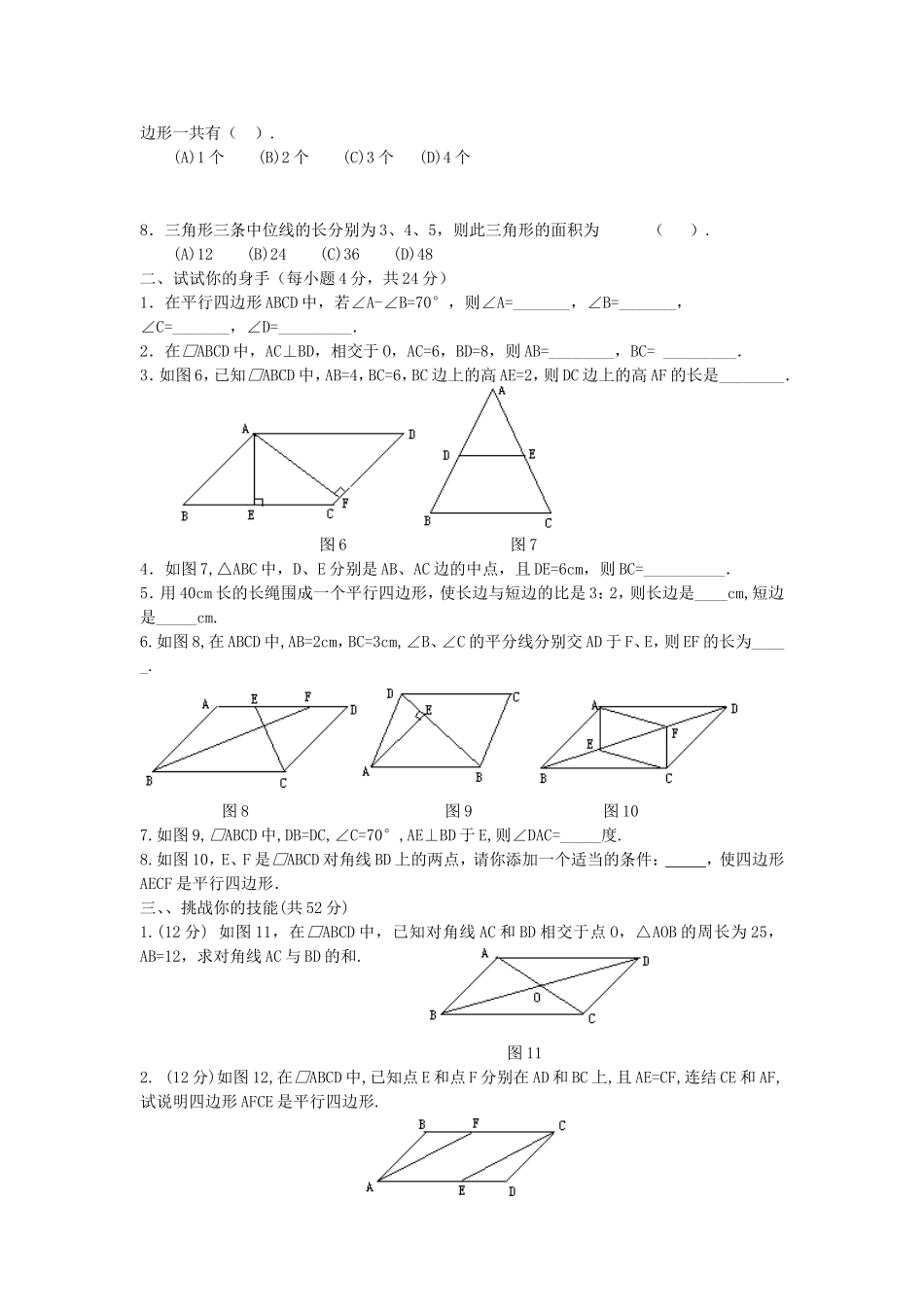
数学:19.1平行四边形同步测试题B(人教新课标八年级下)A组一、相信你的选择(每小题4分,共24分)1.如图1,在平行四边形ABCD中,下列各式不一定正确的是().(A)18021(B)18032(C)18043(D)18042图1图22.如图2,在□ABCD中,EF//AB,GH//AD,EF与GH交于点O,则该图中的平行四边形的个数共有().(A)7个(B)8个(C)9个(D)11个3.(08贵阳市)如图,在平行四边形中,是延长线上的一点,若,则的度数为()A.B.C.D.Error:Referencesourcenotfound4.下列说法,属于平行四边形判别方法的有()个.①两组对边分别平行的四边形;②平行四边形的对角线互相平分;③两组对边分别相等的四边形;④平行四边形的每组对边平行且相等;⑤两条对角线互相平分的四边形是平行四边形;⑥一组对边平行且相等的四边形是平行四边形.(A)6个(B)5个(C)4个(D)3个5.如图3,在□ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F的值为().(A)110°(B)30°(C)50°(D)70°图3图46.如图4,□ABCD中,对角线AC,BD相交于点O,将△AOD平移至△BEC的位置,则图中与OA相等的其它线段有().(A)1条(B)2条(C)3条(D)4条7.如图5,点D、E、F分别是AB、BC、CA边的中点,则图中的平行四图5边形一共有().(A)1个(B)2个(C)3个(D)4个8.三角形三条中位线的长分别为3、4、5,则此三角形的面积为().(A)12(B)24(C)36(D)48二、试试你的身手(每小题4分,共24分)1.在平行四边形ABCD中,若∠A-∠B=70°,则∠A=_______,∠B=_______,∠C=_______,∠D=_________.2.在□ABCD中,AC⊥BD,相交于O,AC=6,BD=8,则AB=________,BC=_________.3.如图6,已知□ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是________.图6图74.如图7,△ABC中,D、E分别是AB、AC边的中点,且DE=6cm,则BC=__________.5.用40cm长的长绳围成一个平行四边形,使长边与短边的比是3:2,则长边是____cm,短边是_____cm.6.如图8,在ABCD中,AB=2cm,BC=3cm,∠B、∠C的平分线分别交AD于F、E,则EF的长为_____.图8图9图107.如图9,□ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAC=_____度.8.如图10,E、F是□ABCD对角线BD上的两点,请你添加一个适当的条件:,使四边形AECF是平行四边形.三、、挑战你的技能(共52分)1.(12分)如图11,在□ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为25,AB=12,求对角线AC与BD的和.图112.(12分)如图12,在□ABCD中,已知点...