第20章 数据的分析（22页）.doc

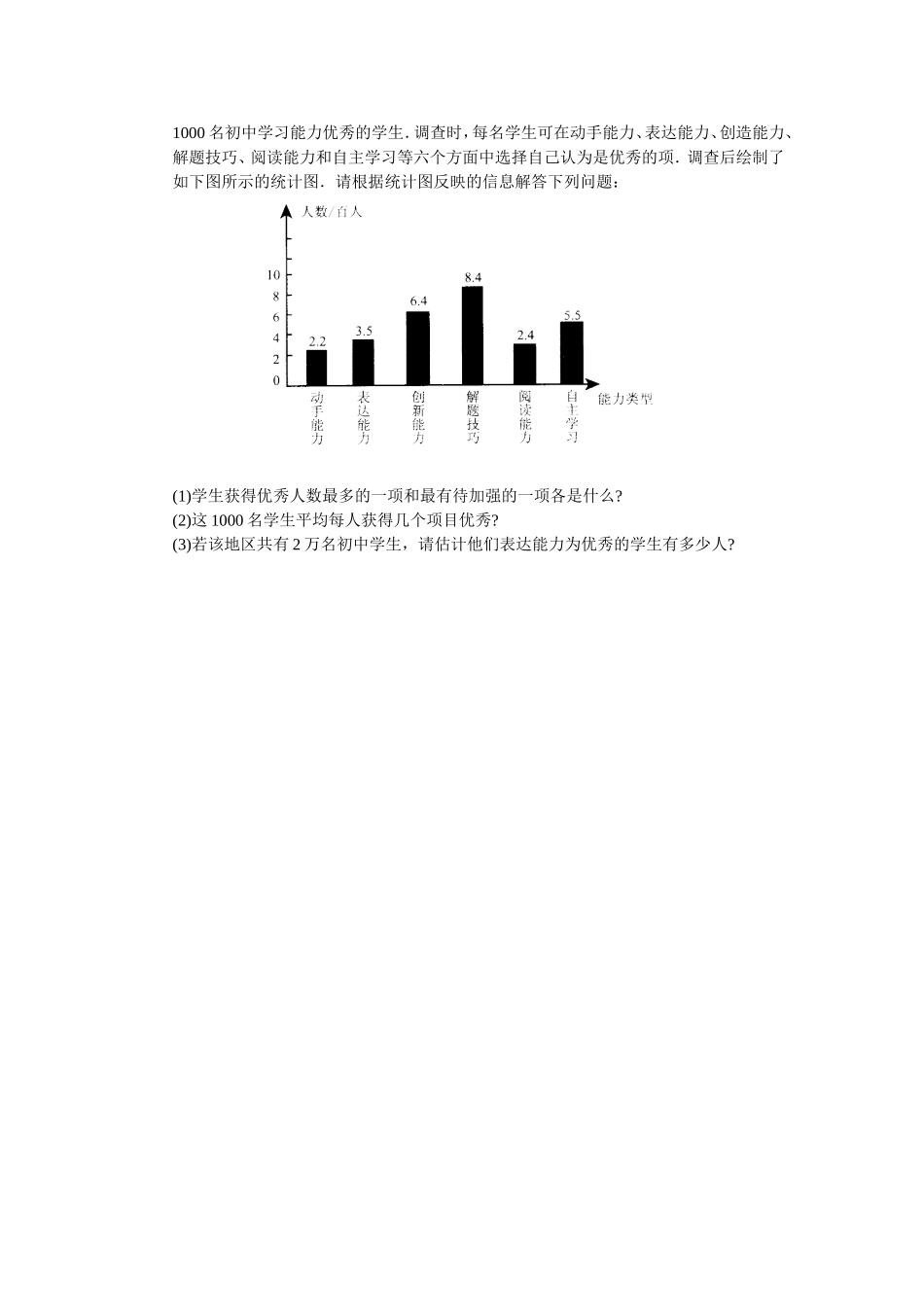
第二十章 数据的分析 测试1 平均数(一) 学习要求 了解加权平均数的意义和求法，会求实际问题中一组数据的平均数． 课堂学习检测 一、填空题 1．一组数据中有3个7，4个11和3个9，那么它们的平均数是______． 2．某组学生进行“引体向上”测试，有2名学生做了8次，其余4名学生分别做了10次、7次、6次、9次，那么这组学生的平均成绩为______次，在平均成绩之上的有______人． 3．某校一次歌咏比赛中，7位评委给8年级(1)班的歌曲打分如下：9.65，9.70，9.68，9.75，9.72，9.65，9.78，去掉一个最高分，再去掉一个最低分，计算平均分为该班最后得分，则8年级(1)班最后得分是______分． 二、选择题 4．如果数据2，3，x，4的平均数是3，那么x等于( )． (A)2 (B)3 (C)3.5 (D)4 5．某居民大院月底统计用电情况，其中3户用电45度，5户用电50度，6户用电42度，则每户平均用电( )． (A)41度 (B)42度 (C)45.5度 (D)46度 三、解答题 6．甲、乙两支仪仗队队员的身高(单位：厘米)如下： 甲队：178 177 179 178 177 178 177 179 178 179； 乙队：178 179 176 178 180 178 176 178 177 180． (1)将下表填完整： 身高(厘米) 176 177 178 179 180 甲队(人数) 3 4 0 乙队(人数) 2 1 1 (2)甲队队员身高的平均数为______厘米，乙队队员身高的平均数为______厘米； (3)你认为哪支仪仗队更为整齐?简要说明理由． 7．小明和小颖本学期数学平时成绩、期中成绩、期末成绩分别如下： 平时 期中 期末 小明 85 90 92 小颖 90 83 88 假如学期总评按平时成绩、期中成绩、期末成绩各占1∶3∶6的比例来计算，那么小明和小颖的学期总评成绩谁较高? 综合、运用、诊断 一、填空题 8．某公园对游园人数进行了10天统计，结果有4天是每天900人游园，有2天是每天1100人游园，有4天是每天800人游园，那么这10天平均每天游园人数是______人． 9．如果10名学生的平均身高为1.65米，其中2名学生的平均身高为1.75米，那么余下8名学生的平均身高是______米． 10．某校规定学生的学期体育成绩由三部分组成：体育课外活动占学期成绩的10％，理论测试占30％，体育技能测试占60％，一名同学上述三项成绩依次为90，92，73分，则这名同学本学期的体育成绩为______分，可以看出，三项成绩中______的成绩对学期成绩的影响最大． 二、选择题 11．为了解乡镇企业的水资源的利用情况，市水利管理部门抽查了部分乡镇企业在一个月中的用水情况，其中用水15吨的有3家，用水20吨的有5家，用水30吨的有7家，那么平均每家企业1个月用水( )． (A)23.7吨 (B)21.6吨 (C)20吨 (D)5.416吨 12．m个x1，n个x2和r个x3，由这些数据组成一组数据的平均数是( )． (A) (B) (C) (D) 三、解答题 13．从1月15日起，小明连续8天每天晚上记录了家中天然气表显示的读数(如下表)： 日期 15日 16日 17日 18日 19日 20日 21日 22日 天然气表读数(单位：m3) 220 229 241 249 259 270 279 290 小明的父亲买了一张面值600元的天然气使用卡，已知天然气每立方米1.70元，请估计这张卡是否够小明家用一个月(按30天计算)，将结果填在后面的横线上．(只填“够”或“不够”)结果为：______．并说明为什么． 14．四川汶川大地震发生后，某中学八年级(1)班共有40名同学参加了“我为灾区献爱心”的活动．活动结束后，生活委员小林将捐款情况进行了统计，并绘制成如右的统计图． (1)求这40名同学捐款的平均数； (2)该校共有学生1200名，请根据该班的捐款情况，估计这个中学的捐款总数大约是多少元? 15．某地为了解从2004年以来初中学生参加基础教育课程改革的情况，随机调查了本地区1000名初中学习能力优秀的学生．调查时，每名学生可在动手能力、表达能力、创造能力、解题技巧、阅读能力和自主学习等六个方面中选择自己认为是优秀的项．调查后绘制了如下图所示的统计图．请根据统计图反映的信息解答下列问题： (1)学生获得优秀人数最多的一项和最有待加强的一项各是什么? (2)这1000名学生平均每人获得几个项目优秀? (3)若该地区共有2万名初中学生，请估计他们表达能力为优秀的学生有多少人? 测试2 平均数(二) 学习要求 加强实际问题中平均数的计算，体会用样本平均数估计总体平均数的思想． 课堂学习检测 一、填空题 1．已知7，4，5和x的平均数是5，则x＝______． 2．某校12名同学参加数学科普活动比赛，其中8名男同学的平均成绩为85分，其余的女同学的平均成绩为76分，则该校12名同学的平均成绩为______分． 3．某班50名学生平均身高168cm，其中30名男生平均身高170cm，则20名女生的平均身高为______cm． 二、选择题 4．如果a、b、c的平均数是4，那么a－1，b－5和c＋3的平均数是( )． (A)－1 (B)3 (C)5 (D)9 5．某班一次知识问答成绩如下： 成绩/分 50 60 70 80 90 100 人数/人 1 3 8 17 14 7 那么这次知识问答全班的平均成绩是( )(结果保留整数)． (A)80分 (B)81分 (C)82分 (D)83分 三、解答题 6．某班有学生52人，期末数学考试平均成绩是72分．有两名同学下学期要转学，已知他俩的成绩分别为70分和80分．求他俩转学后该班的数学平均分． 7．某瓜农采用大棚栽培技术种植了1亩地的两种西瓜，共产出了约600个西瓜．在西瓜上市前，该瓜农随机摘下了10个成熟的西瓜称重： 西瓜质量/千克 5.5 5.4 5.0 4.9 4.6 4.3 西瓜数量/个 1 2 3 2 1 1 计算这10个西瓜的平均质量，并估计这1亩地的西瓜产量是多少千克． 综合、运用、诊断 一、填空题 8．如果一组数据中有3个6、4个－1，2个－2、1个0和3个x，其平均数为x，那么x＝ ______． 9．某次射击训练中，一小组的成绩如下表所示： 环数/环 6 7 8 9 人数/人 1 3 2 若该小组的平均成绩为7.7环，则成绩为8环的人数是______． 二、选择题 10．一次考试后，某学习小组组长算出全组5位同学数学的平均分为M，如果把M当成另一个同学的分数，与原来的5个分数一起，算出这6个分数的平均数为N，那么M∶N为( )． (A)5∶6 (B)1∶1 (C)6∶5 (D)2∶1 11．某辆汽车从甲地以速度v1匀速行驶至乙地后，又从乙地以速度v2匀速返回甲地，则汽车在这个行驶过程中的平均速度是( )． (A) (B) (C) (D) 12．某同学在用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此算出的平均数与实际平均数的差为( )． (A)3 (B)－3 (C)3.5 (D)－3.5 三、解答题 13．我国从2008年6月1日起执行“限塑令”．“限塑令”执行前，某校为了了解本校学生所在家庭使用塑料袋的数量情况，随机调查了10名学生所在家庭每月使用塑料袋的数量，结果如下(单位：只) 65 70 85 75 79 74 91 81 95 85 (1)计算这10名学生所在家庭平均每月使用塑料袋多少只? (2)“限塑令”执行后，家庭每月使用塑料袋数量预计将减少50％．根据上面的计算结果，估计该校1000名学生所在家庭每月使用塑料袋可减少多少只? 拓展、探究、思考 一、解答题 14．某中学为了了解本校学生的身体发育情况，抽测了同年龄的40名女学生的身高情况，统计人员将上述数据整理后，列出了频数分布表如下： 身高(cm) 频数 144.5＜x≤149.5 2 149.5＜x≤154.5 A 154.5＜x≤159.5 14 159.5＜x≤164.5 12 164.5＜x≤169.5 6 合计 40 根据以上信息回答下列问题： (1)频数分布表中的A＝______； (2)这40名女学生的平均身高是______cm(精确到0.1cm)． 15．某人为了了解他所在地区的旅游情况，收集了该地区2004至2007年每年的旅游收入及入境旅游人数(其中缺少2006年入境旅游人数)的有关数据，整理并分别绘成图1，图2． 图1 图2 根据上述信息，回答下列问题： (1)该地区2004至2007年四年的年旅游收入的平均数是______亿元； (2)据了解，该地区2006年、2007年入境旅游人数的年增长率相同，那么2006年入境旅游人数是______万人； (3)根据第(2)小题中的信息，请把图2补画完整． 测试3 中位数和众数(一) 学习要求 了解中位数和众数的意义，掌握它们的求法． 课堂学习检测 一、填空题 1．学校篮球集训队11名队员进行定点投篮训练，将11名队员在1分钟内投进篮筐的球数由小到大排序后为6，7，8，9，9，9，9，10，10，10，12，这组数据的众数和中位数分别是______． 2．资阳市某学校初中2008级有四个绿化小组，在植树节这天种下柏树的棵数如下：10，10，x，8，若这组数据的众数和平均数相等,那么它的中位数是______棵． 3．已知数据1，2，x和5的平均数是2.5，则这组数据的众数是______． 二、选择题 4．对于数据2，4，4，5，3，9，4，5，1，8，其众数、中位数和平均数分别为( )． (A)4 4 6 (B)4 6 4.5 (C)4 4 4.5 (D)5 6 4.5 5．为了筹备班里的新年联欢会，班长以全班同学最爱吃哪几种水果做民意调查，以决定最终买什么水果．该次调查结果最终应该由数据的( )决定． (A)平均数 (B)中位数 (C）众数 (D)无法确定 6．一名射击运动员连续打靶8次，命中的环数如图所示，这组数据的众数与中位数分别为( ) (A)9与8 (B)8与9 (C)8与8 (D)8.5与9 三、解答题 7．公园里有甲、乙两群游客正在进行团体活动，两群游客的年龄如下(单位：岁)： 甲群：13 13 14 15 15 15 1 5 16 17 17； 乙群：3 4 4 5 5 6 6 54 57． 回答下列问题： (1)甲群游客的平均年龄是______岁，中位数是______岁，众数是______，其中______能较好地反映这群游客的年龄特征： (2)乙群游客的平均年龄是______岁，中位数是______岁，众数是______，其中______能较好地反映这群游客的年龄特征． 8．某饮食公司为一学校提供午餐，有3元、4元和5元三种价格的饭菜供师生选择(每人限定一份)．如图，是五月份的销售情况统计图，这个月一共销售了10400份饭菜，那么师生购买午餐费用的平均数、中位数和众数各是多少? 综合、运用、诊断 一、填空题 9．在一次中学生田径运动会上，参加男子跳高的17名运动员的成绩如下： 成绩/米 1.50 1.60 1.65 ⒈70 1.75 1.80 1.85 1.90 人数/人 2 3 2 3 4 1 1 1 那么运动员成绩的众数是______，中位数是______，平均数是______． 10．如果数据20，30，50，90和x的众数是20，那么这组数据的中位数是______，平均数是______． 二、选择题 11．已知数据x，5，0，3，－1的平均数是1，那么它的中位数是( )． (A)0 (B)2.5 (C)1 (D)0.5 12．如果一组数据中有一个数据变动，那么( )． (A)平均数一定会变动 (B)中位数一定会变动 (C)众数一定会变动 (D)平均数、中位数和众数可能都不变 三、解答题 13．某校八年级(1)班50名学生参加2009年贵阳市数学质量监控考试，全班学生的成绩统计如下表： 成绩/分 71 74 78 80 82 83 85 86 88 90 91 92 94 人数/人 1 2 3 5 4 5 3 7 8 4 3 3 2 请根据表中提供的信息解答下列问题： (1)该班学生考试成绩的众数是______； (2)该班学生考试成绩的中位数是______； (3)该班张华同学在这次考试中的成绩是83分，能不能说张华同学的成绩处于全班中游偏上水平?试说明理由． 14．某中学要召开运动会，决定从九年级全部的150名女生中选30人，组成一个花队(要求参加花队的同学的身高尽可能接近)．现在抽测了10名女生的身高，结果如下(单位：厘米)： 166 154 151 167 162 158 158 160 162 162． (1)依据数据估计，九年级全体女生的平均身高约是多少? (2)这10名女生的身高的中位数和众数各是多少? (3)请你依据本数据，设计一个挑选参加花队的女生的方案．(要简要说明) 拓展、探究、思考 一、选择题 15．国家规定“中小学生每天在校体育活动时间不低于1小时”．为此，我市就“你每天在校体育活动时间是多少”的问题随机调查了某区300名初中学生，根据调查结果绘制成的统计图(部分)如图所示，其中分组情况是： A组：t＜0.5h； B组：0.5h≤t＜1h； C组：1h≤t＜1.5h； D组：t≥1.5h． 根据上述信息，你认为本次调查数据的中位数落在( )． (A)B组 (B)C组 (C)D组 (D)A组 二、解答题 16．为了解某校九年级学生体育测试成绩情况，现从中随机抽取部分学生的体育成绩统计如下，其中右侧扇形统计图中的圆心角a 为36°． 体育成绩统计表 体育成绩/分 人数/人 百分比/％ 26 8 16 27 24 28 15 29 30 m 根据上面提供的信息，回答下列问题： (1)写出样本容量、m的值及抽取部分学生体育成绩的中位数； (2)已知该校九年级共有500名学生，如果体育成绩达28分以上(含28分)为优秀，请估计该校九年级学生体育成绩达到优秀的总人数． 测试4 中位数和众数(二) 学习要求 进一步理解平均数、中位数和众数所代表的不同的数据特征． 课堂学习检测 一、填空题 1．在一组数据中，受最大的一个数据值影响最大的数据代表是______． 2．数据2，2，1，5，－1，1的众数和中位数之和是______． 二、选择题 3．某班第一小组7名同学的毕业升学体育测试成绩(满分30分)依次为：25，23，25，23，27，30，25，这组数据的中位数和众数分别是( ) (A)23 25 (B)23 23 (C)25 23 (D)25 25 4．为调查八年级学生完成作业的时间，某校抽查了8名学生完成作业的时间，依次是：75，70，90，70，70，58，80，55(单位：分钟)，那么这组数据的众数、中位数和平均数依次为( )． (A)70 70 71 (B)70 71 70 (C)71 70 70 (D)70 70 70 三、解答题 5．某校九年级举行了一次数学测验，为了估计平均成绩，在619份试卷中抽取一部分试卷的成绩如下：有1人100分，2人90分，12人85分，8人80分，10人75分，5人70分． (1)求出样本平均数、中位数和众数； (2)估计全年级的平均分． 6．某公司33名职工的月工资(单位：元)如下： 职务 董事长 副董事长 董事 总经理 经理 管理员 职员 人数 1 1 2 1 5 3 20 工资 5500 5000 3500 3000 2500 2000 1500 (1)求该公司职工月工资的平均数、中位数和众数； (2)假设副董事长的工资提升到2万元，董事长的工资提升到3万元，那么新的职工月工资的平均数、中位数和众数是什么? (3)你认为哪个统计量更能反映这个公司员工的工资水平?谈一谈你的看法． 综合、运用、诊断 一、填空题 7．已知a＜b＜c＜d，则数据a，a，b，c，d，b，c，c的众数为______，中位数为______，平均数为______． 8．一组数据的中位数是m，众数是n，则将这组数据中每个数都减去a后，新数据的中位数是______，众数是______． 二、选择题 9．有7个数由小到大排列，其平均数是38．如果这组数中前4个数的平均数是33，后4个数的平均数是42，那么这7个数的中位数是( )． (A)34 (B)1 6 (C)38 (D)20 三、解答题 10．文艺会演中，参加演出的10个班各派1名代表担任评委给演出打分，1班和2班的成绩如下： 评委班级 1 2 3 4 5 6 7 8 9 10 1班得分 8 7 7 4 8 7 8 8 8 8 2班得分 7 8 8 10 7 7 8 7 7 7 (1)若根据平均数作为评选标准，两个班谁将获胜?你认为公平吗?为什么? (2)采用怎样的方法，对参赛的班级更为公平?如果采用你提供的方法，两个班谁将获胜? 11．某同学为了完成统计作业,对全校的耗电情况进行调查．他抽查了10天中全校每天的耗电量，数据如下(单位：度)： 度数 90 93 102 113 114 120 天数 1 1 2 3 1 2 (1)写出上表中数据的众数和平均数； (2)由(1)获得的数据，估计该校一个月(按30天计算)的耗电量； (3)若当地每度电的定价是0.5元，写出该校应付的电费y(元)与天数x(取正整数)之间的函数关系式． 拓展、探究、思考 一、解答题 12．在学校组织的“喜迎奥运，知荣明耻．文明出行”的知识竞赛中，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分．学校将某年级的1班和2班的成绩整理并绘制成如下的统计图： 请你根据以上提供的信息解答下列问题： (1)此次竞赛中，2班成绩在C级以上(包括C级)的人数为______； (2)请你将表格补充完整： 平均数/分 中位数/分 众数/分 1班 87.6 90 2班 87.6 100 (3)请从下列不同角度对这次竞赛成绩的结果进行分析： ①从平均数和中位数的角度来比较1班和2班的成绩； ②从平均数和众数的角度来比较1班和2班的成绩； ③从B级以上(包括B级)的人数的角度来比较1班和2班的成绩． 测试5 极差和方差(一) 学习要求 了解极差和方差的意义和求法，体会它们刻画数据波动的不同特征． 课堂学习检测 一、填空题 1．一组数据100，97，99，103，101中，极差是______，方差是______． 2．数据1，3，2，5和x的平均数是3，则这组数据的方差是______． 3．一个样本的方差[(x1－3)2＋(x2－3)2＋…＋(xn－3)2]，则样本容量是______，样本平均数是______． 二、选择题 4．一组数据－1，0，3，5，x的极差是7，那么x的值可能有( )． (A)1个 (B)2个 (C)4个 (D)6个 5．已知样本数据1，2，4，3，5，下列说法不正确的是( )． (A)平均数是3 (B)中位数是4 (C)极差是4 (D)方差是2 三、解答题 6．甲、乙两组数据如下： 甲组：10 9 11 8 12 13 10 7； 乙组：7 8 9 10 11 12 11 12． 分别计算出这两组数据的极差和方差，并说明哪一组数据波动较小． 7．为检测一批橡胶制品的弹性，现抽取15条皮筋的抗拉伸程度的数据(单位：牛)： 5 4 4 4 5 7 3 3 5 5 6 6 3 6 6 (1)这批橡胶制品的抗拉伸程度的极差为______牛； (2)若生产产品的抗拉伸程度的波动方差大于1.3，这家工厂就应对机器进行检修，现在这家工厂是否应检修生产设备?通过计算说明． 综合、运用、诊断 一、填空题 8．随机从甲、乙两块试验田中各抽取100株麦苗测量高度，计算平均数和方差的结果： ＝13，＝13，＝3.6，＝15.8，则小麦长势比较整齐的试验田是______． 9．把一组数据中的每个数据都减去同一个非零数，则平均数______，方差______．(填“改变”或“不变”) 二、选择题 10．关于数据－4，1，2，－1，2，下面结果中，错误的是( )． (A)中位数为1 (B)方差为26 (C)众数为2 (D)平均数为0 11．某工厂共有50名员工，他们的月工资方差是s2，现在给每个员工的月工资增加200元，那么他们的新工资的方差( )． (A)变为s2＋200 (B)不变 (C)变大了 (D)变小了 12．数据－1，0，3，5，x的极差为7，那么x等于( )． (A)6 (B)－2 (C)6或－2 (D)不能确定 三、解答题 13．甲、乙两个组各10名同学进行英语口语会话测试，每个人测试5次，每个同学合格的次数分别如下： 甲组：4 1 2 2 1 3 3 1 2 1； 乙组：4 3 0 2 1 3 3 0 1 3． (1)如果合格3次以上(含3次)为及格标准，请你说明哪个小组的及格率高； (2)请你比较两个小组口语会话的合格次数谁比较稳定． 测试6 极差和方差(二) 学习要求 体会用样本方差估计总体方差的思想，掌握分析数据的思想和方法． 课堂学习检测 一、选择题 1．如图是根据某地2008年4月上旬每天最低气温绘成的折线图，那么这段时间最低气温的极差、众数、平均数依次是( )． A．5° 5° 4° B．5° 5° 4.5° C．2.8° 5° 4° D．2.8° 5° 4.5° 2．已知甲、乙两组数据的平均数都是5，甲组数据的方差＝，乙组数据的方差＝，那么下列说法正确的是( )． (A)甲组