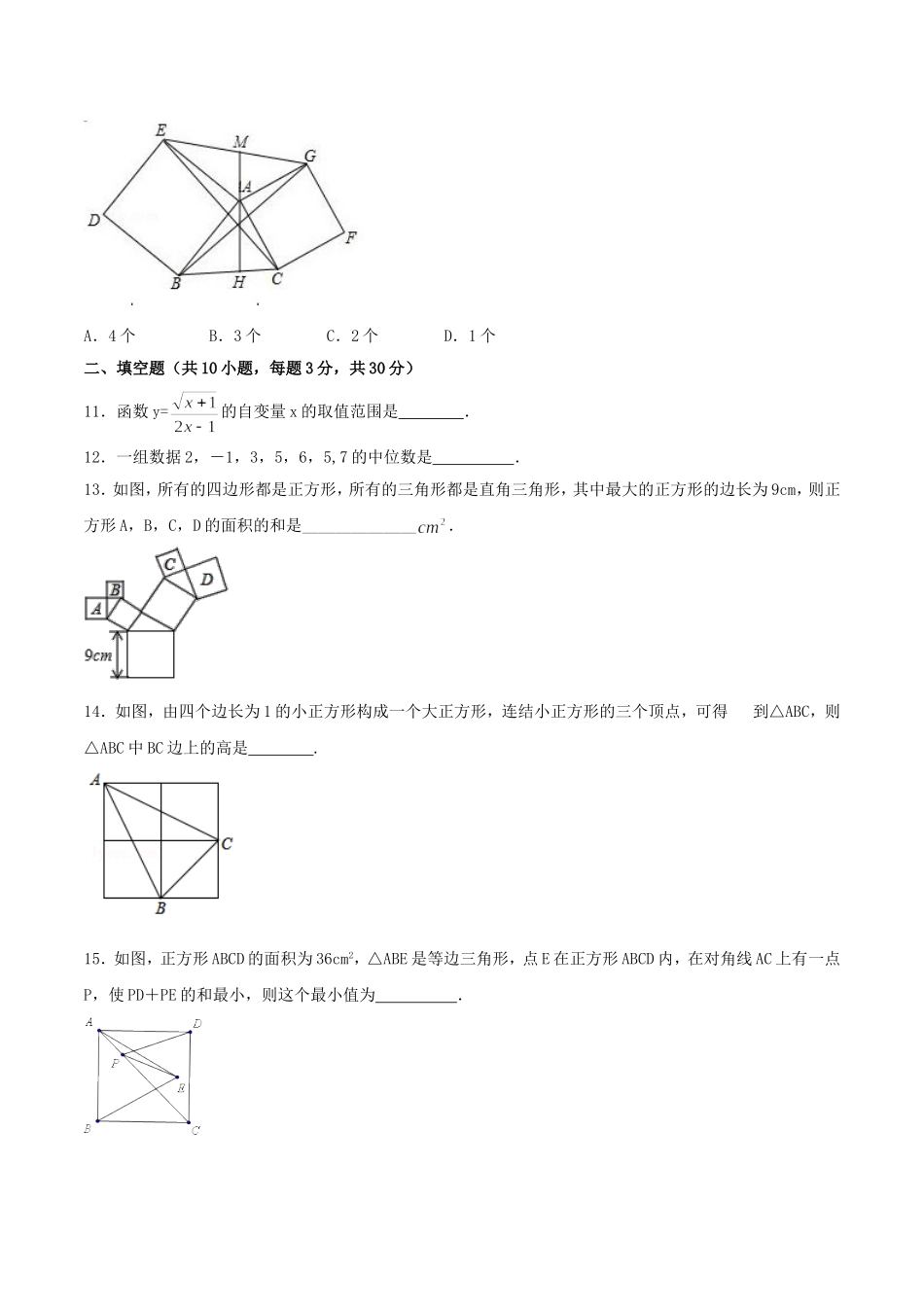
《八年下数学期末》测试卷(二)(A卷)(测试时间:90分钟满分:120分)一.选择题(共10小题,每题3分,共30分)1.若式子有意义,则x的取值范围为().A.B.C.或D.且2.下列运算正确的是()A.5B.[来源:学#科#网]C.(-a-b)2=a2-2ab+b2D.3.某商场对上月笔袋销售的情况进行统计如下表所示:颜色白色黄色蓝色紫色红色数量(个)56128520210160经理决定本月进笔袋时多进一些蓝色的,经理的这一决定应用了哪个统计知识()A.平均数B.方差C.中位数D.众数4.将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为()A.3cmB.6cmC.3cmD.6cm5.已知下列命题:①若a>0,b>0,则a+b>0;②若a2≠b2,则a≠b③角平分线上的点到角两边的距离相等;④平行四边形的对角线互相平分⑤直角三角形斜边上的中线等于斜边的一半.其中原命题与逆命题均为真命题的是()A、①③④B、①②④C、③④⑤D、②③⑤6.下列图形中,∠2>∠1的是()A.B.C.则D.7.表示一次函数与正比例函数(m、n是常数且)图象是()8.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为()A.x≥B.x≤3C.x≤D.x≥39.如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解是()A.B.C.D.10.在锐角三角形ABC中,AH是BC边上的高,分别以AB、AC为一边,向外作正方形ABDE和ACFG,连接CE、BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE②BG⊥CE③AM是△AEG的中线④∠EAM=∠ABC,其中正确结论的个数是()A.4个B.3个C.2个D.1个二、填空题(共10小题,每题3分,共30分)11.函数y=的自变量x的取值范围是.12.一组数据2,-1,3,5,6,5,7的中位数是.[来源:学科网]13.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm,则正方形A,B,C,D的面积的和是______________.[来源:学科网]14.如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是.15.如图,正方形ABCD的面积为36cm2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为.16.如图,矩形ABCD中,AD=,F是DA延长线上一点,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F=20°,则AB=.17.如...