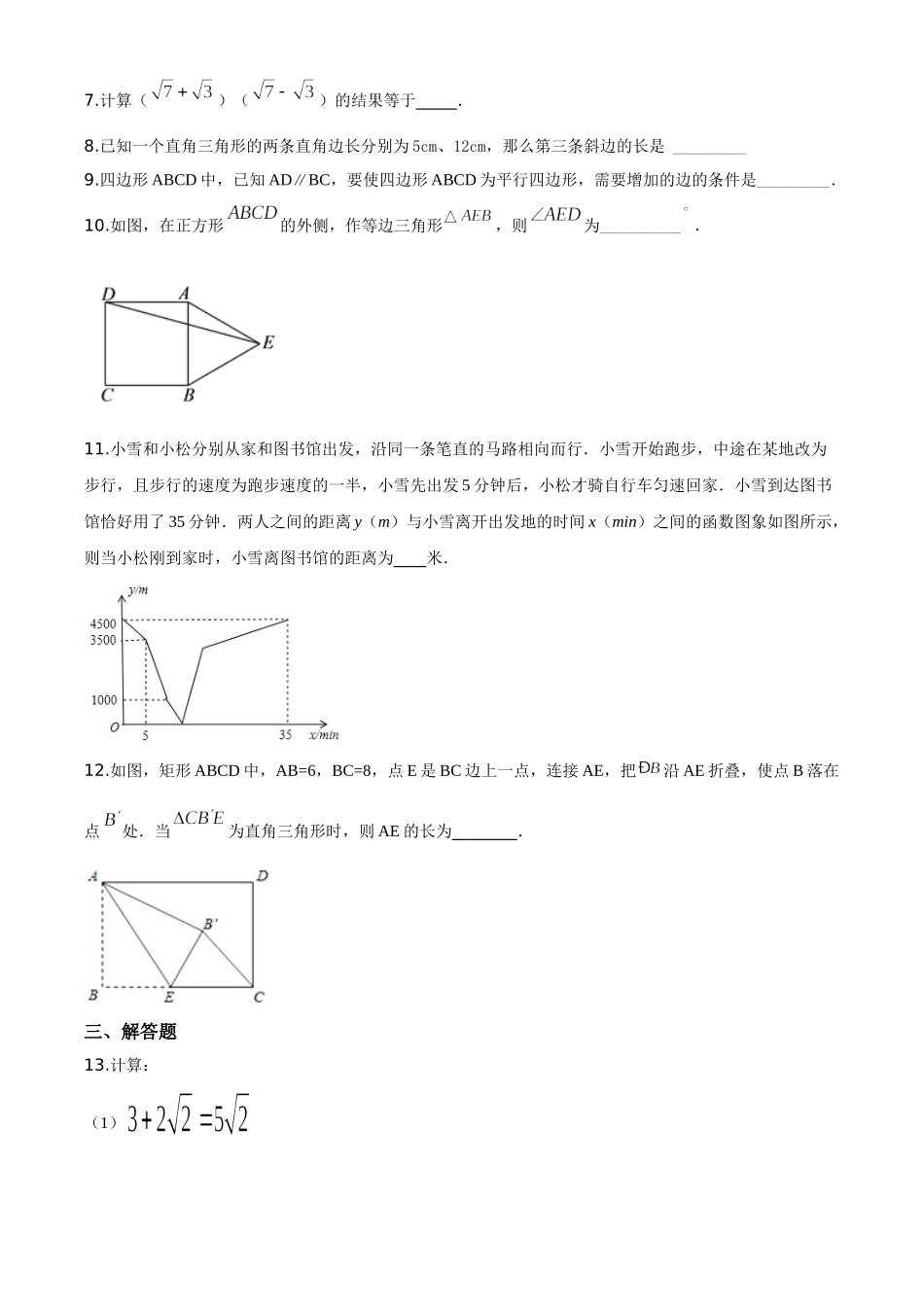
下学期期中考试八年级数学试卷一、选择题1.式子有意义,则实数a的取值范围是()A.a≥-1B.a≠2C.a≥-1且a≠2D.a>22.三角形的三边长a、b、c满足a2+b2-c2=0,则此三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形3.下列计算正确的是()A.B.C.D.4.四边形的对角线与相交于点,下列四组条件中,一定能判定四边形为平行四边形的是()A.B.,C.,D.5.在正比例函数中,函数的值随值的增大而增大,则点在()A.第一象限B.第二象限C.第三象限D.第四象限6.如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为()A.B.C.D.二、耐心填一填,一锤定音!7.计算()()的结果等于_____.8.已知一个直角三角形的两条直角边长分别为5cm、12cm,那么第三条斜边的长是_________9.四边形ABCD中,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的边的条件是_________.10.如图,在正方形的外侧,作等边三角形,则为__________.11.小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.12.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把沿AE折叠,使点B落在点处.当为直角三角形时,则AE的长为________.三、解答题13.计算:(1)(2)14.如图,正方形网格中的每个小正方形边长都是l,每个小格的顶点叫做格点.以格点为顶点分别按下列要求画图:(1)画出一个平行四边形,使其面积为6;(2)画出一个菱形,使其面积为4.(3)画出一个正方形,使其面积为5.15.已知y+1与x+3成正比例,且当x=5时,y=3.(1)求y与x之间的函数关系式;(2)当y=1时,求x的值.16.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别为AO,CO的中点,求证:BF∥DE17.如图,四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:四边形AECF是平行四边形.18.如图,四边形是平行四边形,,垂足分别为,且.(1)求证:四边形是菱形;(2)连接并延长,交的延长线于点,若,求的长.19.如图,直线的解析式为:,且与轴交于点,直线经过点,,直线,交于点.(1)求直线的解析表达式;...