八年级数学下册 第18章 平行四边形单元综合检测（三）（新版）新人教版.doc

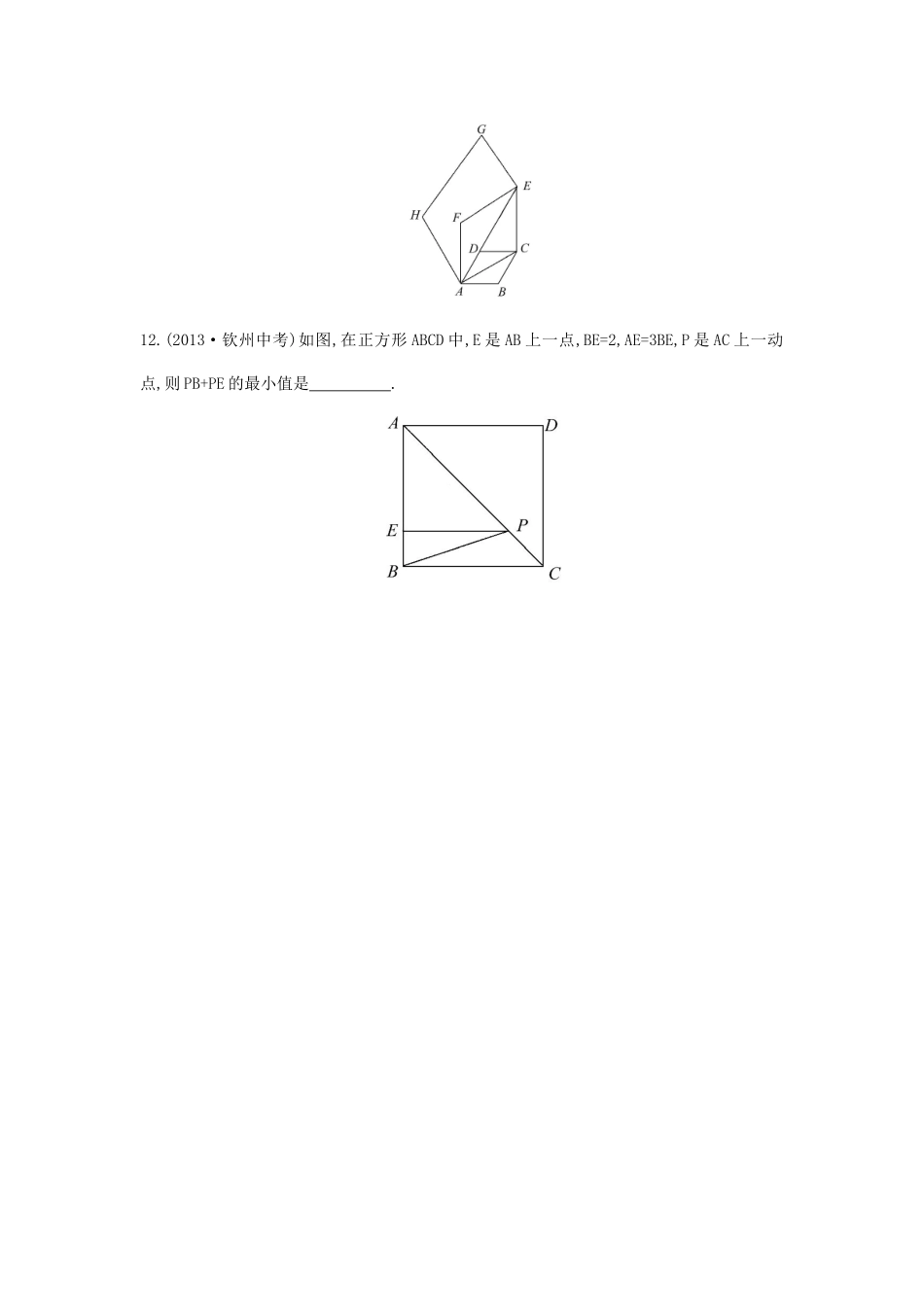
第18章 平行四边形单元综合检测（三） 一、选择题(每小题4分,共28分) 1.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是 (　　) 2.如图,已知菱形ABCD的对角线AC,BD的长分别是6cm,8cm,AE⊥BC于点E,则AE的长是(　　) A.5cm 　　　 B.2cm C.cm 　　　 D.cm 3.如图,在平行四边形ABCD中,DE是∠ADC的平分线,F是AB的中点,AB=6,AD=4,则AE∶EF∶BE为(　　) A.4∶1∶2 B.4∶1∶3 C.3∶1∶2 D.5∶1∶2 4.(2013·邵阳中考)如图所示,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连接BE交CD于点O,连接AO,下列结论不正确的是(　　) A.△AOB≌△BOC B.△BOC≌△EOD C.△AOD≌△EOD D.△AOD≌△BOC 5.如图,过矩形ABCD的四个顶点作对角线AC,BD的平行线,分别相交于E,F,G,H四点,则四边形EFGH为(　　) A.平行四边形 B.矩形 C.菱形 D.正方形 6.(2013·威海中考)如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是(　　) A.BC=AC 　　 B.CF⊥BF C.BD=DF 　　 D.AC=BF 7.如图,△ABC中,AB=AC,点D,E分别是边AB,AC的中点,点G,F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为(　　) A.3cm 　　 B.4cm C.2cm 　　 D.2cm 二、填空题(每小题5分,共25分) 8.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为　　　　. 9.(2013·厦门中考)如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF=　　　　厘米. 10.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是　　　　. 11.(2013·牡丹江中考)如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是　　　　. 12.(2013·钦州中考)如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是　　　　　. 三、解答题(共47分) 13.(10分)(2013·大连中考)如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且AE=CF. 求证:BE=DF. 14.(12分)(2013·晋江中考)如图,BD是菱形ABCD的对角线,点E,F分别在边CD,DA上,且CE=AF.求证:BE=BF. 15.(12分)(2013·铁岭中考)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE. (1)求证:四边形AEBD是矩形. (2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由. 16.(13分)(2013·济宁中考)如图1,在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE. (1)求证:AF=BE. (2)如图2,在正方形ABCD中,M,N,P,Q分别是边AB,BC,CD,DA上的点,且MP⊥NQ,判断MP与NQ是否相等?并说明理由. 答案解析 1.【解析】选C.A项,根据两直线平行内错角相等可得到,故正确;B项,根据对顶角相等可得到,故正确;C项,根据两直线平行内错角相等可得到∠1=∠ACB,∠2为一外角,所以不相等,故不正确;D项,根据平行四边形对角相等可得到,故正确. 2.【解析】选D.由于菱形ABCD的对角线AC,BD的长分别是6cm,8cm,所以菱形边长为=5,所以×6×8=5AE,解得AE=. 3.【解析】选A.∵四边形ABCD是平行四边形, ∴∠CDE=∠DEA. ∵DE是∠ADC的平分线,∴∠CDE=∠ADE, ∴∠DEA=∠ADE,∴AE=AD=4. ∵F是AB的中点,∴AF=AB=3. ∴EF=AE-AF=1,BE=AB-AE=2, ∴AE∶EF∶BE=4∶1∶2. 4.【解析】选A.∵AD=DE,DO∥AB, ∴OD为△ABE的中位线,∴OD=OC, ∵在△AOD和△EOD中, ∴△AOD≌△EOD; ∵在△AOD和△BOC中, ∴△AOD≌△BOC; ∵△AOD≌△EOD,∴△BOC≌△EOD; 故B,C,D选项均正确. 5.【解析】选C.∵EH∥BD,FG∥BD,∴EH∥FG,又EF∥AC,∴四边形AEFC是平行四边形,∴EF=AC,同理GH=AC,EH=BD,FG=BD.∵在矩形ABCD中,AC=BD, ∴EF=FG=GH=EH,∴四边形EFGH是菱形. 6.【解析】选D.∵EF垂直平分BC, ∴BE=EC,BF=CF, ∵BF=BE,∴BE=EC=CF=BF, ∴四边形BECF是菱形. 当BC=AC时,∵∠ACB=90°,则∠A=45°. ∵∠A=45°,∠ACB=90°,∴∠EBC=45°. ∴∠EBF=2∠EBC=2×45°=90°, ∴菱形BECF是正方形. 当CF⊥BF时,利用正方形的判定定理得出,菱形BECF是正方形; 当BD=DF时,利用正方形的判定得出,菱形BECF是正方形; 当AC=BF时,无法得出菱形BECF是正方形,故选项D符合题意. 7.【解析】选D.∵点D,E分别是边AB,AC的中点, ∴DE=BC, ∵DE=2cm,∴BC=4cm, ∵AB=AC,四边形DEFG是正方形. ∴△BDG≌△CEF,∴BG=CF=1cm, ∴EC=,∴AC=2cm. 8.【解析】设CE与AD相交于点F. ∵在平行四边形ABCD中,过点C的直线CE⊥AB, ∴∠E=90°, ∵∠EAD=53°, ∴∠EFA=90°-53°=37°,∴∠DFC=37°. ∵四边形ABCD是平行四边形, ∴AD∥BC,∴∠BCE=∠DFC=37°. 答案:37° 9.【解析】∵▱ABCD的对角线AC,BD相交于点O,AC+BD=24厘米,∴OA+OB=12厘米. ∵△OAB的周长是18厘米,∴AB=6厘米. ∵点E,F分别是线段AO,BO的中点, ∴EF=3厘米. 答案:3 10.【解析】∵CE∥BD,DE∥AC, ∴四边形CODE是平行四边形. ∵四边形ABCD是矩形, ∴AC=BD=4,OA=OC=OB=OD, ∴OD=OC=AC=2, ∴四边形CODE是菱形, ∴四边形CODE的周长为4OC=4×2=8. 答案:8 11.【解析】连接DB, ∵四边形ABCD是菱形, ∴AD=AB,AC⊥DB, ∵∠DAB=60°, ∴△ADB是等边三角形, ∴DB=AD=1,∴BM=, ∴AM=,∴AC=, 同理可得AE=AC=()2, AG=AE=3=()3, 按此规律所作的第n个菱形的边长为()n-1. 答案:()n-1 12.【解析】如图,连接DE,交AC于点P,连接BP, 则此时PB+PE的值最小. ∵四边形ABCD是正方形, ∴B,D关于AC对称, ∴PB=PD, ∴PB+PE=PD+PE=DE. ∵BE=2,AE=3BE, ∴AE=6,AB=8, ∴DE==10, 故PB+PE的最小值是10. 答案:10 13.【证明】∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC, ∵AE=CF,∴DE=BF,DE∥BF, ∴四边形DEBF是平行四边形, ∴BE=DF. 14.【证明】∵四边形ABCD是菱形, ∴AB=BC,∠A=∠C. 在△ABF和△CBE中, ∴△ABF≌△CBE(SAS), ∴BF=BE. 15.【解析】(1)∵点O为AB的中点,连接DO并延长到点E,使OE=OD, ∴四边形AEBD是平行四边形, ∵AB=AC,AD是△ABC的角平分线, ∴AD⊥BC,∴∠ADB=90°, ∴平行四边形AEBD是矩形.即四边形AEBD是矩形. (2)当∠BAC=90°时,矩形AEBD是正方形.理由: ∵∠BAC=90°,AB=AC,AD是△ABC的角平分线, ∴AD=BD=CD, ∵由(1)得四边形AEBD是矩形, ∴矩形AEBD是正方形. 16.【解析】(1)在正方形ABCD中,AB=AD,∠BAE=∠D=90°, ∴∠DAF+∠BAF=90°, ∵AF⊥BE,∴∠ABE+∠BAF=90°, ∴∠ABE=∠DAF, ∵在△ABE和△DAF中, ∴△ABE≌△DAF(ASA),∴AF=BE. (2)MP与NQ相等. 理由如下:如图,过点A作AF∥MP交CD于点F,过点B作BE∥NQ交AD于点E, 则与(1)的情况完全相同.而MP=AF,NQ=BE, ∴MP=NQ.