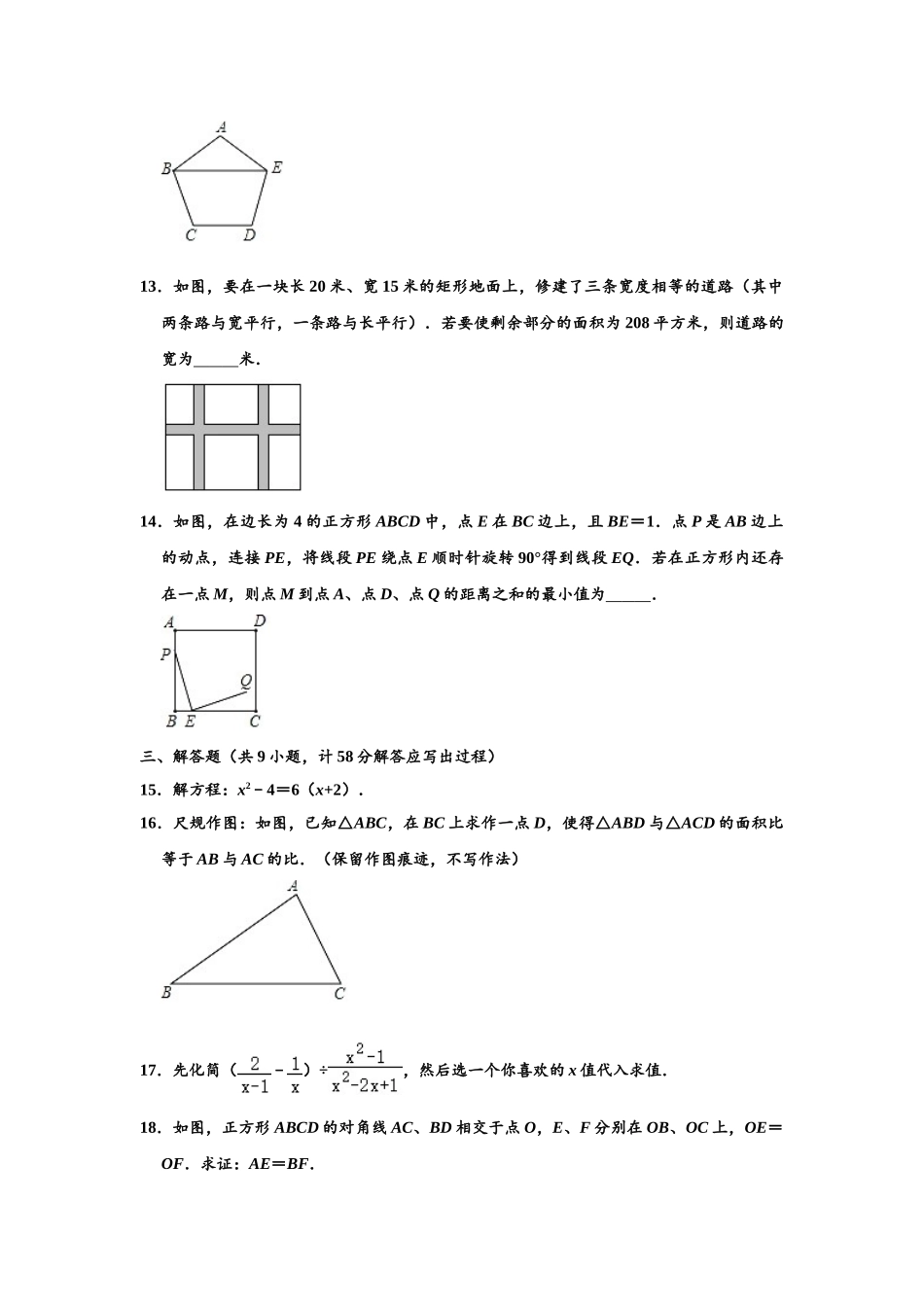
八年级第二学期期末数学试卷一、选择题1.下列方程中,是一元二次方程是()A.2x+3y=4B.x2=0C.x2﹣2x+1>0D.=x+22.下列图形既是中心对称图形,又是轴对称图形的是()A.直角三角形B.等腰三角形C.平行四边形D.菱形3.下列由左到右变形,属于因式分解的是()A.x+1=x(1+)B.(x+2)(x﹣2)=x2﹣4C.x2﹣x=x(x﹣1)D.x2﹣2x+1=x(x﹣2)+14.如图,在Rt△ABC中,CD、CE分别是斜边上的中线、高线.若∠A=25°,则∠DCE的大小为()A.50°B.40°C.30°D.25°5.能使分式的值为零的x的值是()A.x=﹣1B.x=1C.x1=1,x2=﹣1D.x1=0,x2=16.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线互相垂直的四边形D.对角线相等的四边形7.不等式组的解集是()A.﹣2<x≤2B.x<﹣2C.x≥2D.无解8.如图,在矩形ABCD中,AB=4,AD=8,点E、点F分别在AD、BC上.若四边形EBFD为菱形,则EF的长为()A.2B.4C.2D.59.在平面直角坐标系中,将函数y=2x的图象向上平移m(m>0)个单位长度,使其与直线y=﹣x+4的交点位于第二象限,则m的取值范围为()A.0<m<2B.2<m<4C.m≥4D.m>410.如图,在菱形ABCD中,AB=5,对角线BD=8.点P、点Q分别是AB、BD上动点,则AQ+PQ的最小值为()A.B.C.5D.二、填空题(共4小题,每小题3分,计12分)11.因式分解:x3y﹣4xy3=.12.如图,已知正五边形ABCDE,连接BE,则∠CBE的大小为°.13.如图,要在一块长20米、宽15米的矩形地面上,修建了三条宽度相等的道路(其中两条路与宽平行,一条路与长平行).若要使剩余部分的面积为208平方米,则道路的宽为米.14.如图,在边长为4的正方形ABCD中,点E在BC边上,且BE=1.点P是AB边上的动点,连接PE,将线段PE绕点E顺时针旋转90°得到线段EQ.若在正方形内还存在一点M,则点M到点A、点D、点Q的距离之和的最小值为.三、解答题(共9小题,计58分解答应写出过程)15.解方程:x2﹣4=6(x+2).16.尺规作图:如图,已知△ABC,在BC上求作一点D,使得△ABD与△ACD的面积比等于AB与AC的比.(保留作图痕迹,不写作法)17.先化简(﹣)÷,然后选一个你喜欢的x值代入求值.18.如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.19.已知关于x的一元二次方程x2﹣2mx+(m2+m)=0有两个实数根.(1)求m的取值范围;(2)如果方程的两个实数根...