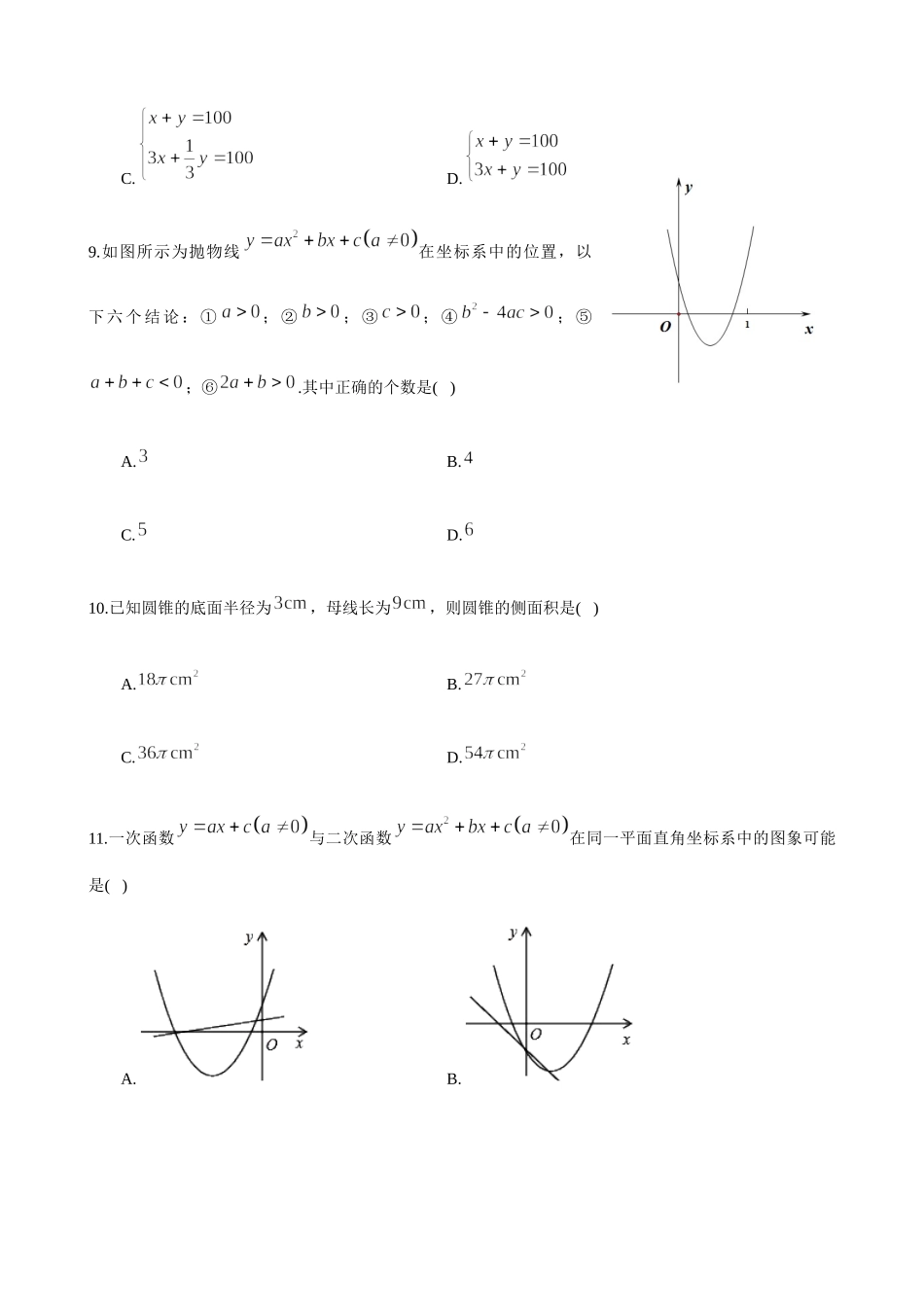
第二学期期末考试卷初二数学总分:120分时量:120分钟一、选择题(本大题共12小题,共36分)1.下列各式运算结果是负数的是()A.B.C.D.2.为庆祝中华人民中国成立周年,我国于年月1日在北京天安门广场举行大型阅兵仪式,在此次活动中,共有个徒步方队,个装备方队,空中梯队个,约名官兵通过天安门广场接受党和人民的检阅.将数字用科学计数法表示为()A.B.C.D.3.下列运算中正确的是()A.B.C.D.4.如图,在三角形中,,三角形的高线,交于点,则的度数()A.B.C.D.5.如图,,交于点,,则等于()A.B.C.D.6.一个样本的方差是,若中位数是,那么它的平均数是()A.等于B.不等于C.大于D.小于7.下列命题是真命题的是()A.一组对边平行另一组对边相等的四边形是平行四边形B.一组邻边相等的平行四边形是菱形C.对角线相等的四边形是矩形D.对角线垂直的四边形是菱形8.我国古代数学名著《孙子算经》中记载了一道题,大意是:求匹马恰好拉了片瓦,已知1匹大马能拉片瓦,匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,那么可列方程组为()A.B.C.D.9.如图所示为抛物线在坐标系中的位置,以下六个结论:①;②;③;④;⑤;⑥.其中正确的个数是()A.B.C.D.10.已知圆锥的底面半径为,母线长为,则圆锥的侧面积是()A.B.C.D.11.一次函数与二次函数在同一平面直角坐标系中的图象可能是()A.B.C.D.12.如图,抛物线的图象与坐标轴交于点,,,顶点为,以为直径画半圆交负半轴交于点,圆心为,是半圆上的一动点,连接.①点在的内部;②的长为;③若与重合,则;④在的运动过程中,若,则;⑤是的中点,当沿半圆从点运动至点时,点运动的路径长是.则正确的选项为()A.①②④B.②③④C.②③⑤D.③④⑤二、填空题(本大题共6小题,每小题3分,共18分)13.分解因式的结果是________.14.若一元二次方程有两个实数根,,则的值是________.15.正六边形的外接圆的半径与内切圆的半径之比为________.16.如图,点,,都在上,若,则的度数是________度.17.将二次函数的图象先向右平移1个单位,再向上平移个单位,平移后的得到图像函数表达式是________.18.抛物线与直线交于、两点,且,则________.三、解答题(本大题共8个小题)19.计算:(1);(2)解一元二次方程.20.先化简代数式:,再从,,这三个数中,选择一个恰当的数作为的值,代入求值.21.某中学对本校学生每天完成作业所用时间的情况进行了抽样调查.随机调查了九年级部分学生每天完成作业所用的时间,并根据统计结果制...