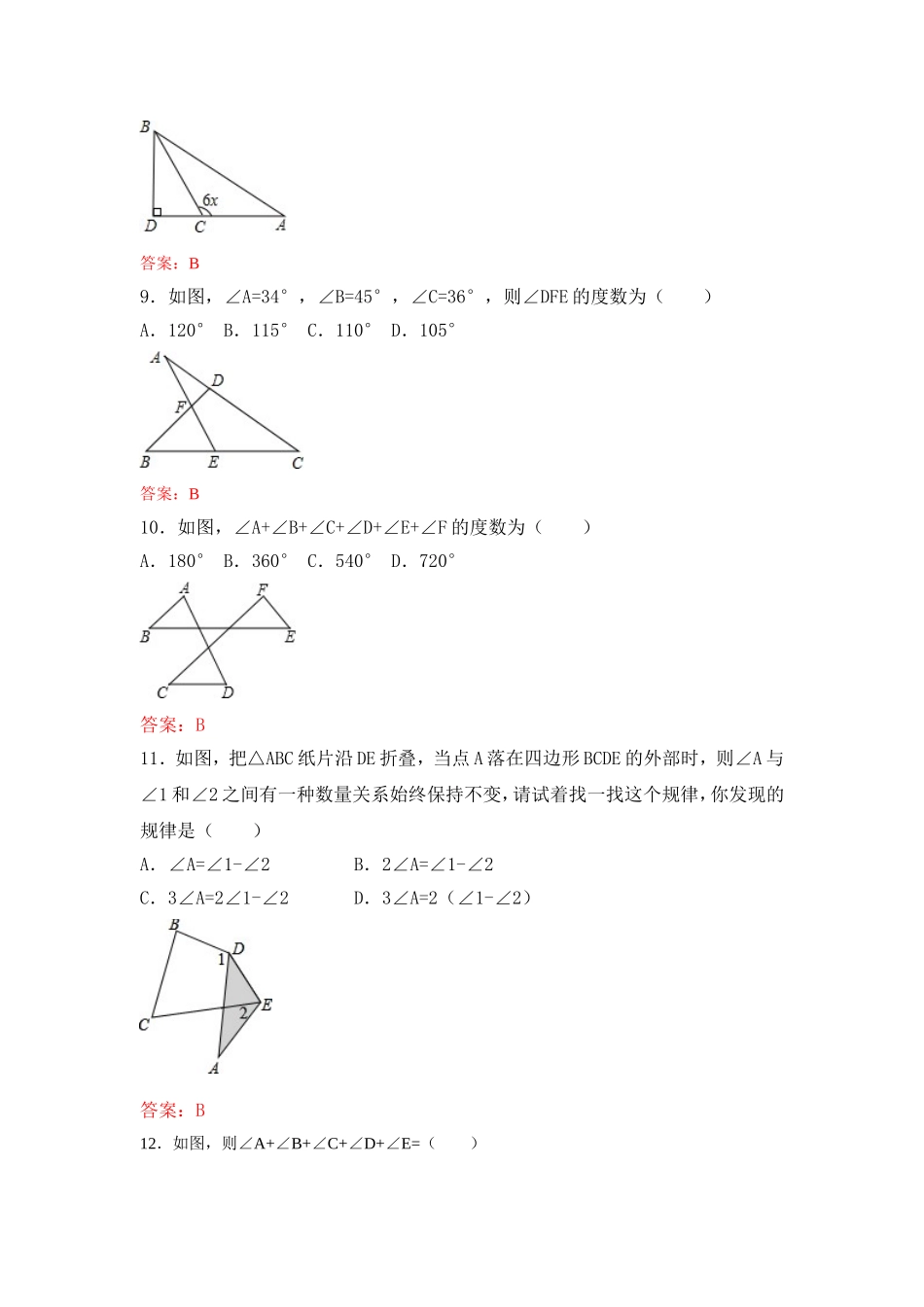
11.2.2三角形的外角基础知识一、选择题1.(2013•襄阳)如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于()A.60°B.70°C.80°D.90°答案:C2.(2013•湘西州)如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是()A.15°B.25°C.30°D.10°答案:A3.设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ中()A.有两个锐角、一个钝角B.有两个钝角、一个锐角C.至少有两个钝角D.三个都可能是锐角答案:C4.(2012江苏省南通市)如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2等于()A.360°B.250°C.180°D.140°答案:BACB125.已知△ABC,(1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-∠A.上述说法正确的个数是()A.0个B.1个C.2个D.3个答案:C6.(2012•漳州)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是()A.45°B.60°C.75°D.90°答案:C7.如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是()A.61°B.60°C.37°D.39°答案:C8.如图,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是()A.10°B.20°C.30°D.40°答案:B9.如图,∠A=34°,∠B=45°,∠C=36°,则∠DFE的度数为()A.120°B.115°C.110°D.105°答案:B10.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为()A.180°B.360°C.540°D.720°答案:B11.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是()A.∠A=∠1-∠2B.2∠A=∠1-∠2C.3∠A=2∠1-∠2D.3∠A=2(∠1-∠2)答案:B12.如图,则∠A+∠B+∠C+∠D+∠E=()A.90B.180C.200D.360答案:B13.如图,BD、CD分别平分∠ABC和∠ACE,∠A=40°,则∠D的度数是()A.20°B.30°C.40°D.60°答案:A14.如图,等边三角形ABC,P为BC上一点,且∠1=∠2,则∠3为()A.50°B.60°C.75°D.无法确定答案:B二、填空题2.如图,已知ΔABC中,∠ABC和外角∠ACE的平分线相交于点D,若∠D=400,则∠BAC的度数为.1.如图,BP、CP是任意△ABC中∠B、∠C的角平分线,可知∠BPC=90°+∠A,把图...