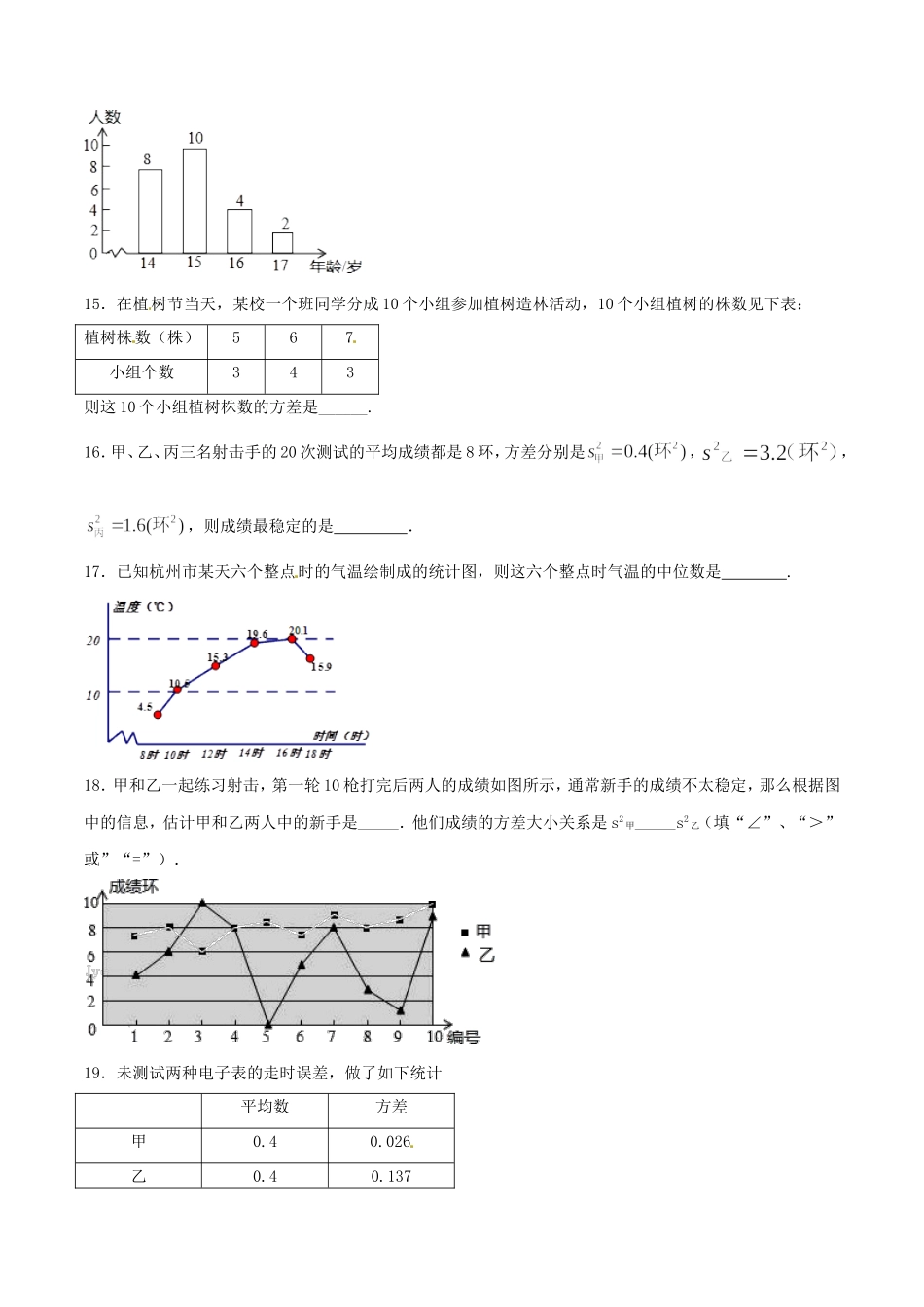
《第二十章数据的分析》测试卷(B卷)(测试时间:90分钟满分:120分)一、选择题(共10小题,每题3分,共30分)1.某班第一小组6名女生在测仰卧起坐时,记录下她们的成绩(单位:个/分):45,48,46,50,50,49.这组数据的平均数是()A.49B.48C.47D.462.有一组数据如下:3,6,5,2,3,4,3,6.那么这组数据的中位数是()A.3或4B.4C.3D.3.53.A居民区的月底统计用电情况,其中3户用电45度,5户用电50度,6户用电42度,则平均用电为()A.41度B.42度C.45.5度D.46度4.某小组10个女生做仰卧起坐,仰卧起坐次数的测试数据如下表,则这组数据的众数和中位数分别是()次数3538404142人数11332A.38.8和40B.40和40C.40和40.5D.38.8和40.55.数据70、71、72、73、74的方差是()A.B.2C.D.6.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这七名同学成绩的()A.众数B.平均数C.中位数D.方差7.甲、乙两人在相同的条件下各射靶10次,射击成绩的平均数都是8环,甲射击成绩的方差是1.2,乙射击成绩的方差是1.8.下列说法中不一定正确的是()[来源:学科网]A.甲、乙射击成绩的众数相同B.甲射击成绩比乙稳定C.乙射击成绩的波动比甲较大D.甲、乙射中的总环数相同8.一次体检中,某班学生视力检查的结果如图所示,从图中看出全班视力数据的众数是()(A)55%(B)24%(C)1.0(D)1.0以上9.如图是某射击选手5次设计成绩的折线图,根据图示信息,这5次成绩的众数、中位数分别是()A.7、8B.7、9C.8、9D.8、1010.李大伯有一片果林,共80棵果树,某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得果子,质量分别为(单位:kg):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23,以此计算,李大伯收获的这批果子的单个质量和总质量分别约为()A.0.25kg,200kgB.2.5kg,100kgC.0.25kg,100kgD.2.5kg,200kg二.填空题(共10小题,每题3分,共30分)11.某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如下表:时间(单位:小时)43210人数24211则这10名学生周末利用网络进行学习的平均时间是小时。12.一组数据1,3,2,5,x的平均数为3,那么这组数据的中位数是__________.13.一组数据1,3,2,5,2,a的唯一众数...