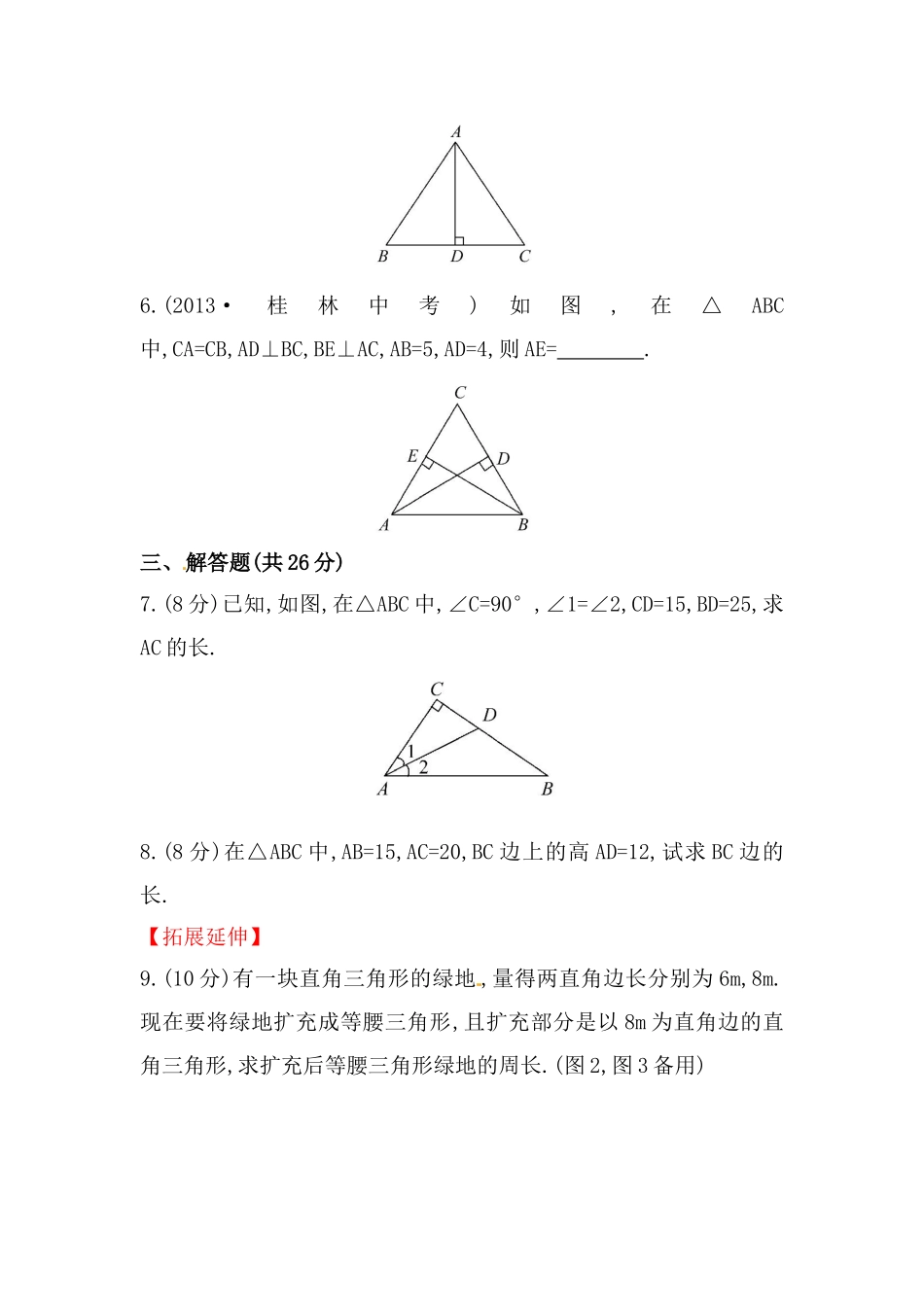
勾股定理一、选择题(每小题4分,共12分)1.(2013·黔西南州中考)一直角三角形的两边长分别为3和4.则第三边的长为()A.5B.C.D.5或2.如图,有一块直角三角形纸板ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且点C落到点E处,则CD等于()A.2cmB.3cmC.4cmD.5cm3.(2013·资阳中考)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是()A.48B.60C.76D.80[来源:学科网ZXXK]二、填空题(每小题4分,共12分)4.(2013·莆田中考)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为2,5,1,2.则最大的正方形E的面积是.5.如图,等腰△ABC中,AB=AC,AD是底边上的高,若AB=5cm,BC=6cm,则AD=cm.[来源:学科网ZXXK]6.(2013·桂林中考)如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE=.[来源:学科网ZXXK]三、解答题(共26分)[来源:学§科§网Z§X§X§K]7.(8分)已知,如图,在△ABC中,∠C=90°,∠1=∠2,CD=15,BD=25,求AC的长.8.(8分)在△ABC中,AB=15,AC=20,BC边上的高AD=12,试求BC边的长.【拓展延伸】9.(10分)有一块直角三角形的绿地,量得两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.(图2,图3备用)[来源:学&科&网Z&X&X&K]答案解析1.【解析】选D.(1)当两边均为直角边时,由勾股定理得,第三边长为5;(2)当4为斜边时,由勾股定理得,第三边长为,故选D.2.【解析】选B.由题意可知,△ACD和△AED关于直线AD对称,因而△ACD≌△AED.所以AE=AC=6cm,CD=ED,ED⊥AB,设CD=ED=xcm,则在Rt△ABC中,由勾股定理可得AB2=AC2+BC2=62+82=100,得AB=10cm,在Rt△BDE中,有x2+(10-6)2=(8-x)2.解得x=3.【归纳整合】运用勾股定理解决折叠问题,往往融方程与几何图形于一体,具有较强的综合性.解决与折叠有关的问题时,要寻找出折叠前后的不变量(即相等的线段、相等的角),同时要注意方程思想的应用.3.【解析】选C. ∠AEB=90°,AE=6,BE=8,∴在Rt△ABE中,AB2=AE2+BE2=100,∴S阴影部分=S正方形ABCD-S△ABE=AB2-×AE×BE=100-×6×8=76.4.【解析】如图,根据勾股定理的几何意义,可得A,B的面积和为S1,C,D的面积和为S2,S1+S2=S3,即S3=2+5+1+2=10.答案:105.【解析】根据等腰三角形的三线合一可得:BD=BC=×6=3(cm),在直角三角形ABD中,由勾股定理得:AB2=BD2+AD2,所以AD===4(cm).答案:46.【解析】在Rt△ADB中,根据勾股定理,得DB===3. AD⊥BC,BE...