11.2 与三角形有关的角 同步练习及答案.doc

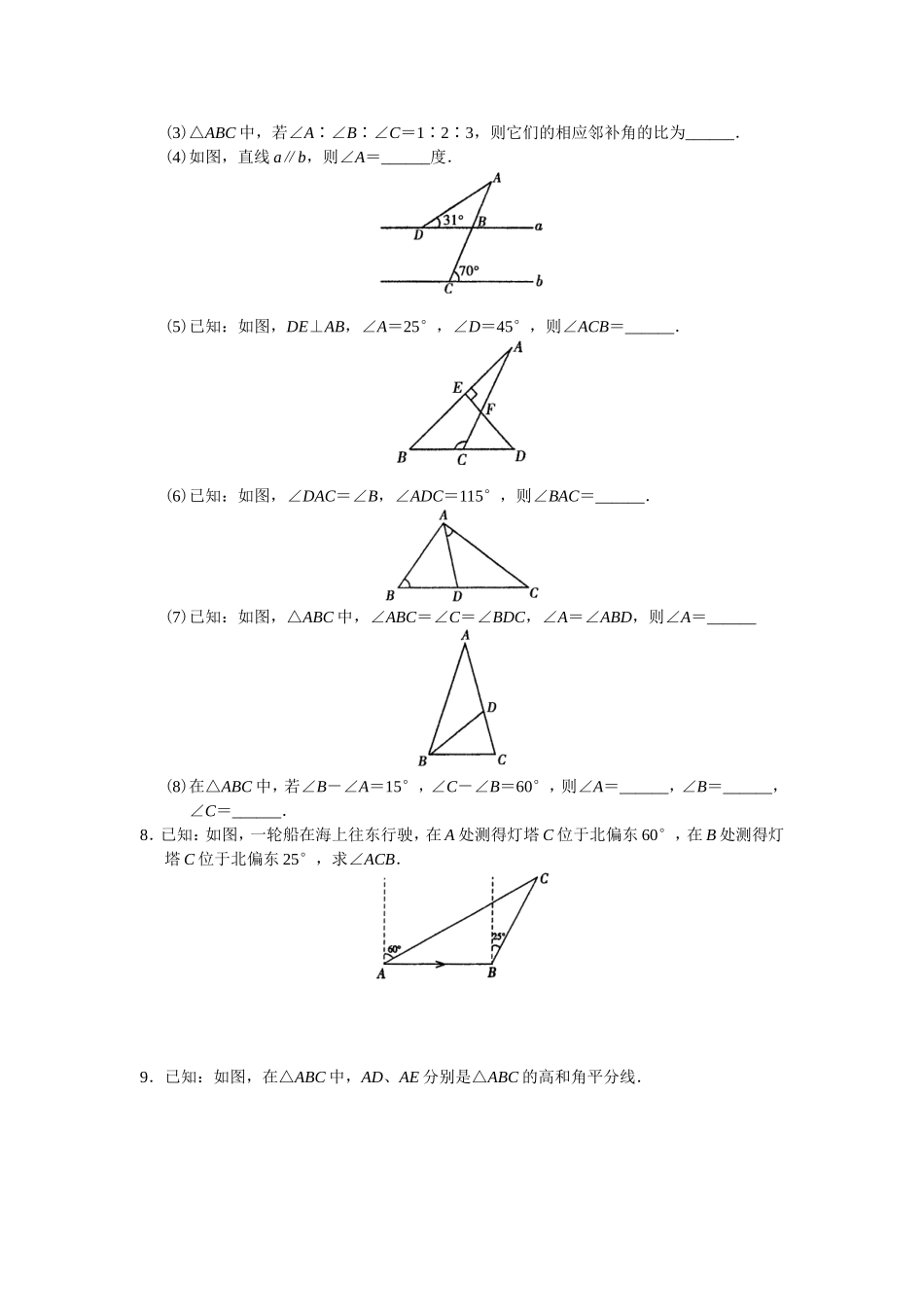
第11章《三角形》 同步练习 （§11.2 与三角形有关的角） 班级 学号 姓名 得分 1．填空： (1)三角形的内角和性质是____________________________________________________. (2)三角形的内角和性质是利用平行线的______与______的定义，通过推理得到的．它的推理过程如下： 已知：△ABC， 求证：∠BAC＋∠ABC＋∠ACB＝______． 证明：过A点作______∥______， 则∠EAB＝______，∠FAC＝______． (___________，___________) ∵∠EAF是平角， ∴∠EAB＋______＋______＝180°．( ) ∴∠ABC＋∠BAC＋∠ACB＝∠EAB＋∠______＋∠______．( ) 即∠ABC＋∠BAC＋∠ACB＝______． 2．填空： (1)三角形的一边与_________________________________________叫做三角形的外角． 因此，三角形的任意一个外角与和它相邻的三角形的一个内角互为______． (2)利用“三角形内角和”性质，可以得到三角形的外角性质? 如图，∵∠ACD是△ABC的外角， ∴∠ACD与∠ACB互为______， 即∠ACD＝180°－∠ACB．① 又∵∠A＋∠B＋∠ACB＝______， ∴∠A＋∠B＝______．② 由①、②，得∠ACD＝______＋______． ∴∠ACD＞∠A，∠ACD＞∠B 由上述(2)的说理，可以得到三角形外角的性质如下： 三角形的一个外角等于____________________________________________________. 三角形的一个外角大于____________________________________________________. 3．(1)已知：如图，∠1、∠2、∠3分别是△ABC的外角， 求：∠1＋∠2＋∠3． (2)结论：三角形的外角和等于______． 4．已知：如图，BE与CF相交于A点，试确定∠B＋∠C与∠E＋∠F之间的大小关系，并说明你的理由． 5．已知：如图，CE⊥AB于E，AD⊥BC于D，∠A＝30°，求∠C的度数． 6．依据题设，写出结论，想一想，为什么? 已知：如图，△ABC中，∠ACB＝90°，则： (1)∠A＋∠B＝______．即∠A与∠B互为______； (2)若作CD⊥AB于点D，可得∠BCD＝∠______，∠ACD＝∠______． 7．填空： (1)△ABC中，若∠A＋∠C＝2∠B，则∠B＝______． (2)△ABC中，若∠A∶∠B∶∠C＝2∶3∶5，则∠A＝______，∠B＝______，∠C＝______． (3)△ABC中，若∠A∶∠B∶∠C＝1∶2∶3，则它们的相应邻补角的比为______． (4)如图，直线a∥b，则∠A＝______度． (5)已知：如图，DE⊥AB，∠A＝25°，∠D＝45°，则∠ACB＝______． (6)已知：如图，∠DAC＝∠B，∠ADC＝115°，则∠BAC＝______． (7)已知：如图，△ABC中，∠ABC＝∠C＝∠BDC，∠A＝∠ABD，则∠A＝______ (8)在△ABC中，若∠B－∠A＝15°，∠C－∠B＝60°，则∠A＝______，∠B＝______，∠C＝______． 8．已知：如图，一轮船在海上往东行驶，在A处测得灯塔C位于北偏东60°，在B处测得灯塔C位于北偏东25°，求∠ACB． 9．已知：如图，在△ABC中，AD、AE分别是△ABC的高和角平分线． (1)若∠B＝30°，∠C＝50°，求∠DAE的度数． (2)试问∠DAE与∠C－∠B有怎样的数量关系?说明理由． 10．已知：如图，O是△ABC内一点，且OB、OC分别平分∠ABC、∠ACB． (1)若∠A＝46°，求∠BOC； (2)若∠A＝n°，求∠BOC； (3)若∠BOC＝148°，利用第(2)题的结论求∠A． 11．已知：如图，O是△ABC的内角∠ABC和外角∠ACE的平分线的交点． (1)若∠A＝46°，求∠BOC； (2)若∠A＝n°，用n的代数式表示∠BOC的度数． 12．类比第10、11题，若O是△ABC外一点，OB、OC分别平分△ABC的外角∠CBE、∠BCF，若∠A＝n°，画出图形并用n的代数表示∠BOC． 13．如图，点M是△ABC两个内角平分线的交点，点N是△ABC两个外角平分线的交点，如果∠CMB；∠CNB＝3∶2 求∠CAB的度数． 14．如图，已知线段AD、BC相交于点Q，DM平分∠ADC，BM平分∠ABC，且∠A＝27°，∠M＝33°，求∠C的度数． 参考答案 1．(1)三角形的内角和等于180°，(2)性质、平角，说理过程(略) 2．略． 3．∠1＋∠2＋∠3＝360°，360°． 4．∠B＋∠C＝∠E＋∠F．(此图中的结论为常用结论) 5．30° 6．(1)90°，余角，(2)∠A，∠B 7．(1)60°．(2)36°，54°，90°．(3)5∶4∶3．(4)39°．(5)110°． (6)115°．(7)36°．(8)30°，45°，105°． 8．35°． 9．(1)10°；(2) 10．(1)113°，(2) (3)116°． 11．(1)23°．(2) 证明：∵OB平分∠ABC，OC平分∠ACE， ∴ ∴ 12． 13．36°． 14．39°． 由本练习中第4题结论可知： ∠C＋∠CDM＝∠M＋∠MBC， 即 同理， 由①、②得 因此∠C＝39°．