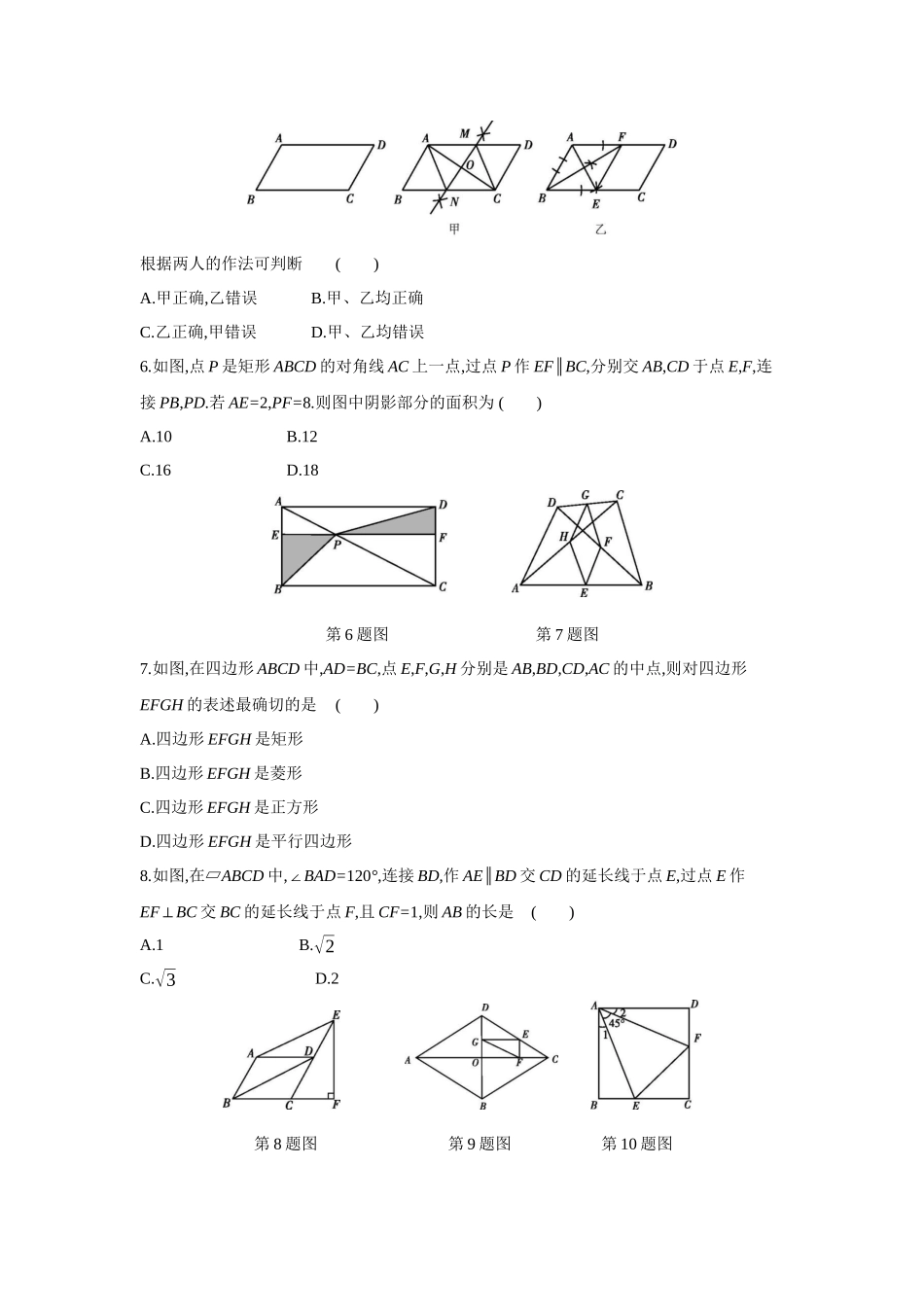
第十八章平行四边形一、选择题(每题3分,共30分)1.下列命题正确的是()A.一组对边平行,另一组对边相等的四边形是平行四边形B.对角线互相垂直的四边形是菱形C.对角线相等的四边形是矩形D.一组邻边相等的矩形是正方形2.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,AB边的中点,连接EF.若EF=√3,OC=2,则菱形ABCD的面积为()A.2√3B.4√3C.6√3D.8√3第2题图第3题图第4题图3.如图,在矩形ABCD中,AE平分∠BAD,交边BC于点E,若ED=5,EC=3,则矩形ABCD的周长为()A.11B.14C.22D.284.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=√3,AC=2,BD=4,则AE的长为()A.√32B.32C.√217D.2√2175.如图,在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形.乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断()A.甲正确,乙错误B.甲、乙均正确C.乙正确,甲错误D.甲、乙均错误6.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10B.12C.16D.18第6题图第7题图7.如图,在四边形ABCD中,AD=BC,点E,F,G,H分别是AB,BD,CD,AC的中点,则对四边形EFGH的表述最确切的是()A.四边形EFGH是矩形B.四边形EFGH是菱形C.四边形EFGH是正方形D.四边形EFGH是平行四边形8.如图,在▱ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是()A.1B.√2C.√3D.2第8题图第9题图第10题图9.如图,四边形ABCD是菱形,BD=4√2,AD=2√6,点E是CD边上的一动点,过点E作EF⊥OC于点F,EG⊥OD于点G,连接FG,则FG的最小值为()A.52B.125C.4√33D.√610.如图,正方形ABCD的边长为1,∠EAF=45°,AE=AF,给出下列结论:①1∠=2∠=22.5°;②点C到EF的距离是√2-1;③△ECF的周长为2;BE+DF>EF.④其中正确的结论有()A.4个B.3个C.2个D.1个二、填空题(每题3分,共18分)11.工人师傅在做门窗或矩形零件时,不仅要测量两组对边是否相等,还要测量两条对角线是否相等,这样做的依据是.12.如图,E为▱ABCD外一点,且EB⊥BC于点B,ED⊥CD于点D,若∠E=50°,则∠A的度数为.第12题图第13题图第14题图13.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为.14.如图,点P是矩形ABCD的边AD上一动点,矩形的两条边AB,B...