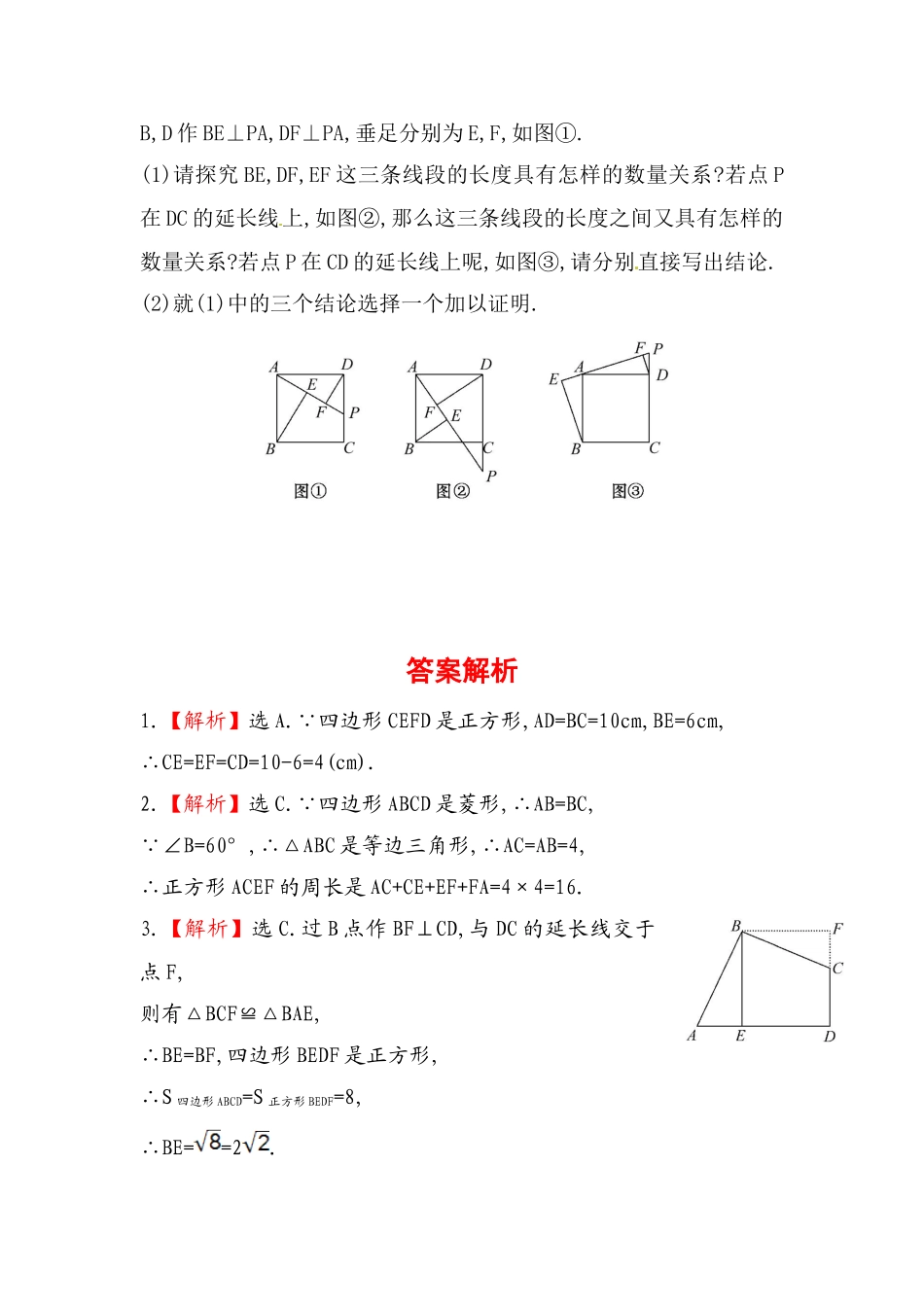
正方形一、选择题(每小题4分,共12分)1.如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=()A.4cmB.6cmC.8cmD.10cm2.(2013·凉山州中考)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为()A.14B.15C.16D.17[来源:www.shulihua.net]3.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=()A.2B.3C.2D.2二、填空题(每小题4分,共12分)4.如图正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是.5.如图,已知正方形ABCD的边长为1,连接AC,BD,相交于点O,CE平分∠ACD交BD于点E,则DE=.6.(2013·绵阳中考)对正方形ABCD进行分割,如图1,其中E,F分别是BC,CD的中点,M,N,G分别是OB,OD,EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为.[来源:数理化网]三、解答题(共26分)7.(8分)(2013·黔东南州中考)如图,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证:AM=EF.8.(8分)如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB,AC上的一动点,且满足BP=AQ,D是BC的中点.(1)求证:△PDQ是等腰直角三角形.(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.【拓展延伸】9.(10分)在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B,D作BE⊥PA,DF⊥PA,垂足分别为E,F,如图①.(1)请探究BE,DF,EF这三条线段的长度具有怎样的数量关系?若点P在DC的延长线上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?若点P在CD的延长线上呢,如图③,请分别直接写出结论.(2)就(1)中的三个结论选择一个加以证明.[来源:www.shulihua.net]答案解析1.【解析】选A. 四边形CEFD是正方形,AD=BC=10cm,BE=6cm,∴CE=EF=CD=10-6=4(cm).2.【解析】选C. 四边形ABCD是菱形,∴AB=BC, ∠B=60°,∴△ABC是等边三角形,∴AC=AB=4,∴正方形ACEF的周长是AC+CE+EF+FA=4×4=16.3.【解析】选C.过B点作BF⊥CD,与DC的延长线交于点F,则有△BCF≌△BAE,∴BE=BF,四边形BEDF是正方形,∴S四边形ABCD=S正方形BEDF=8,∴BE==2.4.【解析】由SSS知△ABE≌△ADF,∴∠BAE=∠DAF,当△AEF在正方形内部时,∠BAE=15°,当△AEF在正方形外部时,如图∠BAE+∠DAF=330°,∴∠BAE=165°.答案:15°或165°5.【解析】过E作EF⊥DC于点F. 四边形ABCD是...