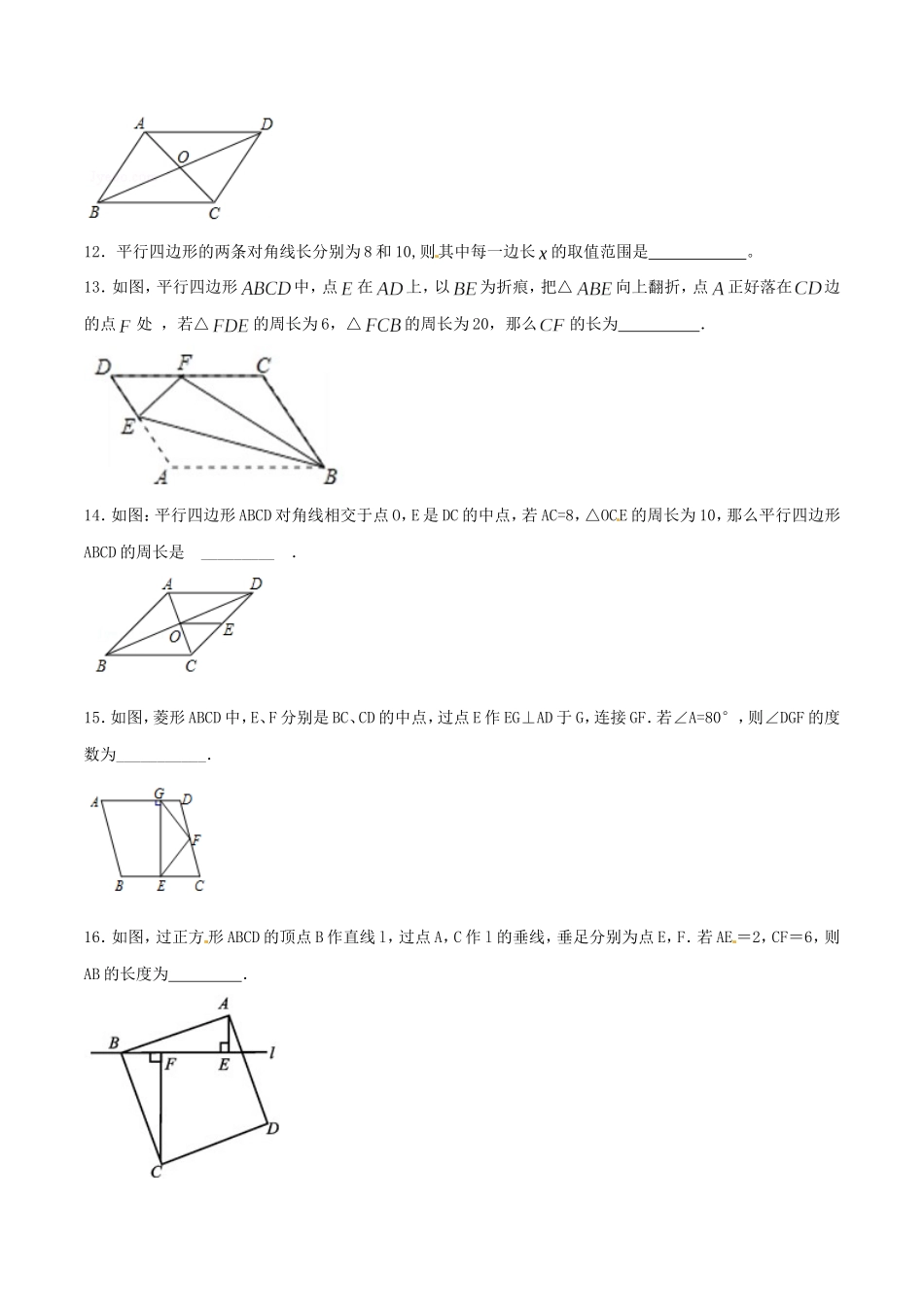
《第十八章平行四边形》测试卷(A卷)(测试时间:90分钟满分:120分)一.选择题(共10小题,每题3分,共30分)1.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是()2.下列命题中正确的是()A.有一组邻边相等的四边形是菱形B.有一个角是直角的平行四边形是矩形C.对角线垂直的平行四边形是正方形D.一组对边平行的四边形是平行四边形3.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=()A.40°B.50°C.60°D.80°4.如图,在中,AD=8,点E,F分别是BD,CD的中点,则EF等于()A.2B.3C.4D.55.已知一矩形的两边长分别为7cm和12cm,其中一个内角的平分线分长边为两部分,这两部分的长分别为().A.6cm和6cmB.7cm和5cmC.4cm和8cmD.3cm和9cm6.在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC于E,则AE=()A、4B、5C、4.8D、2.47.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是()A.2cm<OA<5cmB.2cm<OA<8cmC.1cm<OA<4cmD.3cm<OA<8cm8.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()[来源:学科网]A.14B.15C.16D.179.如图所示,将一张边长为8的正方形纸片折叠,使点落在的中点处,点落在点处,折痕为,则线段的长为()A.10B.4C.D.10.已知在四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC②AD=BC③OA=OC④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有()A.2种B.3种C.4种D.5种二、填空题(共10小题,每题3分,共30分)11.如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件:,使四边形ABCD为平行四边形(不添加任何辅助线).12.平行四边形的两条对角线长分别为8和10,则其中每一边长x的取值范围是。13.如图,平行四边形中,点在上,以为折痕,把△向上翻折,点正好落在边的点处,若△的周长为6,△的周长为20,那么的长为.14.如图:平行四边形ABCD对角线相交于点O,E是DC的中点,若AC=8,△OCE的周长为10,那么平行四边形ABCD的周长是_________.15.如图,菱形ABCD中,E、F分别是BC、CD的中点,过点E作EG⊥AD于G,连接GF.若∠A=80°,则∠DGF的度数为___________.[来源:Zxxk.Com]16.如图,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为点E,F.若AE=2,CF=6,则AB的长度为.17.如图,将两条宽度...