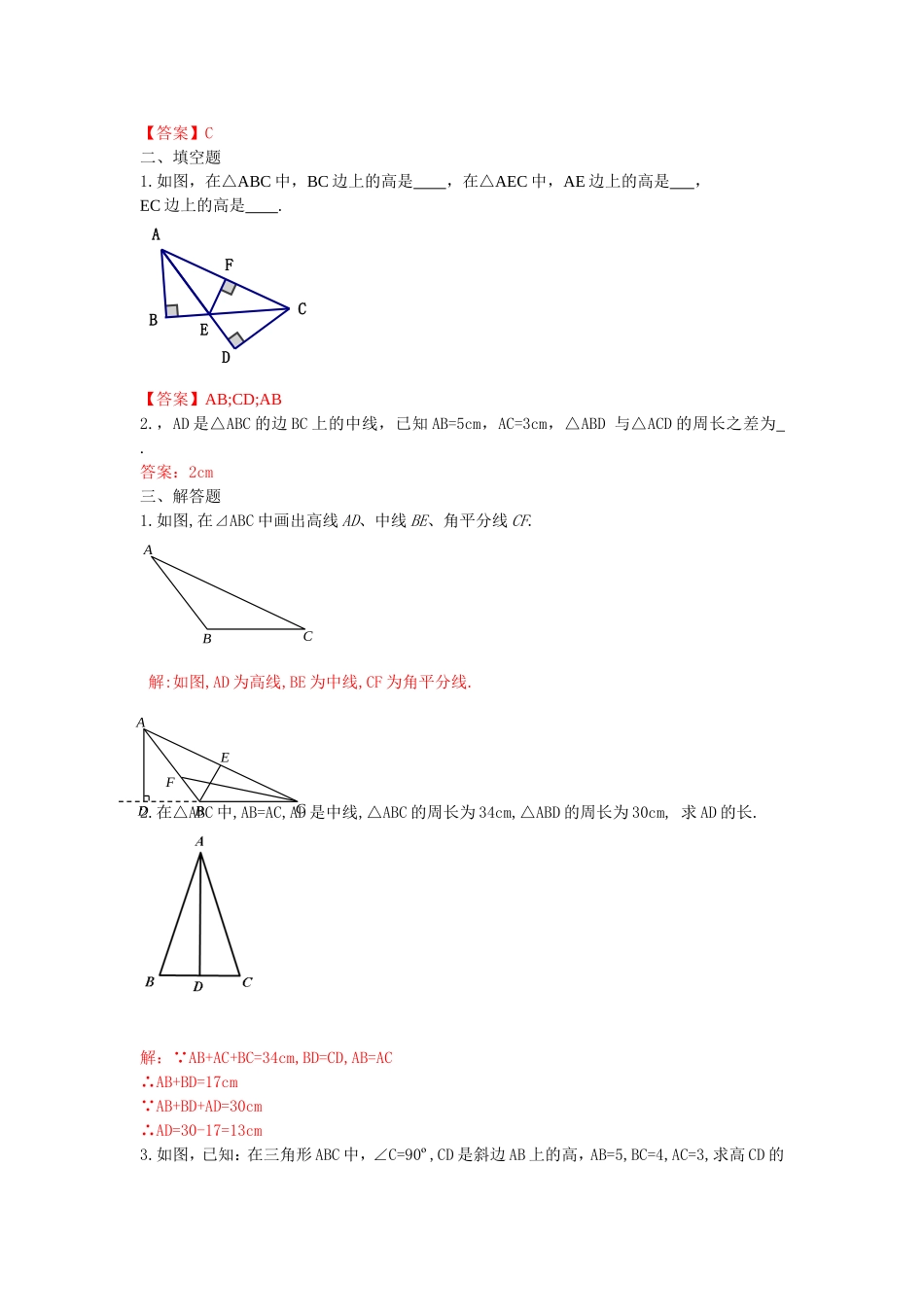
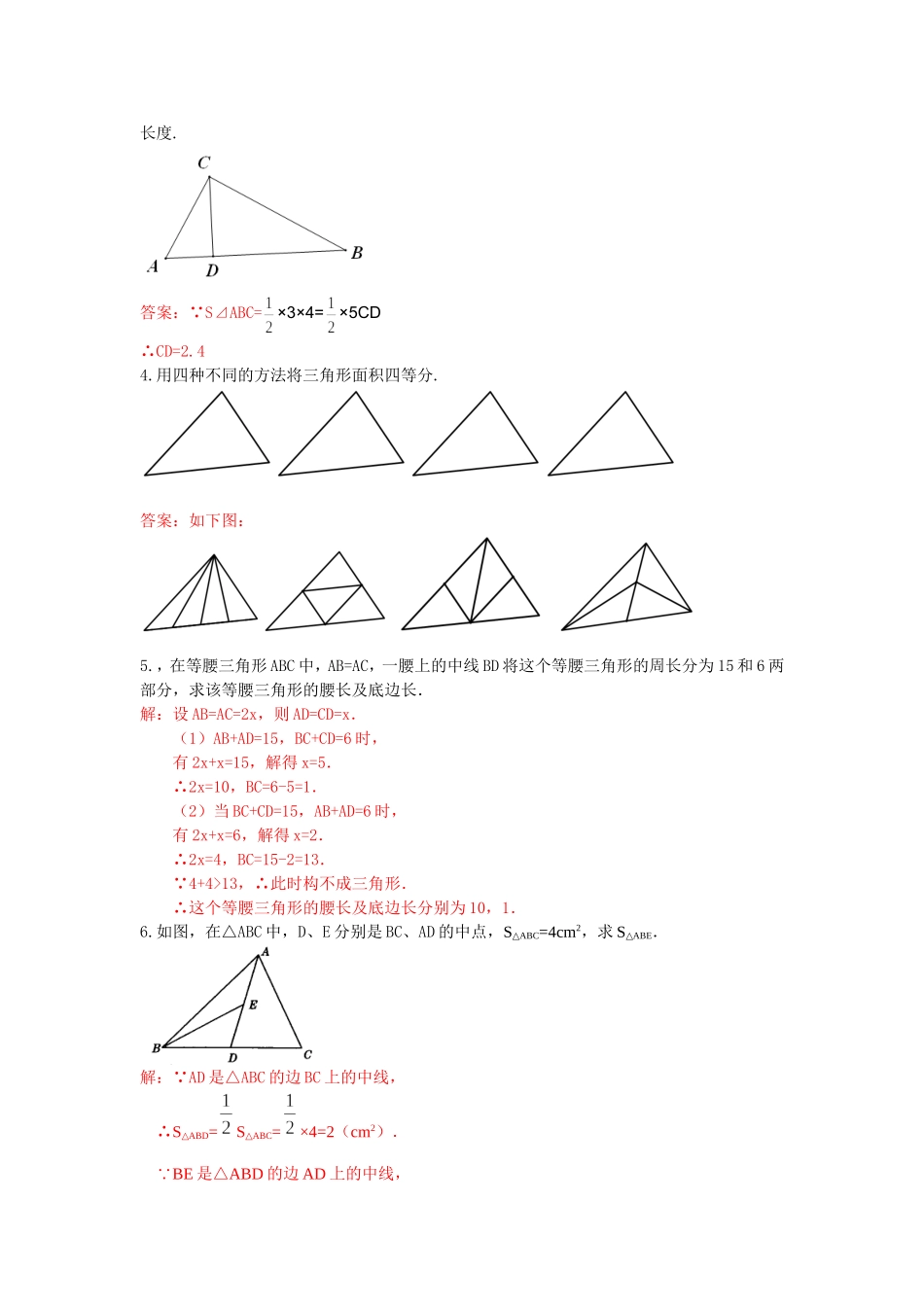
11.1.2 三角形的高、中线与角平分线 练习.doc

11.1.2三角形的高、中线与角平分线 基础知识 一、选择题 1.三角形的角平分线、中线、高线都是（ ） A.线段 B.射线 C.直线 D.以上都有可能 【答案】A 2.至少有两条高在三角形内部的三角形是（ ） A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D.都有可能 【答案】A 3.(2012 山东省德州市) 不一定在三角形内部的线段是（ ） （A）三角形的角平分线 （B）三角形的中线 （C）三角形的高 （D）三角形的中位线 【答案】C 4.在△ABC中，D是BC上的点，且BD:CD=2:1,S△ACD=12,那么S△ABC等于（ ） A. 30 B. 36 C. 72 D.24 【答案】B 5.小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解．”小华根据小明的提示作出的图形正确的是（　　） A. B. C. D. 【答案】A 6．可以把一个三角形分成面积相等的两部分的线段是（　　） A．三角形的高 B．三角形的角平分线 C．三角形的中线 D．无法确定 【答案】C 7．在三角形中，交点一定在三角形内部的有（　　） ①三角形的三条高线 ②三角形的三条中线 ③三角形的三条角平分线 ④三角形的外角平分线． A．①②③④ B．①②③ C．①④ D．②③ 【答案】D 8. 如果一个三角形三条高的交点恰是三角形的一个顶点，那么这个三角形是 （ ） A. 锐角三角形 B. 直角三角形 C.钝角三角形 D.不能确定 【答案】B 9．下图中，正确画出△ABC的 AC边上的高的是 （ ） A B C D 【答案】C 二、填空题 1.如图，在△ABC中，BC边上的高是 ，在△AEC中，AE边上的高是 ， EC边上的高是 . 【答案】AB;CD;AB 2. ，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm，△ABD与△ACD的周长之差为 . 答案：2cm 三、解答题 1.如图,在⊿ABC中画出高线AD、中线BE、角平分线CF. 解:如图,AD为高线,BE为中线,CF为角平分线. 　　　 2.在△ABC中,AB=AC,AD是中线,△ABC的周长为34cm,△ABD的周长为30cm, 求AD的长. 解：∵AB+AC+BC=34cm,BD=CD,AB=AC ∴AB+BD=17cm ∵AB+BD+AD=30cm ∴AD=30-17=13cm 3. 如图，已知：在三角形ABC中，∠C=90º,CD是斜边AB上的高，AB=5,BC=4,AC=3,求高CD的长度. 答案：∵S⊿ABC=×3×4=×5CD ∴CD=2.4 4.用四种不同的方法将三角形面积四等分. 答案：如下图： 5.，在等腰三角形ABC中，AB=AC，一腰上的中线BD将这个等腰三角形的周长分为15和6两部分，求该等腰三角形的腰长及底边长． 解：设AB=AC=2x，则AD=CD=x． （1）AB+AD=15，BC+CD=6时， 有2x+x=15，解得x=5． ∴2x=10，BC=6-5=1． （2）当BC+CD=15，AB+AD=6时， 有2x+x=6，解得x=2． ∴2x=4，BC=15-2=13． ∵4+4>13，∴此时构不成三角形． ∴这个等腰三角形的腰长及底边长分别为10，1． 6.如图，在△ABC中，D、E分别是BC、AD的中点，S△ABC=4cm2，求S△ABE． 解：∵AD是△ABC的边BC上的中线， ∴S△ABD=S△ABC=×4=2（cm2）． ∵BE是△ABD的边AD上的中线， ∴S△ABE=S△ABD=×2=1（cm2）． 7．如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm， 求：（1）△ABC的面积； （2）CD的长； （3）作出△ABC的边AC上的中线BE，并求出△ABE的面积； （4）作出△BCD的边BC边上的高DF，当BD=11cm 时，试求出DF的长。 【答案】(1)30（2）（3）15（4） 【解析】解：(1)∵∠ACB=90°，BC=12cm，AC=5cm， ∴S△ABC = (2) ∵CD是AB边上的高， ∴ ∵ AB=13cm ，S△ABC =30cm2 ∴ CD = cm （3）作图略 ∵ BE为AC边上的中线 ∴ ∵ S△ABC =30cm2 ∴ （4）作图略 ∵ ∴ ∵ ∴ [来+科+网Z+X+X+K] 能力提升 1.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点, 且S △ABC=4cm2,则S阴影等于( ) A.2cm2 B.1cm2 C.cm2 D.cm2 【答案】B 2.如图，S△ABC=1,且D是BC的中点，AE:EB=1:2,求△ADE的面积. 【答案】 S△ADE=S△ABD=S△ABC= 3.如图,在中,,的高与的比是多少? (友情提示:利用三角形的面积公式) 解:∵ ∴ ∵ ∴ ∴