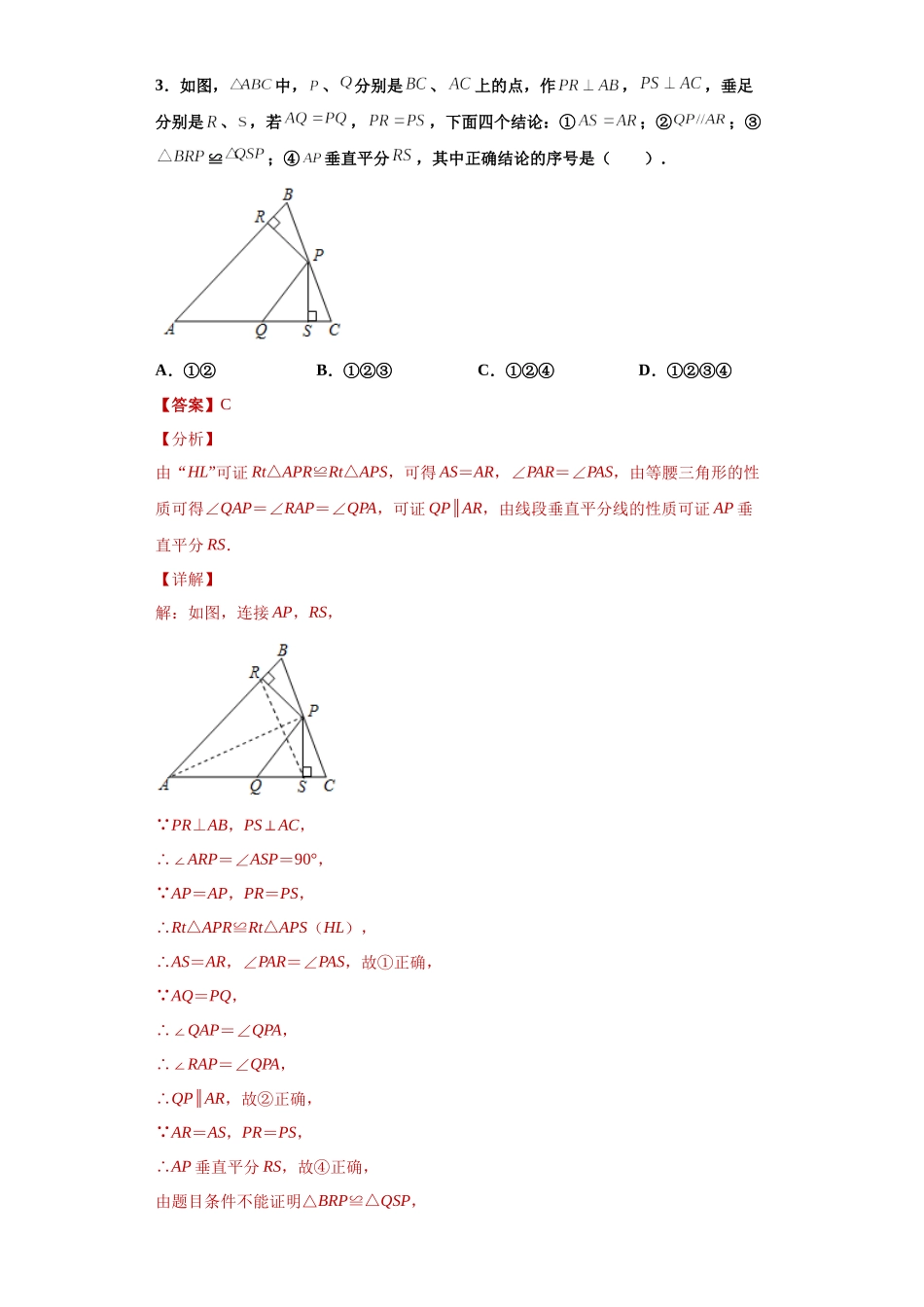
第一学期人教版八年级数学期末模拟卷三(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题(共30分)1.在一次数学课上,老师让学生进行画图,你觉得学生可能会发现的结论是()A.三条线段首尾顺次相接能构成三角形B.三角形的内角和是180°C.三角形的任意一个外角大于和它不相邻的内角D.三角形任意两边之和大于第三边【答案】D【分析】根据三角形两边之和大于第三边判断即可.【详解】解:① a=8,b=5,c=1,∴a>b+c,∴三条线段不能组成三角形;② a=8,b=6,c=2,∴a=b+c,∴三条线段不能组成三角形;③ a=8,b=6,c=3,∴a<b+c,∴三条线段能组成三角形;∴学生可能会发现的结论是三角形任意两边之和大于第三边,故选:D.【点睛】本题主要考查了三角形三边关系的应用,准确判断是解题的关键.2.如图,直线AB//CD,直线AB,EG交于点F,直线CD,PM交于点N,∠FGH=90°,∠CNP=30°,∠EFA=α,∠GHM=β,∠HMN=γ,则下列结论正确的是(更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com)A.β=α+γB.α+β+γ=120°C.α+β﹣γ=60°D.β+γ﹣α=60°【答案】C【分析】延长HG交直线AB于点K,延长PM交直线AB于点S.利用平行线的性质求出∠KSM,利用邻补角求出∠SMH,利用三角形的外角与内角的关系,求出∠SKG,再利用四边形的内角和求出∠GHM.【详解】解:延长HG交直线AB于点K,延长PM交直线AB于点S. AB∥CD,∴∠KSM=∠CNP=30°. ∠EFA=∠KFG=α,∠KGF=180°-∠FGH=90°,∠SMH=180°-∠HMN=180°-γ,∴∠SKH=∠KFG+∠KGF=α+90°, ∠SKH+∠GHM+∠SMH+∠KSM=360°,∴∠GHM=360°-α-90°-180°+γ-30°,∴α+β-γ=60°,故选:C.【点睛】本题考查了平行线的性质、三角形的外角与内角的关系及多边形的内角和定理等知识点.利用平行线、延长线把分散的角集中在四边形中是解决本题的关键.3.如图,中,、分别是、上的点,作,,垂足分别是、,若,,下面四个结论:①;②;③≌;④垂直平分,其中正确结论的序号是().A.①②B.①②③C.①②④D.①②③④【答案】C【分析】由“HL”可证Rt△APR≌Rt△APS,可得AS=AR,∠PAR=∠PAS,由等腰三角形的性质可得∠QAP=∠RAP=∠QPA,可证QP∥AR,由线段垂直平分线的性质可证AP垂直平...