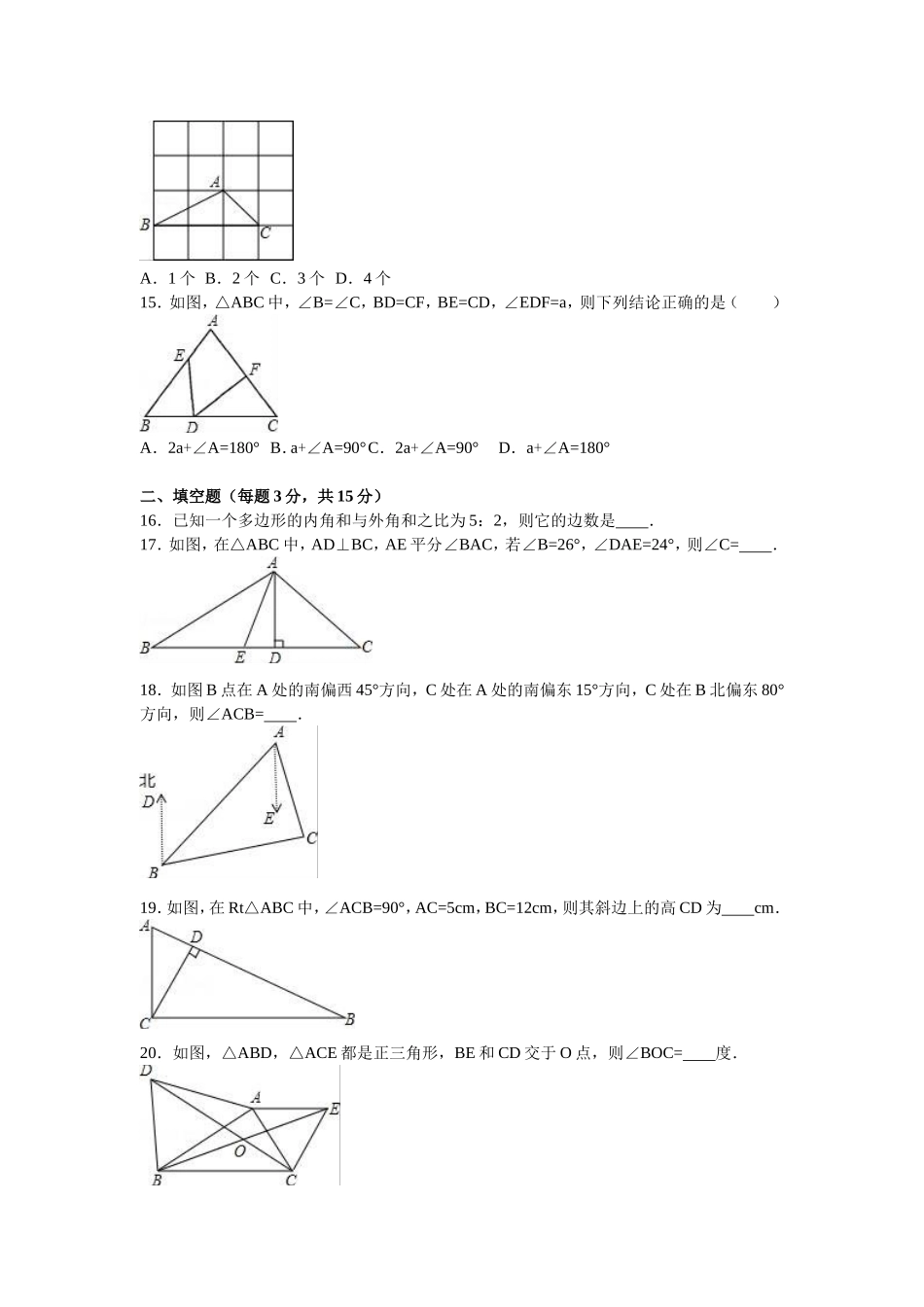
八年级(上)第一次月考数学试卷一、选择题(每题2分,共30分)1.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()A.5B.6C.11D.162.适合条件∠A=∠B=∠C的三角形是()A.锐角三角形B.等边三角形C.钝角三角形D.直角三角形3.如果CD平分含30°三角板的∠ACB,则∠1等于()A.110°B.105°C.100°D.95°4.下列说法错误的是()A.一个三角形中至少有一个角不少于60°B.三角形的中线不可能在三角形的外部C.三角形的中线把三角形的面积平均分成相等的两部分D.直角三角形只有一条高5.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSSB.SASC.AASD.ASA6.下列说法:①全等三角形的形状相同、大小相等②全等三角形的对应边相等、对应角相等③面积相等的两个三角形全等④全等三角形的周长相等其中正确的说法为()A.①②③④B.①②③C.②③④D.①②④7.如图,∠BAC=40°,AD平分∠BAC,BD∥AC,则∠D的度数为()A.20°B.30°C.40°D.50°8.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是()A.180°B.220°C.240°D.300°9.如果一个多边形的每一个内角都是135°,那么这个多边形的边数是()A.5B.6C.8D.1010.已知图中的两个三角形全等,则∠α的度数是()A.72°B.60°C.58°D.50°11.在△ABC和△FED中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件()A.AB=EDB.AB=FDC.AC=FDD.∠A=∠F12.如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是()A.15°B.25°C.30°D.10°13.如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为()A.15°B.20°C.25°D.30°14.△ABC是格点三角形(顶点在网格线的交点),则在图中能够作出△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是()A.1个B.2个C.3个D.4个15.如图,△ABC中,∠B=∠C,BD=CF,BE=CD,∠EDF=a,则下列结论正确的是()A.2a+∠A=180°B.a+∠A=90°C.2a+∠A=90°D.a+∠A=180°二、填空题(每题3分,共15分)16.已知一个多边形的内角和与外角和之比为5:2,则它的边数是.17.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠B=26°,∠DAE=24°,则∠C=...