13.3 等腰三角形 课后训练.doc

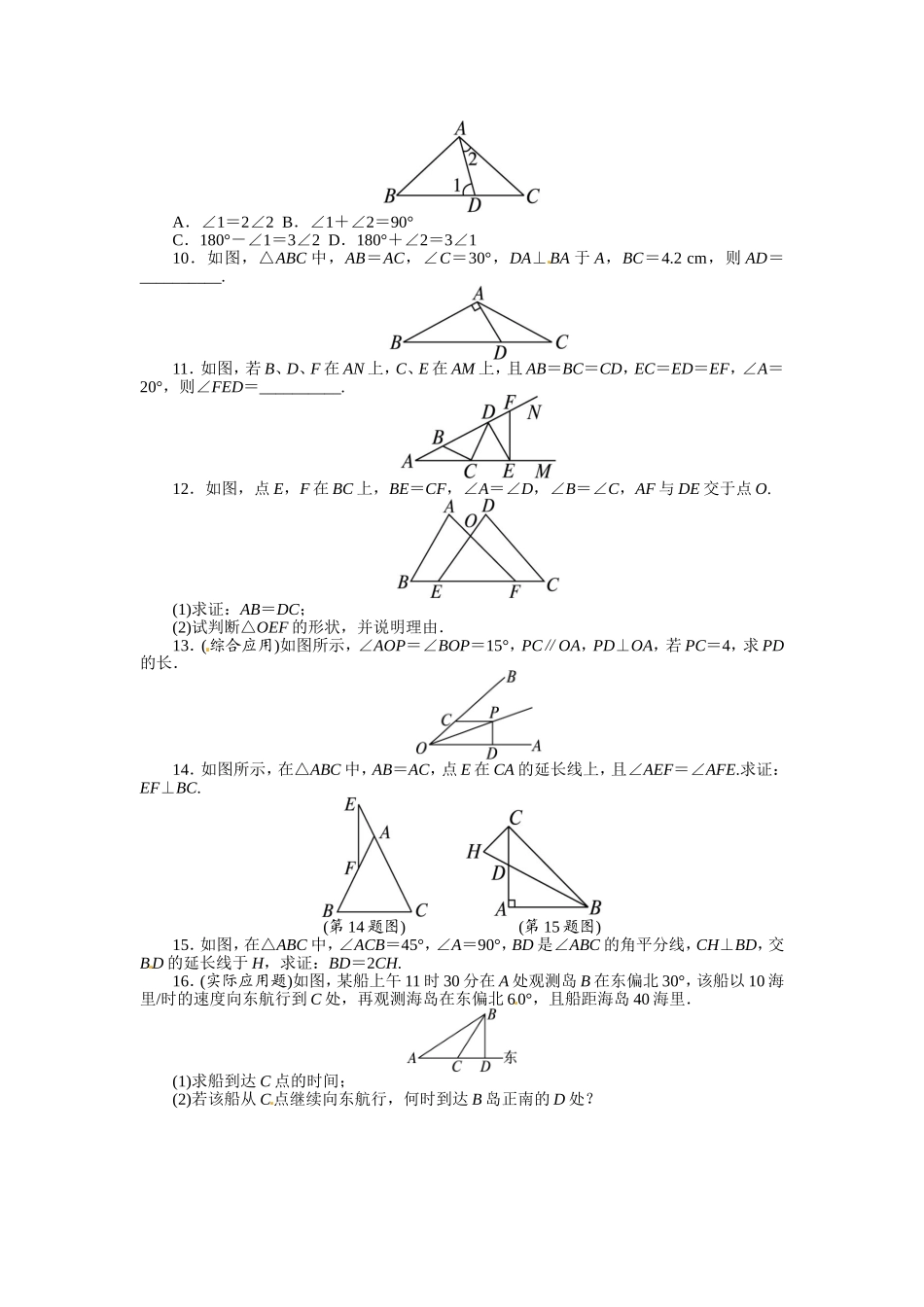
课后训练 基础巩固 1．若等腰三角形底角为72°，则顶角为 (　　)． A．108° B．72° C．54° D．36° 2．如图，在△ABC中，AB＝AC，AD＝BD＝BC，则∠C＝(　　)． A．72° B．60° C．75° D．45° 3．若等腰三角形的周长为26 cm，一边为11 cm，则腰长为(　　)． A．11 cm B．7.5 cm C．11 cm或7.5 cm D．以上都不对 4．下列三角形：①有两个角等于60°的三角形；②有一个角等于60°的等腰三角形；③三个外角(每个顶点处各取一个外角)都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有(　　)． A．①②③ B．①②④ C．①③ D．①②③④ 5．如图所示，已知∠1＝∠2，要使BD＝CD，还应增加的条件是(　　)． ①AB＝AC　②∠B＝∠C　③AD⊥BC　④AB＝BC A．① B．①② C．①②③ D．①②③④ 6．如图所示，在△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB于点D，若AD＝2，则AB＝__________. 能力提升 7．如图，在△ABC中，AB＝AC，BD和CD分别是∠ABC和∠ACB的平分线，EF过D点，且EF∥BC，图中等腰三角形共有(　　)． A．2个 B．3个 C．4个 D．5个 8．如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是(　　)． A．6 B．7 C．8 D．9 9．如图，D是△ABC中BC边上一点，AB＝AC＝BD，则∠1和∠2的关系是(　　)． A．∠1＝2∠2 B．∠1＋∠2＝90° C．180°－∠1＝3∠2 D．180°＋∠2＝3∠1 10．如图，△ABC中，AB＝AC，∠C＝30°，DA⊥BA于A，BC＝4.2 cm，则AD＝__________. 11．如图，若B、D、F在AN上，C、E在AM上，且AB＝BC＝CD，EC＝ED＝EF，∠A＝20°，则∠FED＝__________. 12．如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O. (1)求证：AB＝DC； (2)试判断△OEF的形状，并说明理由． 13．(综合应用)如图所示，∠AOP＝∠BOP＝15°，PC∥OA，PD⊥OA，若PC＝4，求PD的长． 14．如图所示，在△ABC中，AB＝AC，点E在CA的延长线上，且∠AEF＝∠AFE.求证：EF⊥BC. (第14题图) (第15题图) 15．如图，在△ABC中，∠ACB＝45°，∠A＝90°，BD是∠ABC的角平分线，CH⊥BD，交BD的延长线于H，求证：BD＝2CH. 16．(实际应用题)如图，某船上午11时30分在A处观测岛B在东偏北30°，该船以10海里/时的速度向东航行到C处，再观测海岛在东偏北60°，且船距海岛40海里． (1)求船到达C点的时间； (2)若该船从C点继续向东航行，何时到达B岛正南的D处？ 参考答案 1．D　点拨：等腰三角形两底角相等，所以顶角为36°，故选D. 2．A　点拨：设∠A＝x，由已知可知，∠BDC＝∠C＝∠ABC＝2∠A＝2x， 因为∠A＋∠ABC＋∠C＝180°， 所以x＋2x＋2x＝180°. 解得x＝36°，所以∠C＝72°，故选A. 3．C　点拨：边长为11 cm的边长可能是腰，也可能是底，所以要分两种情况讨论．一种情况腰长为11 cm；另一种情况底边为11 cm，此时腰长为7.5 cm，两种情况都成立，故选C. 4．D　点拨：①②为判定定理，③每个外角都相等，则都是120°，所以每个内角都是60°，④一腰上的中线也是这条腰上的高，说明这条线段所在的直线是这条腰的垂直平分线，所以腰等于底，也是等边三角形，四个都成立，故选D. 5．C　点拨：①②说明△ABC为等腰三角形，由“三线合一”可知BD＝CD，由③能得到△ABD≌△ACD，所以BD＝CD，④不能得到BD＝CD，故选C. 6．8　点拨：由题意可知，在Rt△ACD和Rt△ABC中，∠ACD＝∠B＝30°， 所以AC＝2AD，AB＝2AC. 所以AB＝4AD＝4×2＝8. 7．D　点拨：由题意知，AB＝AC，AE＝AF，BE＝DE，CF＝DF，BD＝CD，所以所有的三角形都是等腰三角形，共有5个，故选D. 8．C　点拨：如图，共有8个格点．注意3和8也是，故选C. 9．D　点拨：因为AB＝BD， 所以∠B＝180°－2∠1，∠C＝∠1－∠2. 因为AB＝AC， 所以∠B＝∠C. 所以180°－2∠1＝∠1－∠2， 整理得180°＋∠2＝3∠1，故选D. 10．1.4 cm　点拨：由已知可以推出∠B＝∠CAD＝∠C＝30°，AD＝DC，∠C＝30°，DA⊥BA于A，所以BD＝2AD. 所以BC＝3DC＝3AD＝4.2(cm)． 所以AD＝1.4 cm. 11．20°　点拨：运用一个外角等于和它不相邻的内角，及等腰三角形两底角相等可求出∠FED＝20°. 12．(1)证明：∵BE＝CF， ∴BE＋EF＝CF＋EF，即BF＝CE. 又∵∠A＝∠D，∠B＝∠C， ∴△ABF≌△DCE(AAS)． ∴AB＝DC. (2)解：△OEF为等腰三角形， 理由如下： ∵△ABF≌△DCE， ∴∠AFB＝∠DEC.∴OE＝OF. ∴△OEF为等腰三角形． 13．解：如图，过P作PE⊥OB，垂足为E. ∵∠AOP＝∠BOP＝15°，PD⊥OA， ∴PD＝PE. ∵PC∥OA，∴∠CPO＝∠AOP＝15°. ∴∠BCP＝∠BOP＋∠CPO＝30°， 在Rt△CPE中，∠BCP＝30°， ∴PE＝. ∴PD＝PE＝2. 14．证明：如图，过A作AD⊥BC，垂足为D， ∵AB＝AC， ∴∠BAD＝. ∵∠AEF＝∠AFE， ∠BAC＝∠AEF＋∠AFE， ∴∠EFA＝. ∴∠EFA＝∠BAD. ∴EF∥AD，∴EF⊥BC. 15．证明：如图，延长CH、BA交于点E. ∵CH⊥BD，BD是∠ABC的角平分线， ∴∠CHB＝∠EHB＝90°，∠CBH＝∠EBH. 又∵BH＝BH，∴△CBH≌△EBH. ∴CH＝EH.∴CE＝2CH. ∵∠ACB＝45°，∠CAB＝90°， ∴∠ABC＝45°， ∴∠ACB＝∠ABC.∴AC＝AB. ∵∠CAB＝∠CAE＝90°， ∴∠E＋∠ECA＝90°. ∵CH⊥BD，∴∠E＋∠EBH＝90°. ∴∠ECA＝∠EBH.∴△ECA≌△DBA. ∴CE＝BD.∴BD＝2CH. 16．解：(1)∵∠A＝30°，∠BCD＝60°， ∴∠ABC＝30°.∴∠A＝∠ABC. ∴AC＝BC＝40(海里),40÷10＝4(小时)． 答：船到达C点的时间是15时30分． (2)在Rt△BCD中，∠CBD＝30°， ∴CD＝×40＝20(海里),20÷10＝2(小时)． 答：该船在17时30分到达D处．