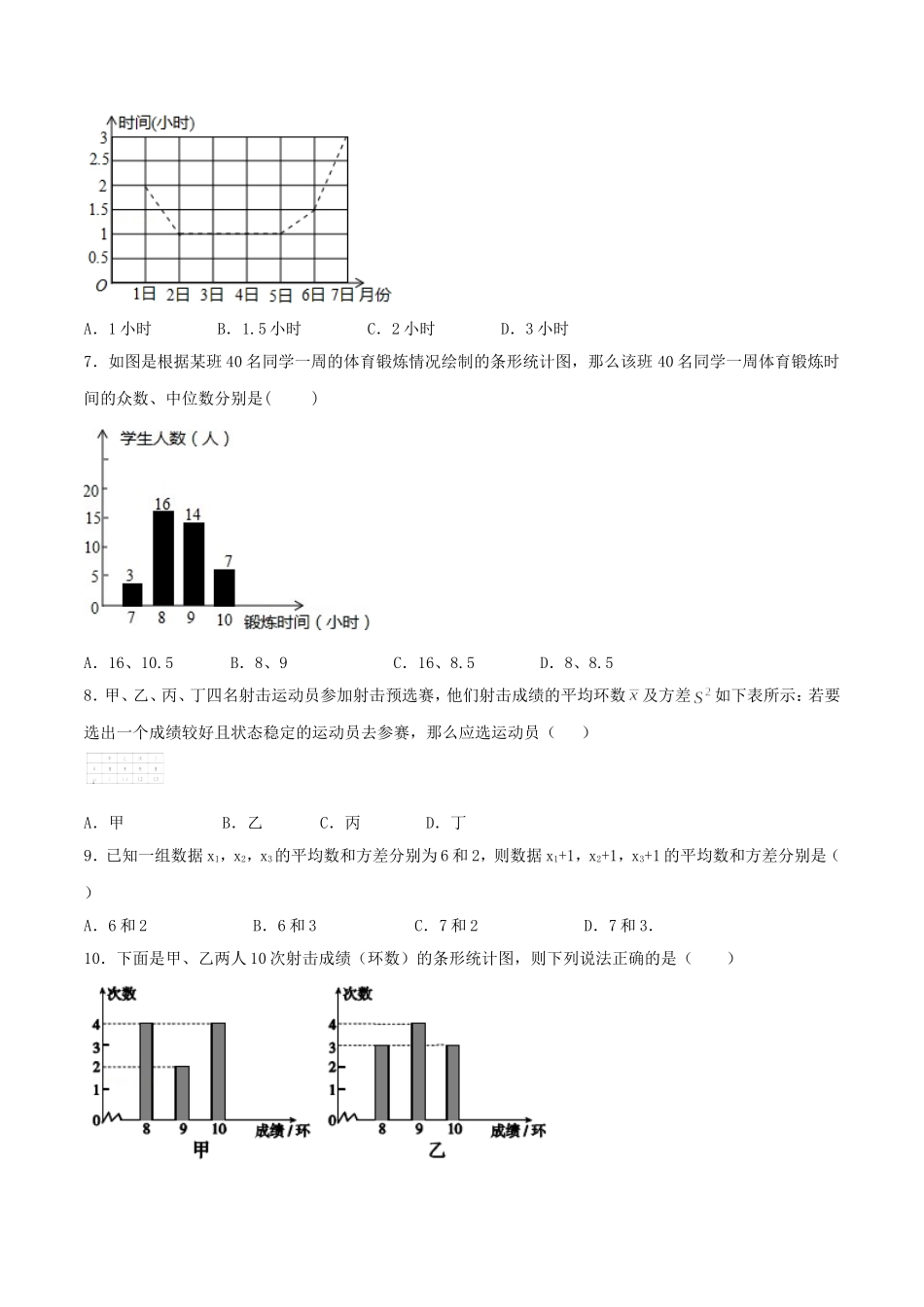
《第二十章数据的分析》测试卷(A卷)(测试时间:90分钟满分:120分)一.选择题(共10小题,每题3分,共30分)1.为响应“节约用水”的号召,小李随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是()A.8,8B.8.4,8C.8.4,8.4D.8,8.42.某班50名学生身高测量结果如下表:[来源:学|科|网]身高1.511.521.531.541.551.561.571.581.591.601.64人数1134[来源:学_科_网]34468106该班学生身高的众数和中位数分别是()A.1.60,1.56B.1.59,1.58C.1.60,1.58D.1.60,1.603.中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:时间(小时)5678人数1015205则这50名学生这一周在校的平均体育锻炼时间是()A.6.2小时B.6.4小时C.6.5小时D.7小时4.期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”,上面两位同学的话能反映处的统计量是()A.众数和平均数B.平均数和中位数C.众数和方差D.众数和中位数5.下表是某所学校一个学习小组一次数学测验的成绩统计表,已知该小组本次数学测验的平均分是85分,那么表中的的值是()分数708090100人数131A.4B.3C.2D.16.如图是小芹6月1日﹣7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是()A.1小时B.1.5小时C.2小时D.3小时7.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周体育锻炼时间的众数、中位数分别是()A.16、10.5B.8、9C.16、8.5D.8、8.58.甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均环数及方差如下表所示:若要选出一个成绩较好且状态稳定的运动员去参赛,那么应选运动员()A.甲B.乙C.丙D.丁9.已知一组数据x1,x2,x3的平均数和方差分别为6和2,则数据x1+1,x2+1,x3+1的平均数和方差分别是()A.6和2B.6和3C.7和2D.7和3.10.下面是甲、乙两人10次射击成绩(环数)的条形统计图,则下列说法正确的是()A.甲比乙的成绩稳定B.乙比甲的成绩稳定C.甲、乙两人的成绩一样稳定D.无法确定谁的成绩更稳定二、填空题(共10小题,每题3分,共30分)11.某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时...