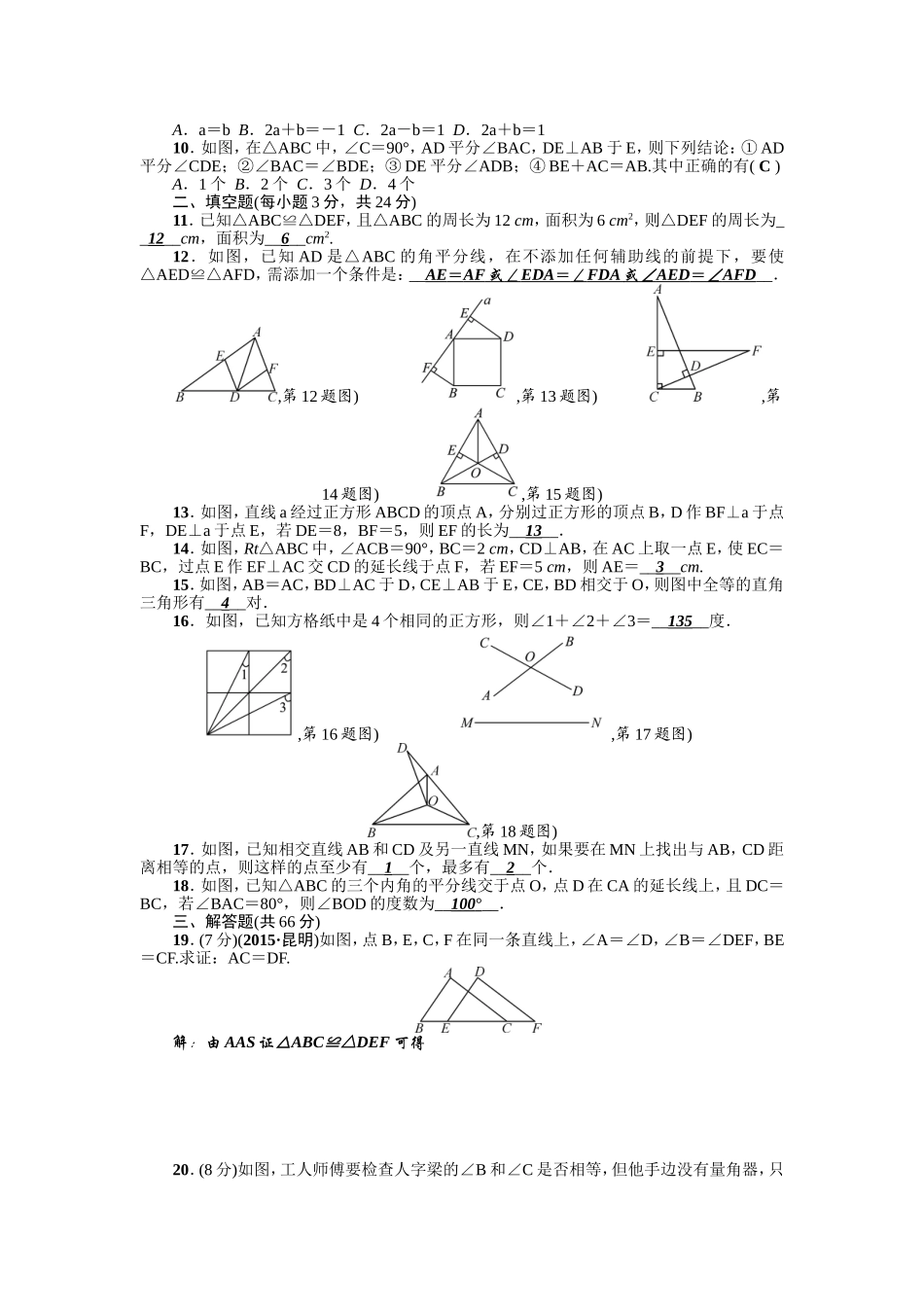
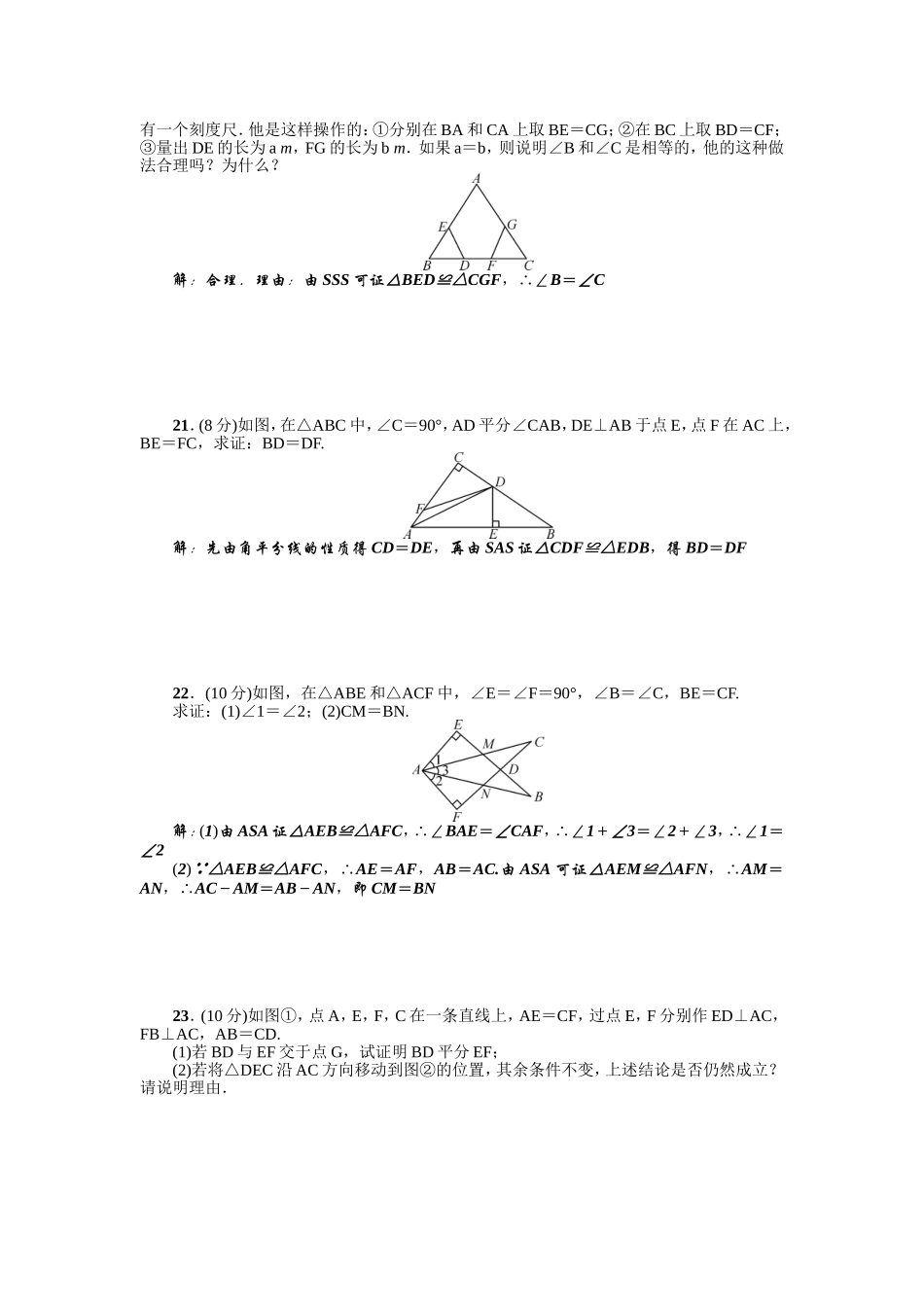
第十二章检测题(时间:100分钟满分:120分)一、选择题(每小题3分,共30分)1.如图,△ABC≌△EFD,且AB=EF,EC=4,CD=3,则AC=(C)A.3B.4C.7D.8,第1题图),第2题图),第3题图)2.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于(B)A.120°B.125°C.130°D.135°3.如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是(B)A.SASB.ASAC.AASD.SSS4.(2015·六盘水)如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是(D)A.∠A=∠DB.AB=DCC.∠ACB=∠DBCD.AC=BD,第4题图),第5题图),第6题图)5.如图,△ABC和△EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定△ABC≌△EDF的是(C)A.AB=EDB.AC=EFC.AC∥EFD.BF=DC6.如图,在△ABC中,∠B=42°,AD⊥BC于点D,点E是BD上一点,EF⊥AB于点F,若ED=EF,则∠AEC的度数为(D)A.60°B.62°C.64°D.66°7.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有(A)A.4个B.3个C.2个D.1个,第7题图),第8题图),第9题图),第10题图)8.如图,△ABC的三边AB,BC,CA的长分别为20,30,40,O是△ABC三条角平分线的交点,则S△ABO∶S△BCO∶S△CAO等于(C)A.1∶1∶1B.1∶2∶3C.2∶3∶4D.3∶4∶59.如图,在平面直角坐标系中,以点O为圆心,适当的长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为(B)A.a=bB.2a+b=-1C.2a-b=1D.2a+b=110.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB.其中正确的有(C)A.1个B.2个C.3个D.4个二、填空题(每小题3分,共24分)11.已知△ABC≌△DEF,且△ABC的周长为12cm,面积为6cm2,则△DEF的周长为__12__cm,面积为__6__cm2.12.如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:__AE=AF或∠EDA=∠FDA或∠AED=∠AFD__.,第12题图),第13题图),第14题图),第15题图)13.如图,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B,D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__13__.14.如图,R...