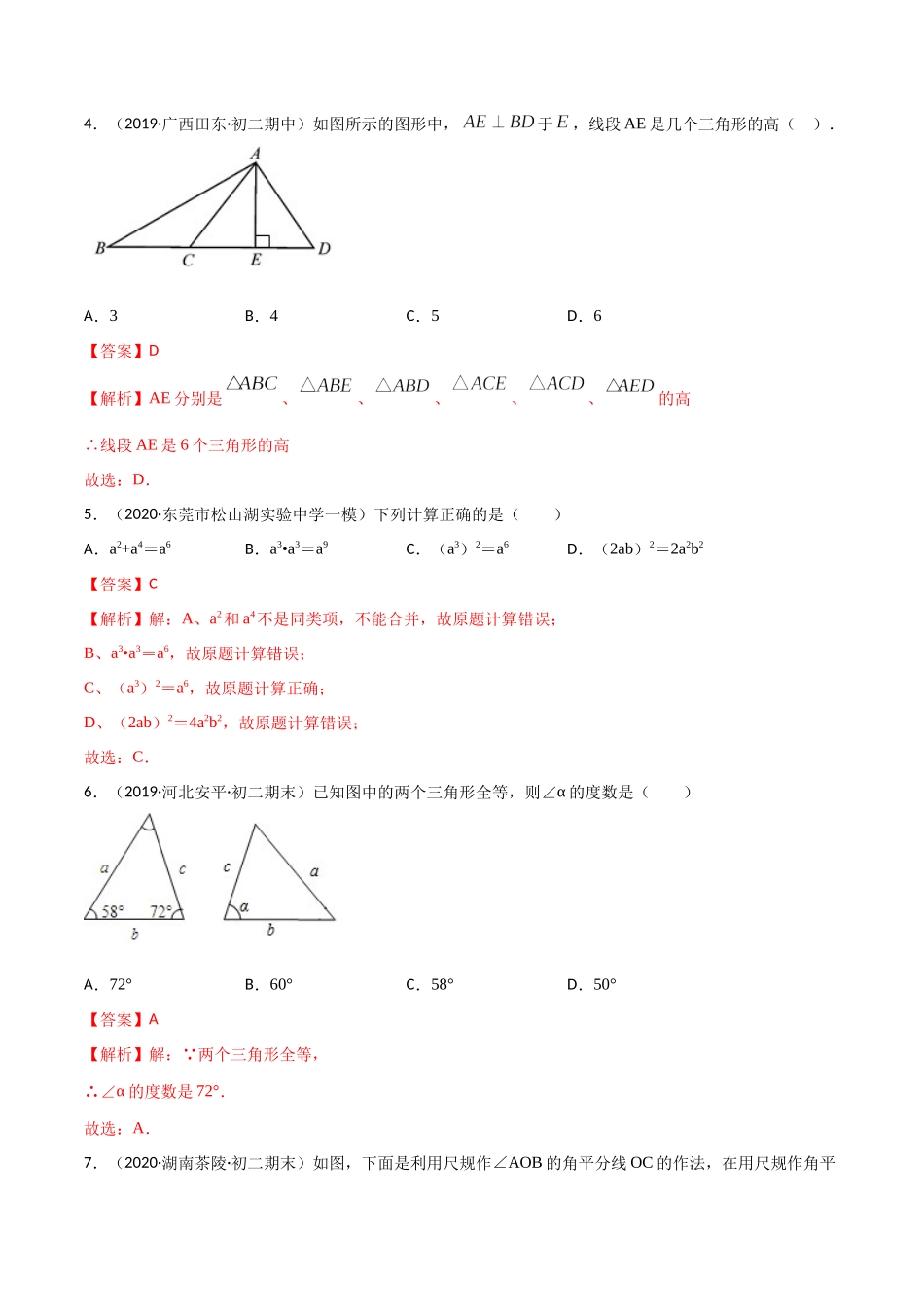
期中考试冲刺卷一一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)1.(2020·辽宁凌海·期末)下面每组数分别是三根小木棒的长度,用它们不能摆成一个三角形的是()A.5cm,10cm,5cmB.7cm,8cm,9cmC.3cm,4cm,5cmD.6cm,20cm,20cm【答案】A【解析】A、5+5=10,故以这三条线段不能构成三角形,选项正确;B、7+8>9,故以这三条线段能构成三角形,选项错误;C、3+4>5,故以这三条线段能构成三角形,选项错误;D、6+20>20,故以这三条线段可以构成三角形,选项错误,故选A.2.(2020·福建厦门一中初三月考)x7可以表示为().A.x3+x4B.x3·x4C.x14÷x2D.(x3)4【答案】B【解析】解:(A)x3与x4不是同类项,故A不可表示x7;(B)原式=x7,故B可表示x7;(C)原式=x12,故C不可表示x7;(D)原式=x12,故D不可表示x7;故选B.3.(2020·广东揭阳·初一期末)如图,已知△ABC≌△CDE,下列结论中不正确的是()A.AC=CEB.∠BAC=∠ECDC.∠ACB=∠ECDD.∠B=∠D【答案】C【解析】解:由全等三角形的性质可知A、B、D均正确,而∠ACB=∠CED,故C错误.故选择C.4.(2019·广西田东·初二期中)如图所示的图形中,于,线段AE是几个三角形的高().A.3B.4C.5D.6【答案】D【解析】AE分别是、、、、、的高∴线段AE是6个三角形的高故选:D.5.(2020·东莞市松山湖实验中学一模)下列计算正确的是()A.a2+a4=a6B.a3•a3=a9C.(a3)2=a6D.(2ab)2=2a2b2【答案】C【解析】解:A、a2和a4不是同类项,不能合并,故原题计算错误;B、a3•a3=a6,故原题计算错误;C、(a3)2=a6,故原题计算正确;D、(2ab)2=4a2b2,故原题计算错误;故选:C.6.(2019·河北安平·初二期末)已知图中的两个三角形全等,则∠α的度数是()A.72°B.60°C.58°D.50°【答案】A【解析】解: 两个三角形全等,∴∠α的度数是72°.故选:A.7.(2020·湖南茶陵·初二期末)如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是()作法:①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;②分别以D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于一点C;③画射线OC,射线OC就是∠AOB的角平分线.A.ASAB.SASC.SSSD.AAS【答案】C【解析】根据作图的过程知,在△EOC与△DOC中,,EOCDOC△≌△(SSS).故选C.8.(20...