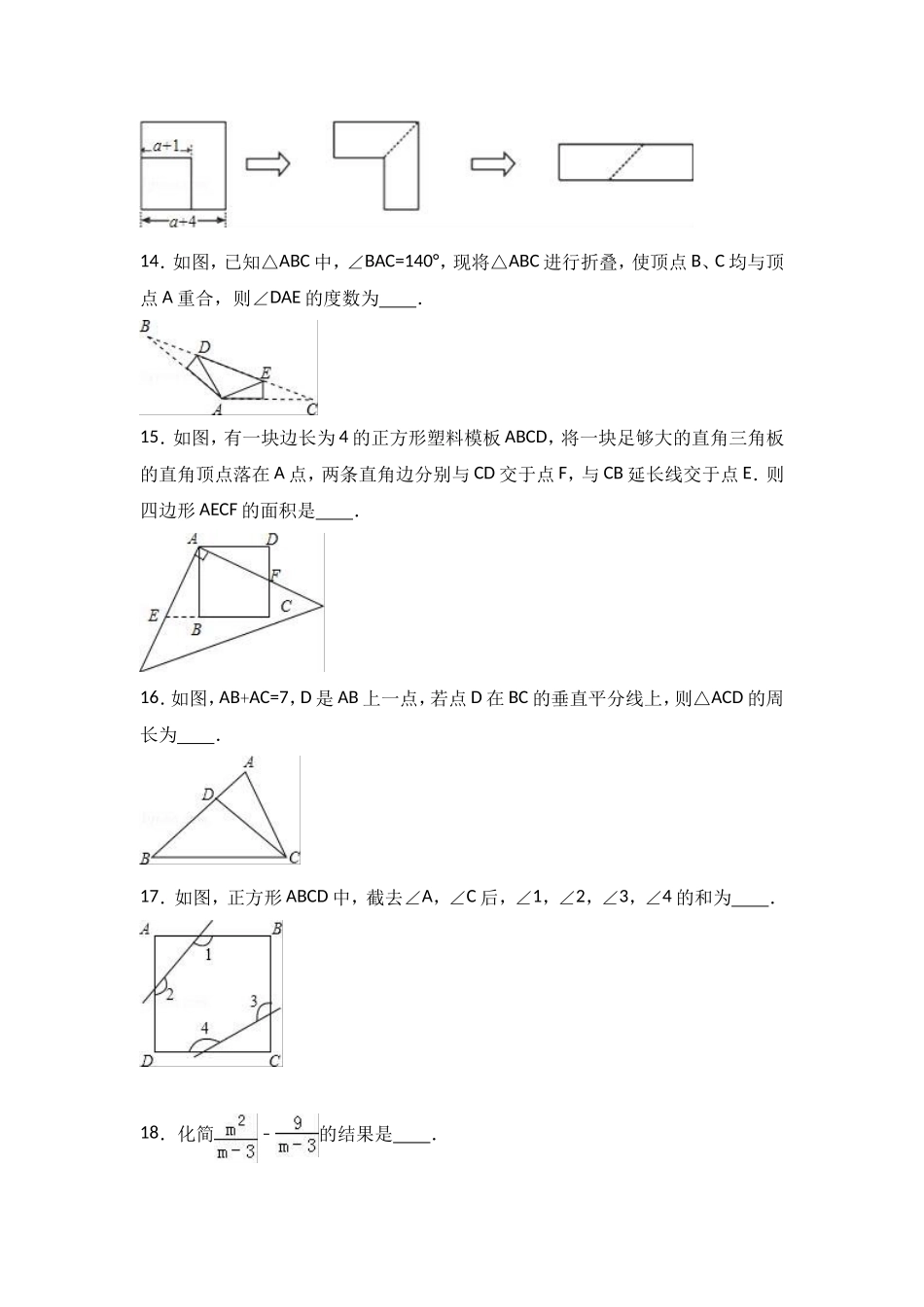
八年级(上)期末数学试卷一、精心选一选(本题共10个小题,每小题2分,共20分,在每小题给出的四个选项中,只有一项是符合要求的)1.下面四个图案中,是轴对称图形的是()A.B.C.D.2.若分式的值为0,则x的值为()A.﹣1B.0C.2D.﹣1或23.已知点P(1,a)与Q(b,2)关于x轴成轴对称,则ab﹣的值为()A.﹣1B.1C.﹣3D.34.如图,△ACB≌△ACB′′,∠BCB=30°′,则∠ACA′的度数为()A.20°B.30°C.35°D.40°5.下列各式由左边到右边的变形中,属于分解因式的是()A.a(x+y)=ax+ayB.x24x﹣+4=x(x4﹣+)C.10x25x=5x﹣(2x1﹣)D.x216﹣+3x=(x+4)(x4﹣)+3x6.如果一个多边形的每个内角都相等,且内角和为1800度,那么这个多边形的一个外角是()A.30°B.36°C.60°D.72°7.化简的结果是()A.mB.C.﹣mD.﹣8.用一条长为16cm的细绳围成一个等腰三角形,若其中有一边的长为4cm,则该等腰三角形的腰长为()A.4cmB.6cmC.4cm或6cmD.4cm或8cm9.若3x=4,3y=6,则3x2y﹣的值是()A.B.9C.D.310.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为()A.15°B.22.5°C.30°D.45°二、细心填一填(本大题共8个小题,每小题3分,共24分)11.一粒芝麻约有0.000002千克,0.000002用科学记数法表示为千克.12.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为.13.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为.14.如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,则∠DAE的度数为.15.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是.16.如图,AB+AC=7,D是AB上一点,若点D在BC的垂直平分线上,则△ACD的周长为.17.如图,正方形ABCD中,截去∠A,∠C后,∠1,∠2,∠3,∠4的和为.18.化简﹣的结果是.三、解答题(本大题共6小题,共56分)19.计算:(1)x(4x+3y)﹣(2x+y)(2xy﹣)(2)÷(1+)20.分解因式:(mn﹣)(3m+n)2+(m+3n)2(nm﹣)21.解方程:(1)+3=(2)﹣=1.22.如图是由16个小正方形组成的正方形网格图...