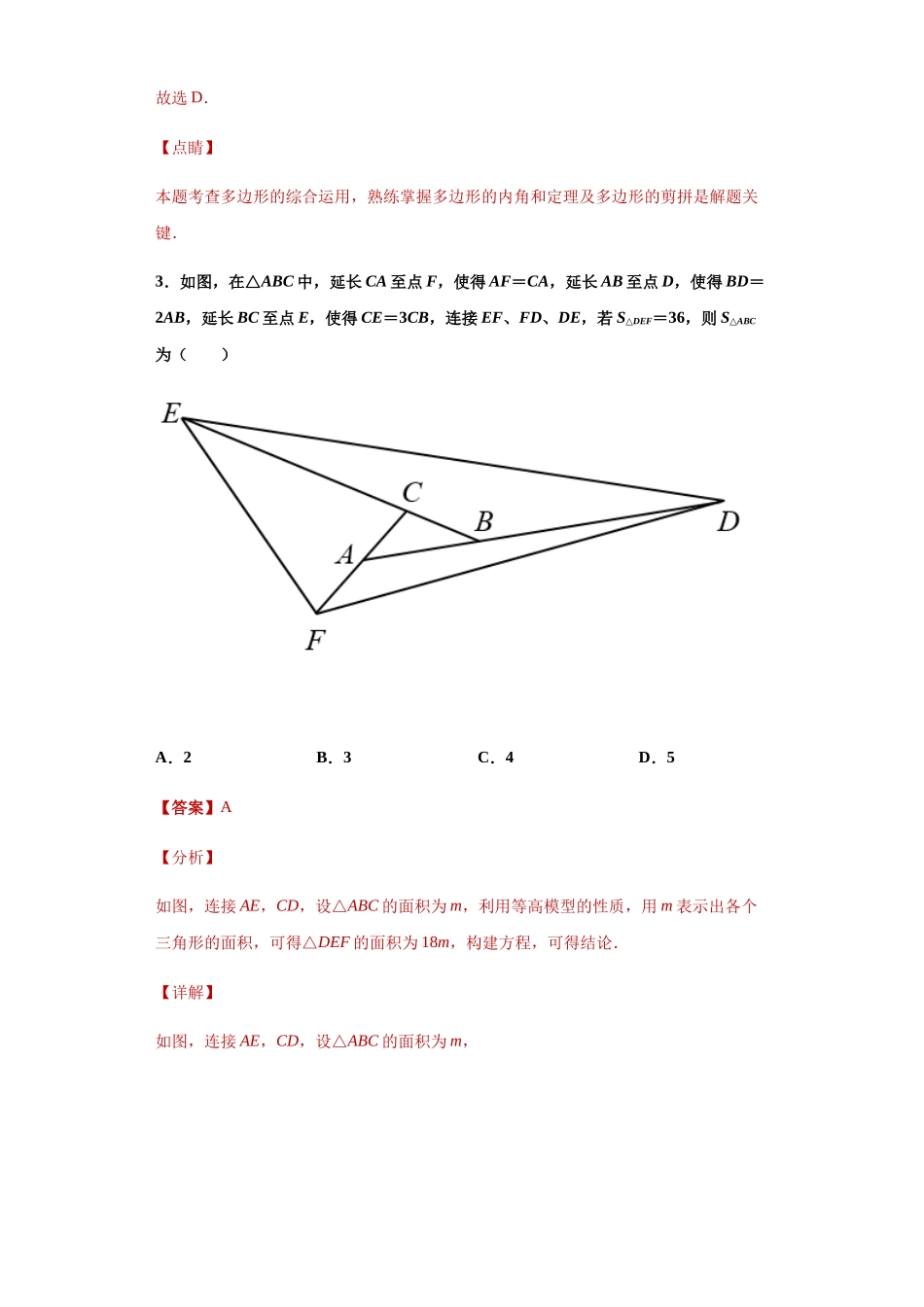
第一学期人教版八年级数学期中模拟卷二(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题(共30分)1.如图,在中,,.若是的高,与角平分线相交于点,则的度数为()A.130°B.70°C.110°D.100°【答案】A【分析】根据∠BOE=∠BAO+∠ABO,求出∠BAO,∠ABO即可,根据补角的定义求得.【详解】解: ∠BAC=80°,AE平分∠BAC,∴∠BAE=∠BAC=40°, BF⊥AC,∴∠BFA=90°,∴∠ABF=10°,∴∠BOE=∠BAO+∠ABO=40°+10°=50°,∴=130°,更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com故选:A【点睛】本题考查三角形内角和定理,三角形的角平分线,高的性质等知识,解题的关键是熟练掌握基本知识属于中考常考题型.2.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是()A.10或11B.11或12或13C.11或12D.10或11或12【答案】D【分析】首先求出截角后的多边形边数,然后再根据切去的位置求原来的多边形边数.【详解】解:设截角后的多边形边数为n,则有:(n-2)×180°=1620°,解得:n=11,如图1,从角两边的线段中间部分切去一个角后,在原边数基础上增加一条边,为12边形;如图2,从角的一边中间部分,另一边与另一顶点连结点处截取一个角,边数不增也不减,是11边形;;如图3,从另外两个顶点处切去一个角,边数减少1为10边形∴可得原来多边形的边数为10或11或12:故选D.【点睛】本题考查多边形的综合运用,熟练掌握多边形的内角和定理及多边形的剪拼是解题关键.3.如图,在△ABC中,延长CA至点F,使得AF=CA,延长AB至点D,使得BD=2AB,延长BC至点E,使得CE=3CB,连接EF、FD、DE,若S△DEF=36,则S△ABC为()A.2B.3C.4D.5【答案】A【分析】如图,连接AE,CD,设△ABC的面积为m,利用等高模型的性质,用m表示出各个三角形的面积,可得△DEF的面积为18m,构建方程,可得结论.【详解】如图,连接AE,CD,设△ABC的面积为m,更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.comBD=2AB,S△BCD=2S△ABC=2m,S△ACD=S△BCD+S△ABC=3m,AC=AF,S△ADF=S△ACD=3m,EC=3BC,S△ECA==3S△ABC=...