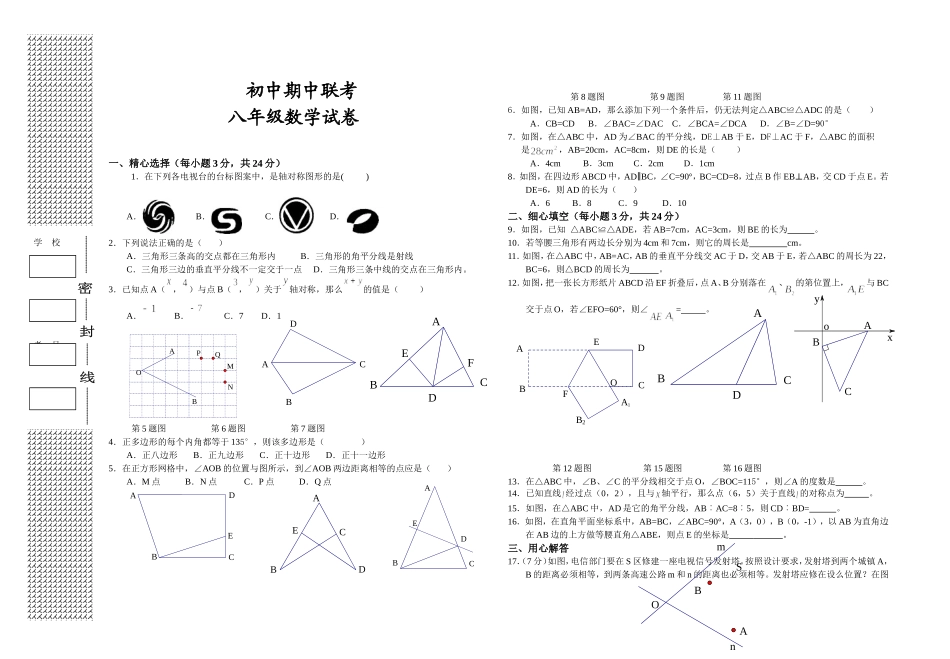
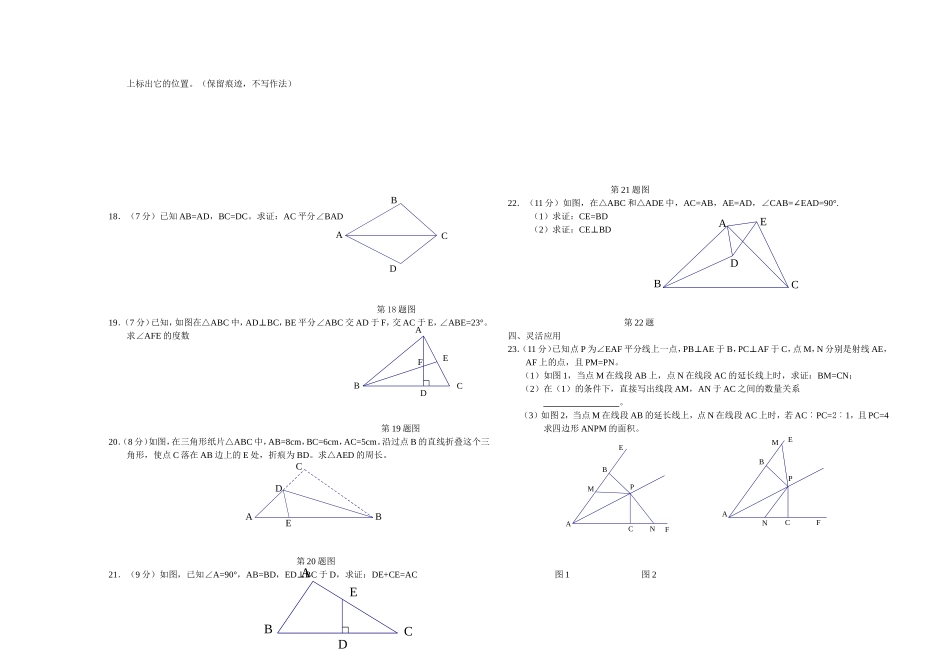
学校班级姓名考号初中期中联考八年级数学试卷一、精心选择(每小题3分,共24分)1.在下列各电视台的台标图案中,是轴对称图形的是()A.B.C.D.2.下列说法正确的是()A.三角形三条高的交点都在三角形内B.三角形的角平分线是射线C.三角形三边的垂直平分线不一定交于一点D.三角形三条中线的交点在三角形内。3.已知点A(,)与点B(,)关于轴对称,那么的值是()A.B.C.7D.1第5题图第6题图第7题图4.正多边形的每个内角都等于135°,则该多边形是()A.正八边形B.正九边形C.正十边形D.正十一边形5.在正方形网格中,∠AOB的位置与图所示,到∠AOB两边距离相等的点应是()A.M点B.N点C.P点D.Q点第8题图第9题图第11题图6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=90°7.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是,AB=20cm,AC=8cm,则DE的长是()A.4cmB.3cmC.2cmD.1cm8.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E。若DE=6,则AD的长为()A.6B.8C.9D.10二、细心填空(每小题3分,共24分)9.如图,已知△ABC≌△ADE,若AB=7cm,AC=3cm,则BE的长为。10.若等腰三角形有两边长分别为4cm和7cm,则它的周长是cm。11.如图,在△ABC中,AB=AC,AB的垂直平分线交AC于D,交AB于E,若△ABC的周长为22,BC=6,则△BCD的周长为。12.如图,把一张长方形纸片ABCD沿EF折叠后,点A、B分别落在、的第位置上,与BC交于点O,若∠EFO=60°,则∠=。第12题图第15题图第16题图13.在△ABC中,∠B、∠C的平分线相交于点O,∠BOC=115°,则∠A的度数是。14.已知直线经过点(0,2),且与轴平行,那么点(6,5)关于直线的对称点为。15.如图,在△ABC中,AD是它的角平分线,AB︰AC=8︰5,则CD︰BD=。16.如图,在直角平面坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0,-1),以AB为直角边在AB边的上方做等腰直角△ABE,则点E的坐标是。三、用心解答17.(7分)如图,电信部门要在S区修建一座电视信号发射塔。按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等。发射塔应修在设么位置?在图QOMNPBAB2A1OFEDCBADCBACBAoyxOSnmABEDCBAEDCBADABCFEDCBAEDCBA上标出它的位置。(保留痕迹,不写作法)18.(7分)已知AB=AD,BC=DC。求证:AC平分∠B...