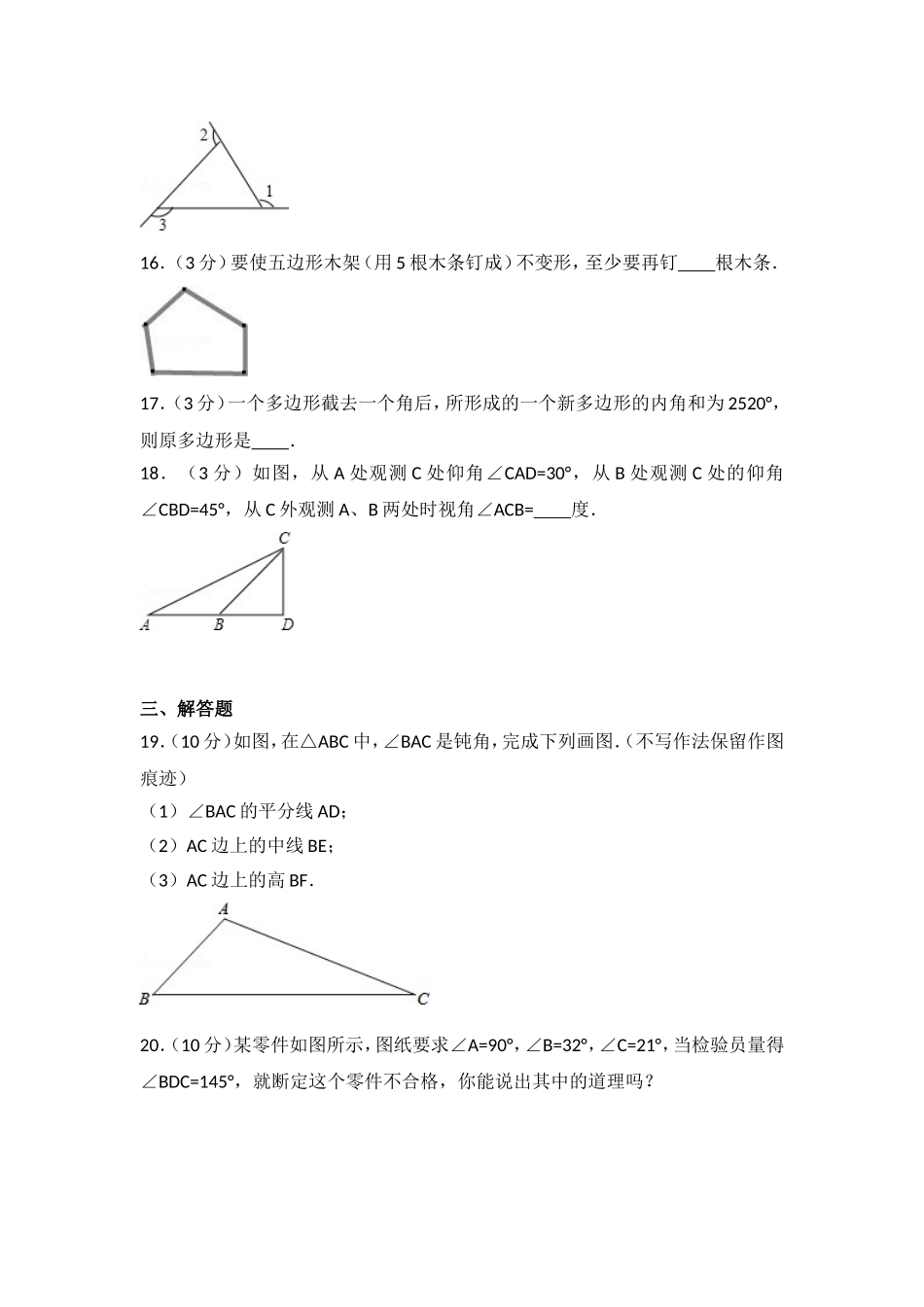
八年级(上)第一次月考数学试卷一.选择题(10小题,共30分)1.(3分)以下列各组线段为边,能组成三角形的是()A.3cm,4cm,5cmB.4cm,6cm,10cmC.1cm,1cm,3cmD.3cm,4cm,9cm2.(3分)已知等腰三角形的一边长等于4,一边长等于9,则它的周长为()A.22B.17C.17或22D.263.(3分)一个三角形的两边长分别为3和8,第三边长是一个偶数,则第三边的长不能为()A.6B.8C.10D.124.(3分)在如图中,正确画出AC边上高的是()A.B.C.D.5.(3分)如图,线段AD把△ABC分为面积相等的两部分,则线段AD是()A.三角形的角平分线B.三角形的中线C.三角形的高D.以上都不对6.(3分)适合条件∠A=∠B=∠C的三角形是()A.锐角三角形B.等边三角形C.钝角三角形D.直角三角形7.(3分)过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的边数是()A.8B.9C.10D.118.(3分)若一个多边形的内角和等于1080°,则这个多边形的边数是()A.9B.8C.7D.69.(3分)一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是()A.5B.6C.7D.810.(3分)三角形的一个外角是锐角,则此三角形的形状是()A.锐角三角形B.钝角三角形C.直角三角形D.无法确定11.(3分)n边形的每个外角都为24°,则边数n为()A.13B.14C.15D.1612.(3分)如图,∠A+∠B+∠C+∠D+∠E+∠F的和为()A.180°B.360°C.540°D.720°二、填空题(每小题3分,共30分)13.(3分)如图,共有个三角形.14.(3分)如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是.15.(3分)如图,∠1,∠2,∠3是△ABC的不同的三个外角,则∠1+∠2+∠3=度.16.(3分)要使五边形木架(用5根木条钉成)不变形,至少要再钉根木条.17.(3分)一个多边形截去一个角后,所形成的一个新多边形的内角和为2520°,则原多边形是.18.(3分)如图,从A处观测C处仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C外观测A、B两处时视角∠ACB=度.三、解答题19.(10分)如图,在△ABC中,∠BAC是钝角,完成下列画图.(不写作法保留作图痕迹)(1)∠BAC的平分线AD;(2)AC边上的中线BE;(3)AC边上的高BF.20.(10分)某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?21.(10分)如图,EB∥DC,∠C=∠E,请你说出∠A=∠ADE的理由.22...