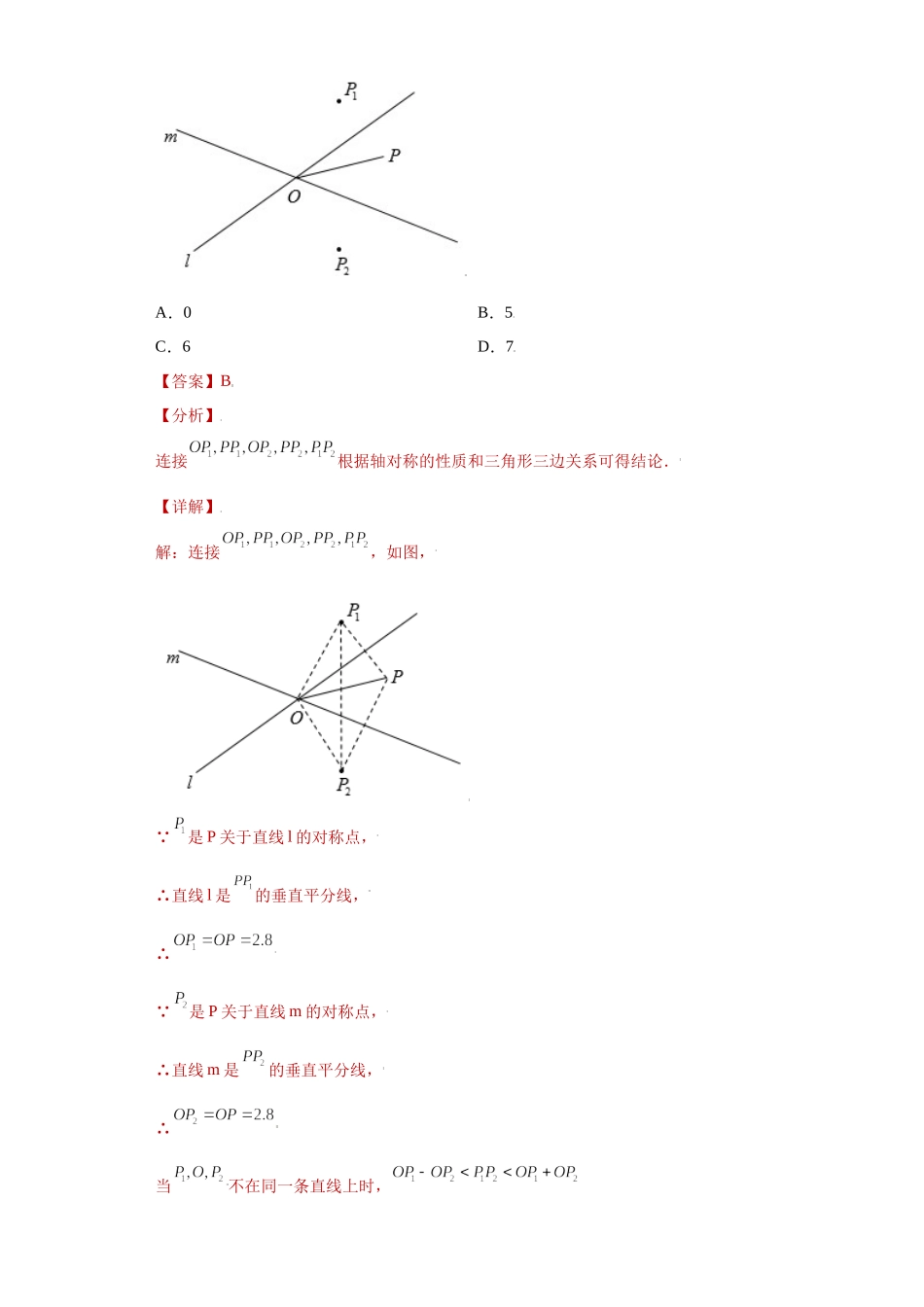
专题10推理能力课之轴对称综合重难点专练(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图为5×5的方格,其中有A、B、C三点,现有一点P在其它格点上,且A、B、C、P为轴对称图形,问共有几个这样的点P()A.5B.4C.3D.2【答案】B【分析】利用轴对称图形的性质得出符合题意的点即可.【详解】解:如图所示:A、B、C、P为轴对称图形,共有4个这样的点P.答案:B.【点睛】此题主要考查了利用轴对称设计图案,正确把握轴对称图形的定义是解题关键.2.是网格中的格点三角形(三角形的各顶点都在网格的交叉点上),如图建立直角坐标系,将该三角形先向下平移2个单位,然后再将平移后的图形沿y轴翻折,得到,则点B对应点的坐标为()更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.comA.B.C.D.【答案】A【分析】根据网格求出点B坐标,向下平移2个单位,点B的横坐标不变,纵坐标减2得对应点B1的坐标,再沿y轴翻折,横坐标变为相反数,纵坐标不变即可得出点B′(-4,3).【详解】解: 点B坐标为(4,5)向下平移2个单位,得点B对应点的坐标B1(4,5-2),即B1(4,3),再沿y轴翻折,点B′(-4,3),故选择A.【点睛】本题考查根据平面直角坐标系写出点的坐标,平移的性质,轴对称性质,掌握平面直角坐标系点的坐标构成,平移的性质,轴对称性质是解题关键.3.如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是()A.0B.5C.6D.7【答案】B【分析】连接根据轴对称的性质和三角形三边关系可得结论.【详解】解:连接,如图, 是P关于直线l的对称点,∴直线l是的垂直平分线,∴ 是P关于直线m的对称点,∴直线m是的垂直平分线,∴当不在同一条直线上时,更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com即当在同一条直线上时,故选:B【点睛】此题主要考查了轴对称变换,熟练掌握轴对称变换的性质是解答此题的关键4.如图,的角平分线与的垂直平分线交于点,垂足分别为,若,则的周长为()A.19B.28C.29D.38【答案】B【分析】连接BD、DC,证△BDE≌△CDF,可得CF=BE,根据角平分线性质可...