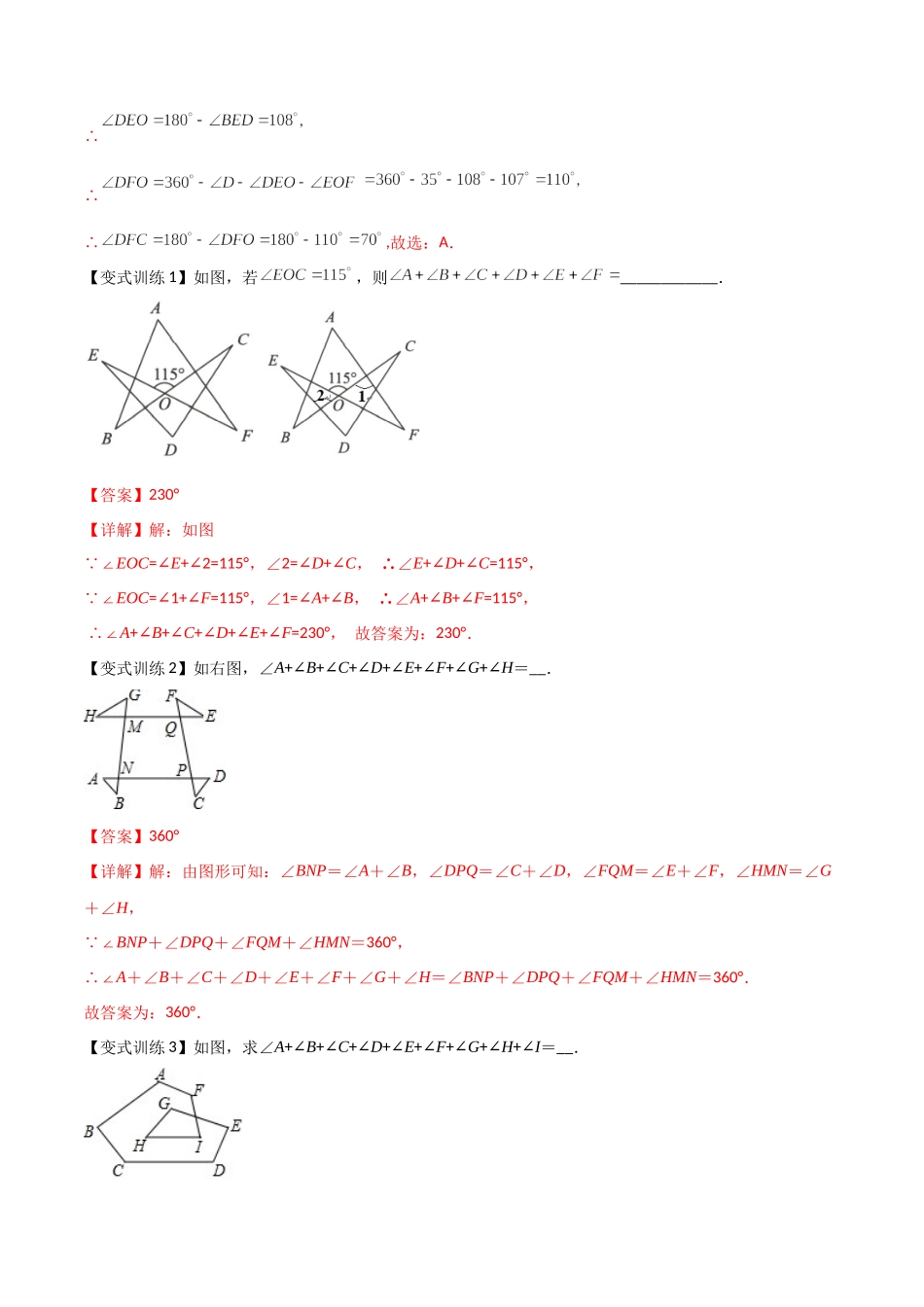
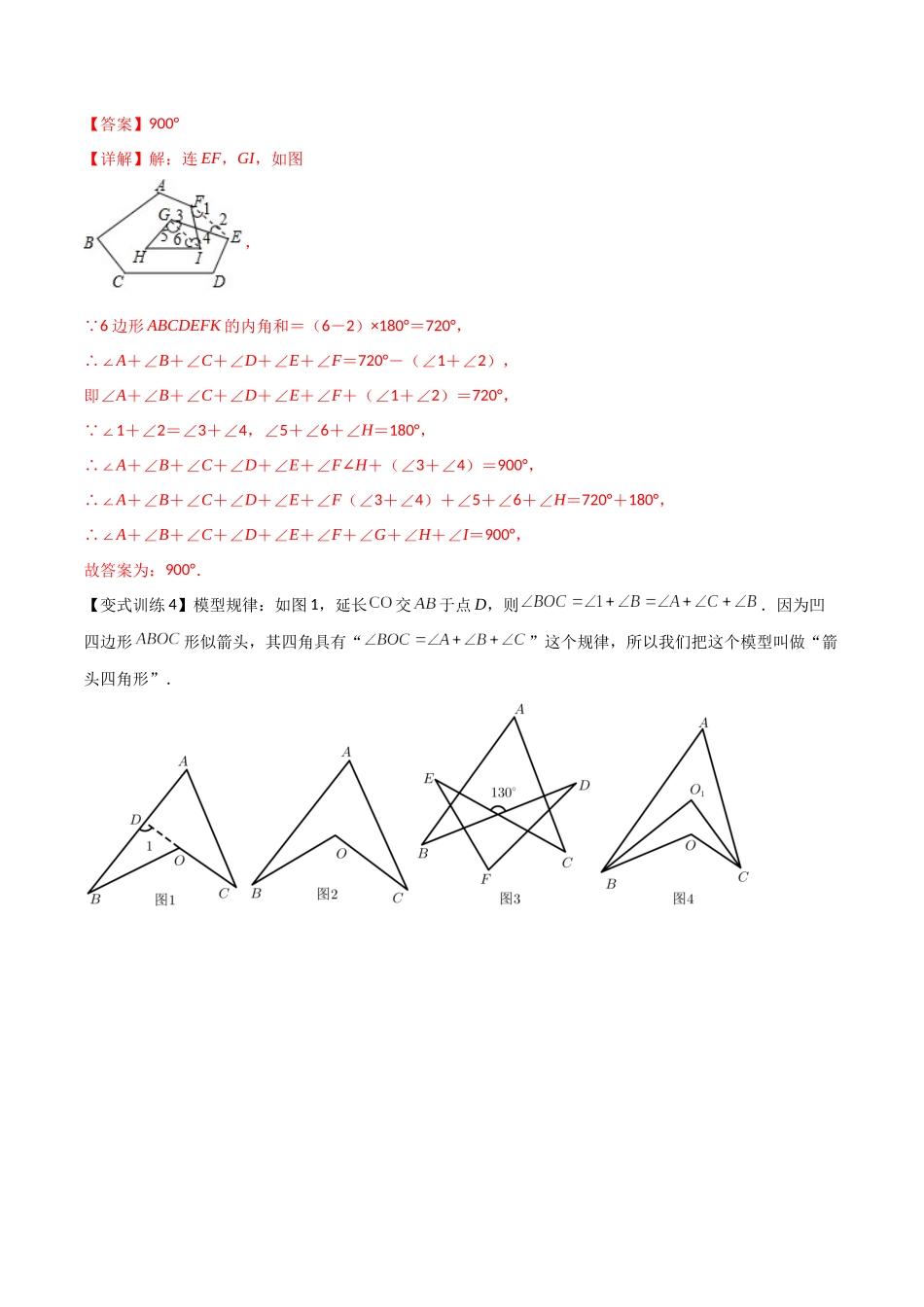
专题01三角形边或角关系的三种模型几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明角的数量关系,或者三角形的三边和差关系等,接来下我们针对这两个版块做出详细分析与梳理。类型一、燕尾角模型例1.在社会实践手工课上,小茗同学设计了一个形状如图所示的零件,如果,,那么的度数是().A.B.C.D.【答案】A【详解】延长BE交CF的延长线于O,连接AO,如图, ∴同理得 ∴ ∴∴∴,故选:A.【变式训练1】如图,若,则____________.【答案】230°【详解】解:如图 ∠EOC=∠E+2=115°∠,∠2=∠D+∠C,∴∠E+∠D+∠C=115°, ∠EOC=1+∠∠F=115°,∠1=∠A+∠B,∴∠A+∠B+∠F=115°,∴∠A+∠B+∠C+∠D+∠E+∠F=230°,故答案为:230°.【变式训练2】如右图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.【答案】360°【详解】解:由图形可知:∠BNP=∠A+∠B,∠DPQ=∠C+∠D,∠FQM=∠E+∠F,∠HMN=∠G+∠H, ∠BNP+∠DPQ+∠FQM+∠HMN=360°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=∠BNP+∠DPQ+∠FQM+∠HMN=360°.故答案为:360°.【变式训练3】如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=__.【答案】900°【详解】解:连EF,GI,如图,6 边形ABCDEFK的内角和=(6-2)×180°=720°,∴∠A+∠B+∠C+∠D+∠E+∠F=720°-(∠1+∠2),即∠A+∠B+∠C+∠D+∠E+∠F+(∠1+∠2)=720°,1 ∠+∠2=∠3+∠4,∠5+∠6+∠H=180°,∴∠A+∠B+∠C+∠D+∠E+∠F∠H+(∠3+∠4)=900°,∴∠A+∠B+∠C+∠D+∠E+∠F(∠3+∠4)+∠5+∠6+∠H=720°+180°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°,故答案为:900°.【变式训练4】模型规律:如图1,延长交于点D,则.因为凹四边形形似箭头,其四角具有“”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用(1)直接应用:①如图2,,则__________;②如图3,__________;(2)拓展应用:①如图4,、的2等分线(即角平分线)、交于点,已知,,则__________;②如图5,、分别为、的10等分线.它们的交点从上到下依次为、、、…、.已知,,则__________;③如图6,、的角平分线、交于点D,已知,则__________;④如图7,、的角平分线、交于点D,则、、之同的数量关系为__________.【答案】(1)①110;②260;(2)①85;②110;③142;④∠B-∠C+2∠D=0【详解】解:(1)...