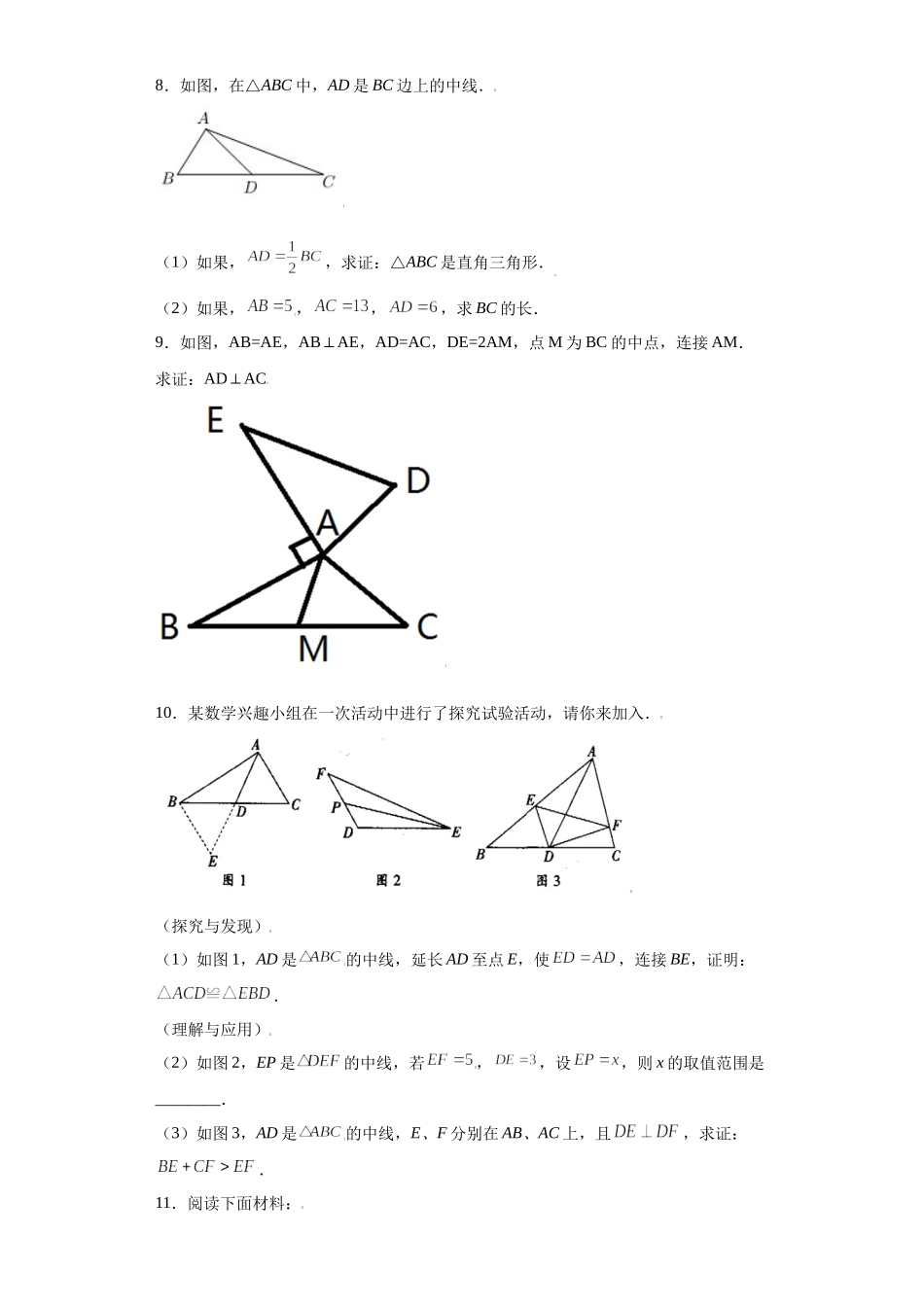
专题01模型方法课之倍长中线法重点练(原卷版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,在△ABC中,AB=5,AC=3,AD是BC边上的中线,AD的取值范围是()A.1<AD<6B.1<AD<4C.2<AD<8D.2<AD<42.如图,在中,为的中点,若.则的长不可能是()A.5B.7C.8D.93.如图,在四边形中,,,,,,点是的中点,则的长为().A.2B.C.D.3二、填空题4.如图,在中,是边上的中线,,,,则更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com_______.5.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF=__.三、解答题6.在ABC中,∠C=90°,AC>BC,D是AB的中点,E为直线AC上一动点,连接DE,过点D作DFDE⊥,交直线BC于点F,连接EF.(1)如图1,当点E是线段AC的中点时,AE=2,BF=1,求EF的长;(2)当点E在线段CA的延长线上时,依题意补全图形2,用等式表示AE,EF,BF之间的数量关系,并证明.7.如图,已知AD是的中线,过点B作BEAD⊥,垂足为E.若BE=6,求点C到AD的距离.8.如图,在△ABC中,AD是BC边上的中线.(1)如果,,求证:△ABC是直角三角形.(2)如果,,,,求BC的长.9.如图,AB=AE,ABAE⊥,AD=AC,DE=2AM,点M为BC的中点,连接AM.求证:ADAC⊥10.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.(探究与发现)(1)如图1,AD是的中线,延长AD至点E,使,连接BE,证明:.(理解与应用)(2)如图2,EP是的中线,若,,设,则x的取值范围是________.(3)如图3,AD是的中线,E、F分别在AB、AC上,且,求证:.11.阅读下面材料:更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com数学课上,老师给出了如下问题:如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.经过讨论,同学们得到以下思路:如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.完成下面问题:(1)这一思路的辅助线的作法是:.(2)请你给出一种不同...