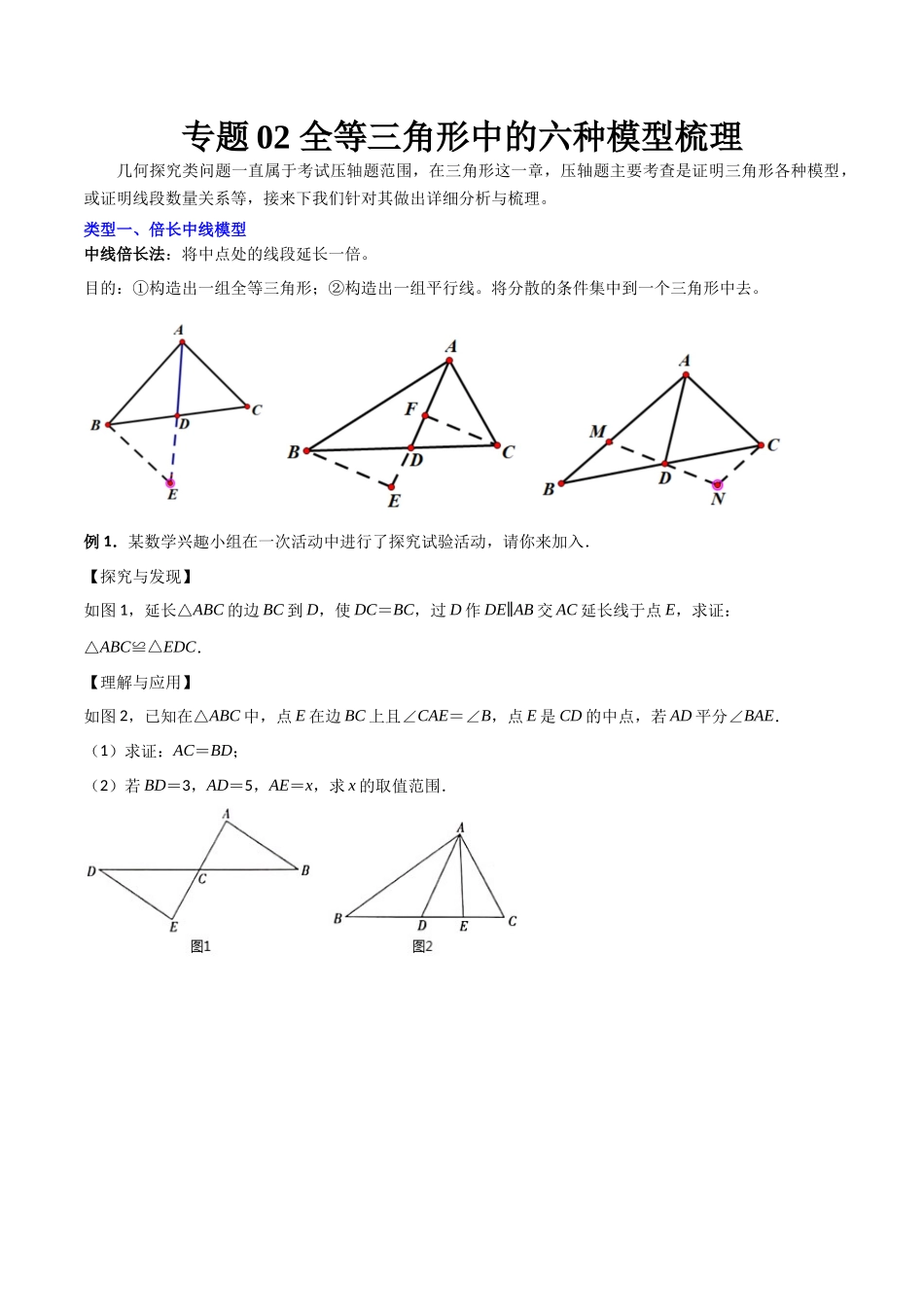
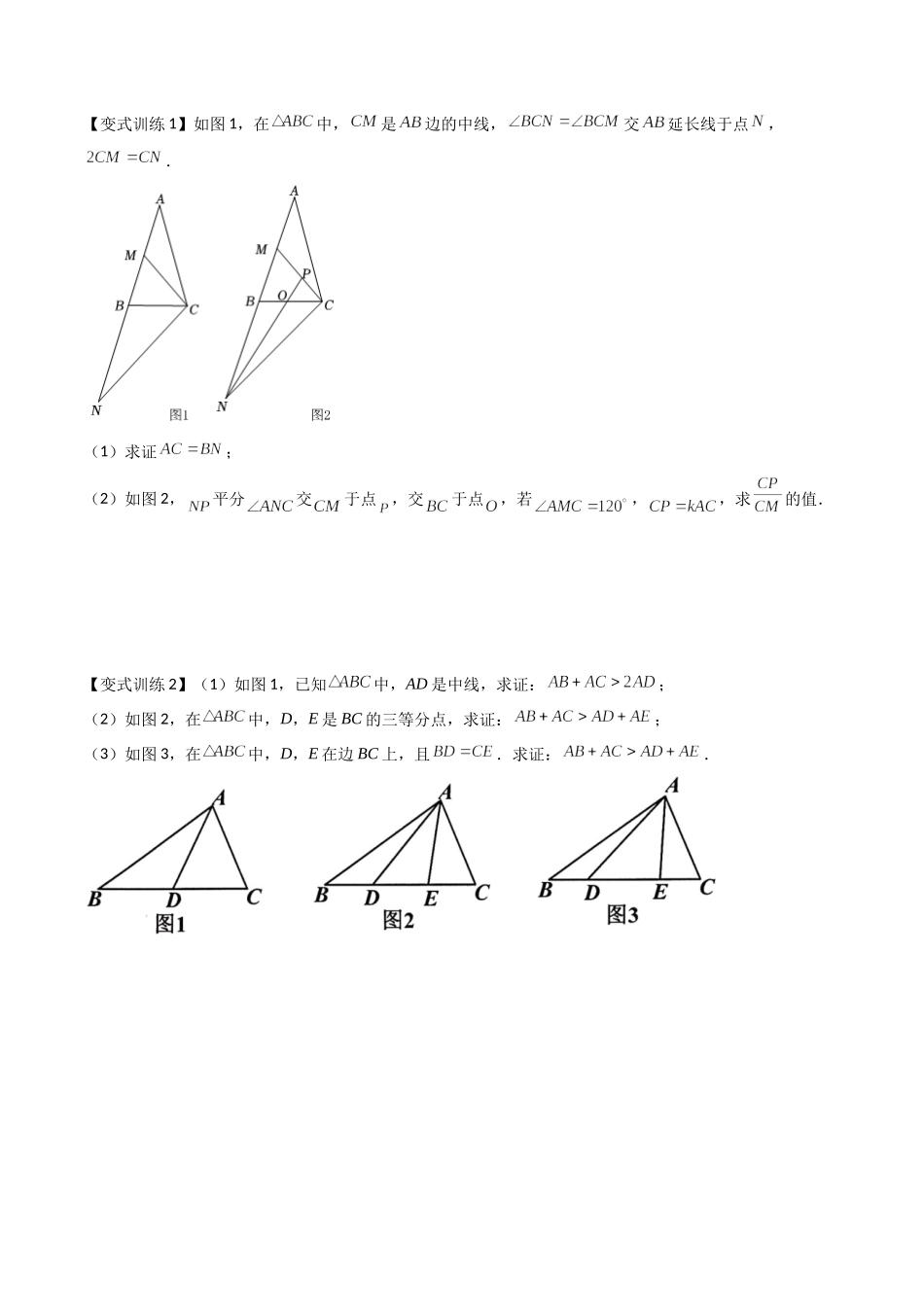
专题02全等三角形中的六种模型梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。类型一、倍长中线模型中线倍长法:将中点处的线段延长一倍。目的:①构造出一组全等三角形;②构造出一组平行线。将分散的条件集中到一个三角形中去。例1.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.【探究与发现】如图1,延长△ABC的边BC到D,使DC=BC,过D作DE∥AB交AC延长线于点E,求证:△ABC≌△EDC.【理解与应用】如图2,已知在△ABC中,点E在边BC上且∠CAE=∠B,点E是CD的中点,若AD平分∠BAE.(1)求证:AC=BD;(2)若BD=3,AD=5,AE=x,求x的取值范围.【变式训练1】如图1,在中,是边的中线,交延长线于点,.(1)求证;(2)如图2,平分交于点,交于点,若,,求的值.【变式训练2】(1)如图1,已知中,AD是中线,求证:;(2)如图2,在中,D,E是BC的三等分点,求证:;(3)如图3,在中,D,E在边BC上,且.求证:.【变式训练3】在中,点为边中点,直线绕顶点旋转,直线于点.直线于点,连接,.(1)如图1,若点,在直线的异侧,延长交于点.求证:.(2)若直线绕点旋转到图2的位置时,点,在直线的同侧,其它条件不变,此时,,,求的长度.(3)若过点作直线于点.试探究线段、和的关系.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)例.在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?答:.(请在空格内填“一定成立”“不一定成立”或“一定不成立”).(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.【变式训练1】如图,在四边形中,,点E、F分别在直线、上,且.(1)当点E、F分别在边、上时(如图1),请说明的理由.(2)当点E、F分别在边、延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出、、之间的数量关系,并说明理由.【变式训练2】(1)阅读理解:问题:如图1,在四边形中,对角线平分,.求证:.思考:...