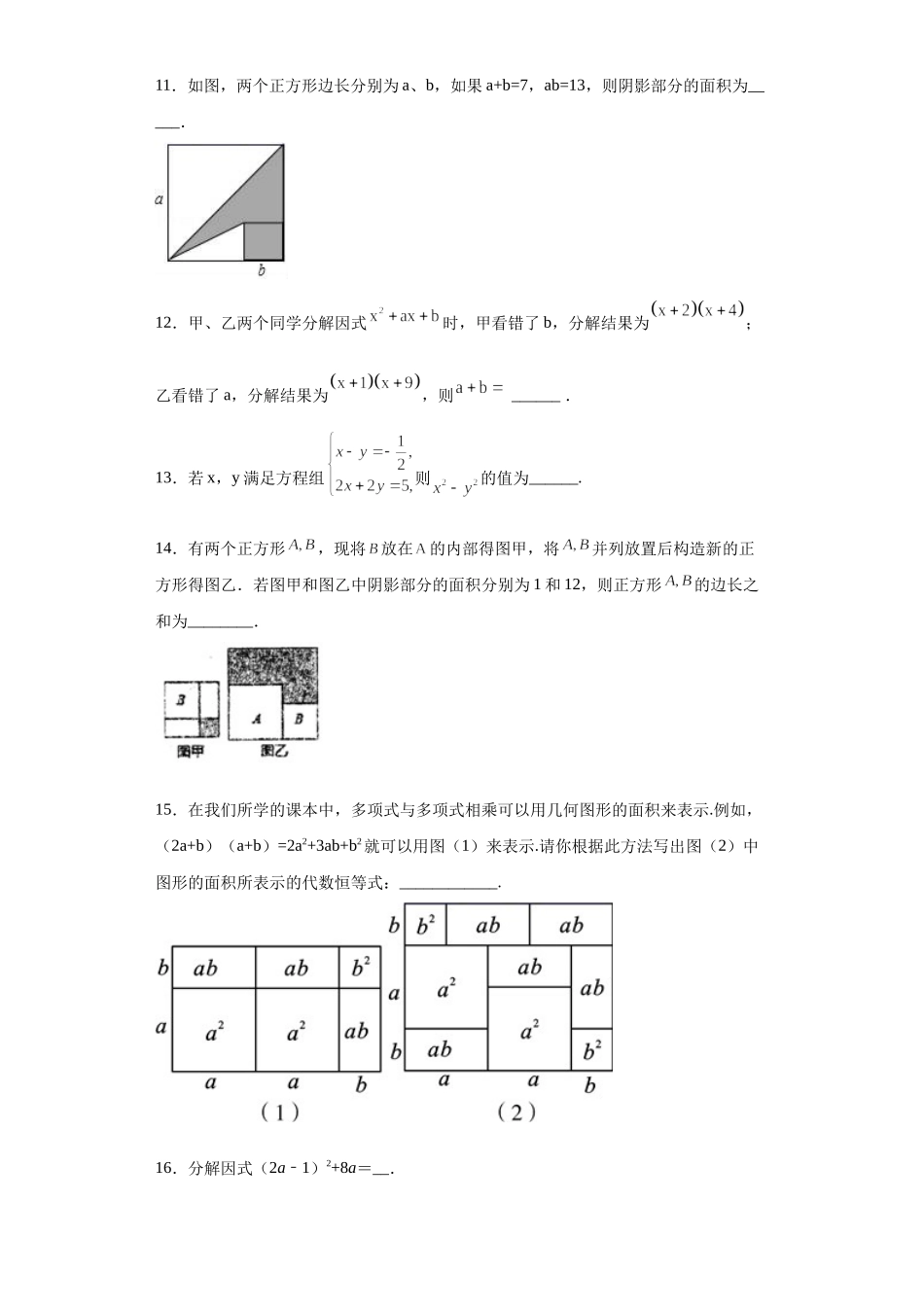
专题04整式的乘法与因式分解单元综合提优专练(原卷版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列从左到右的变形中是因式分解的有()x①2y﹣21=(x+y)(xy)1﹣﹣﹣;x②3+x=x(x2+1);(xy)③﹣2=x22xy+y﹣2;x④29y﹣2=(x+3y)(x3y).﹣A.1个B.2个C.3个D.4个2.下列等式从左到右的变形是因式分解的是()A.2x(x+3)=2x2+6xB.24xy2=3x•8y2C.x2+2xy+y2+1=(x+y)2+1D.x2﹣y2=(x+y)(x﹣y)3.已知A=﹣4x2,B是多项式,在计算B+A时,小马虎同学把B+A看成了B•A,结果得32x516x﹣4,则B+A为()A.﹣8x3+4x2B.﹣8x3+8x2C.﹣8x3D.8x34.图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是()A.2mnB.(m+n)2C.(m-n)2D.m2-n25.观察下列各式及其展开式:(a+b)2=a2+2ab+b2(a+b)3=a3+3a2b+3ab2+b3(a+b)4=a4+4a3b+6a2b2+4ab3+b4(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5…请你猜想(a+b)10的展开式第三项的系数是()A.36B.45C.55D.66更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com6.已知a2+a4=0﹣,那么代数式:a2(a+5)的值是()A.4B.8C.12D.167.下列因式分解正确的是()A.B.C.D.8.观察下列两个多项式相乘的运算过程:根据你发现的规律,若(x+a)(x+b)=x2-7x+12,则a,b的值可能分别是()A.,B.,4C.3,D.3,49.在边长为a的正方形中挖去一个边长为b的小正方形()(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证()A.B.C.D.10.因式分解,甲看错了a的值,分解的结果是,乙看错了b的值,分解的结果为,那么分解因式正确的结果为().A.B.C.D.二、填空题11.如图,两个正方形边长分别为a、b,如果a+b=7,ab=13,则阴影部分的面积为_____.12.甲、乙两个同学分解因式时,甲看错了b,分解结果为;乙看错了a,分解结果为,则______.13.若x,y满足方程组则的值为______.14.有两个正方形,现将放在的内部得图甲,将并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形的边长之和为________.15.在我...