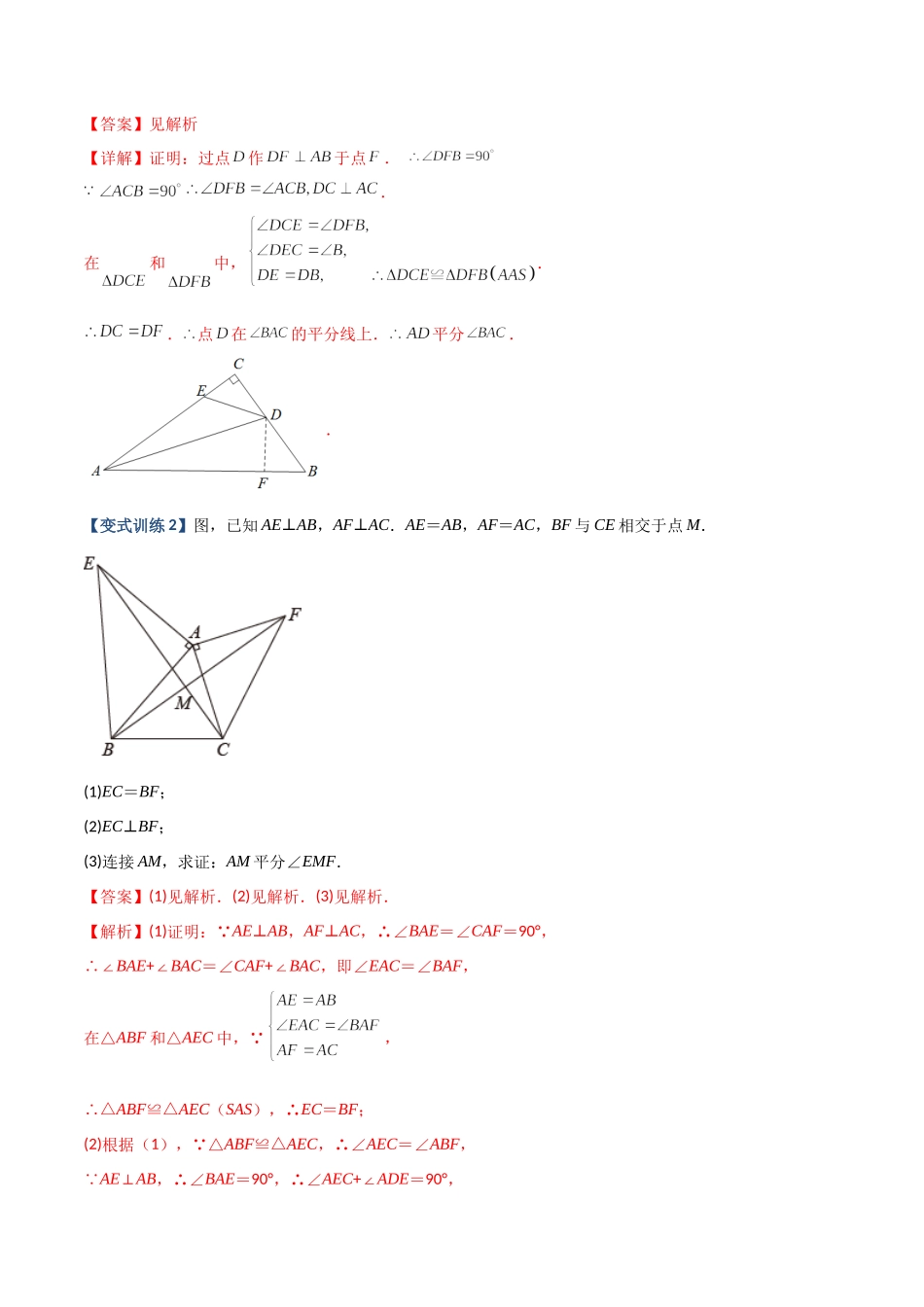
专题03与角平分线有关的辅助线的三种考法类型一、角平分线上的点向两边作垂线例1.如图,已知,P是的平分线上的任意一点,交于点D,于点E,如果,求的长.【答案】4cm【详解】如图,过点P作PF⊥OB于点F, OC平分∠AOB,PE⊥OA,∴PF=PE,∠EOP=∠DOP PDOA,∠AOB=30°,∴∠PDF=∠AOB=30°,∴∠DPO=∠EOP=∠DOP,∴PD=OD=8cm在RtPDF△中, ∠DFP=90°,∠FDP=30°∴PF=PD=4cm,∴PF=PE=4cm.【变式训练1】如图,中,,点分别在边,上,,.求证:平分.【答案】见解析【详解】证明:过点作于点..在和中,..点在的平分线上.平分..【变式训练2】图,已知AE⊥AB,AF⊥AC.AE=AB,AF=AC,BF与CE相交于点M.(1)EC=BF;(2)EC⊥BF;(3)连接AM,求证:AM平分∠EMF.【答案】(1)见解析.(2)见解析.(3)见解析.【解析】(1)证明: AE⊥AB,AF⊥AC,∴∠BAE=∠CAF=90°,∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF,在△ABF和△AEC中, ,∴△ABF≌△AEC(SAS),∴EC=BF;(2)根据(1), △ABF≌△AEC,∴∠AEC=∠ABF, AE⊥AB,∴∠BAE=90°,∴∠AEC+∠ADE=90°, ∠ADE=∠BDM(对顶角相等),∴∠ABF+∠BDM=90°,在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=180°90°﹣=90°,所以EC⊥BF.(3)作AP⊥CE于P,AQ⊥BF于Q.如图: △EAC≌△BAF,∴AP=AQ(全等三角形对应边上的高相等). AP⊥CE于P,AQ⊥BF于Q,∴AM平分∠EMF.【变式训练3】已知点C是∠MAN平分线上一点,∠BCD的两边CB、CD分别与射线AM、AN相交于B,D两点,且∠ABC+∠ADC=180°.过点C作CE⊥AB,垂足为E.(1)如图1,当点E在线段AB上时,求证:BC=DC;(2)如图2,当点E在线段AB的延长线上时,探究线段AB、AD与BE之间的等量关系;(3)如图3,在(2)的条件下,若∠MAN=60°,连接BD,作∠ABD的平分线BF交AD于点F,交AC于点O,连接DO并延长交AB于点G.若BG=1,DF=2,求线段DB的长.【答案】(1)见解析;(2)AD﹣AB=2BE,理由见解析;(3)3.【详解】(1)证明:如图1,过点C作CF⊥AD,垂足为F, AC平分∠MAN,CE⊥AB,CF⊥AD,∴CE=CF, ∠CBE+∠ADC=180°,∠CDF+∠ADC=180°,∴∠CBE=∠CDF,在△BCE和△DCF中,,∴△BCE≌△DCF(AAS)∴BC=DC;(2)解:AD﹣AB=2BE,理由如下:如图2,过点C作CF⊥AD,垂足为F, AC平分∠MAN,CE⊥AB,CF⊥AD,∴CE=CF,AE=AF, ∠ABC+∠ADC=180°,∠ABC+∠CBE=180°,∴∠CDF=∠CBE...